
La régression logistique a été utilisée dans les sciences biologiques au début du XXe siècle. Elle a ensuite été utilisée dans de nombreuses applications des sciences sociales. La régression logistique est utilisée lorsque la variable dépendante (cible) est catégorique.
Par exemple,
- Prédire si un courriel est un spam (1) ou (0)
- Si la tumeur est maligne (1) ou non (0)
Envisageons un scénario où nous devons classer si un courriel est un spam ou non. Si nous utilisons la régression linéaire pour ce problème, il est nécessaire de mettre en place un seuil sur la base duquel la classification peut être faite. Disons que si la classe réelle est maligne, la valeur continue prédite 0,4 et la valeur seuil est de 0,5, le point de données sera classé comme non malin, ce qui peut entraîner une conséquence grave en temps réel.
De cet exemple, on peut déduire que la régression linéaire ne convient pas au problème de classification. La régression linéaire n’est pas bornée, ce qui fait entrer en scène la régression logistique. Leur valeur est strictement comprise entre 0 et 1.
Régression logistique simple
(Code source complet : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb)
Modèle
Sortie = 0 ou 1
Hypothèse => Z = WX + B
hΘ(x) = sigmoïde (Z)
Sigmoïde. Fonction

Si ‘Z’ va à l’infini, Y(prédit) deviendra 1 et si ‘Z’ va à l’infini négatif, Y(prédit) deviendra 0.
Analyse de l’hypothèse
La sortie de l’hypothèse est la probabilité estimée. Elle est utilisée pour déduire avec quelle confiance la valeur prédite peut être la valeur réelle lorsqu’on donne une entrée X. Considérons l’exemple ci-dessous,
X = =
Sur la base de la valeur x1, disons que nous avons obtenu la probabilité estimée à 0,8. Cela nous indique qu’il y a 80% de chances qu’un email soit un spam.
Mathématiquement, cela peut s’écrire comme,

Ceci justifie le nom de » régression logistique « . Les données sont ajustées dans un modèle de régression linéaire, sur lequel agit ensuite une fonction logistique prédisant la variable dépendante catégorielle cible.
Types de régression logistique
1. Régression logistique binaire
La réponse catégorielle n’a que deux 2 issues possibles. Exemple : Spam ou pas
2. Régression logistique multinomiale
Trois catégories ou plus sans ordre. Exemple : Prédire quel aliment est préféré davantage (Veg, Non-Veg, Vegan)
3. Régression logistique ordinale
Trois catégories ou plus avec ordonnancement. Exemple : Classement des films de 1 à 5
Limite de décision
Pour prédire à quelle classe appartient une donnée, un seuil peut être défini. En fonction de ce seuil, la probabilité estimée obtenue est classée dans des classes.
Disons que si la valeur prédite ≥ 0,5, alors classer le courriel comme spam sinon comme non spam.
La limite de décision peut être linéaire ou non linéaire. L’ordre polynomial peut être augmenté pour obtenir une limite de décision complexe.
Fonction de coût
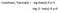
Pourquoi la fonction de coût qui a été utilisée pour le linéaire ne peut pas être utilisée pour le logistique ?
La régression linéaire utilise l’erreur quadratique moyenne comme fonction de coût. Si celle-ci est utilisée pour la régression logistique, alors elle sera une fonction non convexe des paramètres (thêta). La descente de gradient convergera vers le minimum global uniquement si la fonction est convexe.

Explication de la fonction de coût


Fonction de coût simplifiée

Pourquoi cette fonction de coût ?
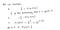
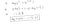
Cette fonction négative est due au fait que lorsque nous nous entraînons, nous devons maximiser la probabilité en minimisant la fonction de perte. Diminuer le coût augmentera le maximum de vraisemblance en supposant que les échantillons sont tirés d’une distribution identiquement indépendante.
Dérivation de la formule de l’algorithme de descente de gradient


Implémentation Python
def weightInitialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w,bdef sigmoid_activation(result):
final_result = 1/(1+np.exp(-result))
return final_result
def model_optimize(w, b, X, Y):
m = X.shape
#Prediction
final_result = sigmoid_activation(np.dot(w,X.T)+b)
Y_T = Y.T
cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result)))))
#
#Gradient calculation
dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T))
db = (1/m)*(np.sum(final_result-Y.T))
grads = {"dw": dw, "db": db}
return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations):
costs =
for i in range(no_iterations):
#
grads, cost = model_optimize(w,b,X,Y)
#
dw = grads
db = grads
#weight update
w = w - (learning_rate * (dw.T))
b = b - (learning_rate * db)
#
if (i % 100 == 0):
costs.append(cost)
#print("Cost after %i iteration is %f" %(i, cost))
#final parameters
coeff = {"w": w, "b": b}
gradient = {"dw": dw, "db": db}
return coeff, gradient, costsdef predict(final_pred, m):
y_pred = np.zeros((1,m))
for i in range(final_pred.shape):
if final_pred > 0.5:
y_pred = 1
return y_pred
Coût contre nombre_d’itérations

La précision d’entraînement et de test du système est de 100 %
Cette implémentation concerne la régression logistique binaire. Pour les données avec plus de 2 classes, la régression softmax doit être utilisée.
Ce post est éducatif et inspiré du cours d’apprentissage profond du Prof. Andrew Ng.
Code complet : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb