Il existe différents types de singularités, chacune avec des caractéristiques physiques différentes qui ont des caractéristiques pertinentes pour les théories dont elles ont émergé à l’origine, comme la forme différente des singularités, conique et courbe. On a également émis l’hypothèse qu’elles se produisent sans Horizons d’événements, structures qui délimitent une section de l’espace-temps d’une autre dans laquelle les événements ne peuvent pas affecter au-delà de l’horizon ; on les appelle nus.
Edit conique
Une singularité conique se produit lorsqu’il y a un point où la limite de chaque quantité invariante de difféomorphisme est finie, auquel cas l’espace-temps n’est pas lisse au point de la limite elle-même. Ainsi, l’espace-temps ressemble à un cône autour de ce point, où la singularité est située à l’extrémité du cône. La métrique peut être finie partout où le système de coordonnées est utilisé.
Un exemple d’une telle singularité conique est une corde cosmique et un trou noir de Schwarzschild.
CourbureEdit
Les résolutions des équations de la relativité générale ou d’une autre théorie de la gravité (comme la supergravité) aboutissent souvent à la rencontre de points où la métrique explose à l’infini. Cependant, beaucoup de ces points sont tout à fait réguliers, et les infinis sont simplement le résultat de l’utilisation d’un système de coordonnées inapproprié à ce point. Pour tester l’existence d’une singularité en un point donné, il faut vérifier si, à cet endroit, les quantités invariantes par difféomorphisme (c’est-à-dire les scalaires) deviennent infinies. De telles quantités sont les mêmes dans tous les systèmes de coordonnées, donc ces infinités ne vont pas « disparaître » par un changement de coordonnées.
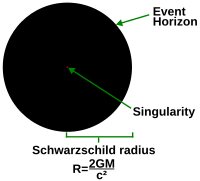
Un exemple est la solution de Schwarzschild qui décrit un trou noir non rotatif et non chargé. Dans les systèmes de coordonnées pratiques pour travailler dans des régions éloignées du trou noir, une partie de la métrique devient infinie à l’horizon des événements. Cependant, l’espace-temps à l’horizon des événements est régulier. Cette régularité devient évidente lorsqu’on passe à un autre système de coordonnées (comme les coordonnées de Kruskal), où la métrique est parfaitement lisse. En revanche, au centre du trou noir, où la métrique devient également infinie, les solutions suggèrent l’existence d’une singularité. L’existence de la singularité peut être vérifiée en notant que le scalaire de Kretschmann, étant le carré du tenseur de Riemann c’est-à-dire R μ ν ρ σ R μ ν ρ σ {\displaystyle R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }}.

, qui est invariante par difféomorphisme, est infinie.
Alors que dans un trou noir non rotatif, la singularité se produit en un seul point dans les coordonnées du modèle, appelé « singularité ponctuelle », dans un trou noir rotatif, également connu sous le nom de trou noir de Kerr, la singularité se produit sur un anneau (une ligne circulaire), appelé « singularité annulaire ». Une telle singularité peut aussi théoriquement devenir un trou de ver.
Plus généralement, un espace-temps est considéré comme singulier s’il est géodésiquement incomplet, ce qui signifie qu’il existe des particules en chute libre dont le mouvement ne peut être déterminé au-delà d’un temps fini, étant après le point d’atteinte de la singularité. Par exemple, tout observateur se trouvant à l’intérieur de l’horizon des événements d’un trou noir non rotatif tomberait en son centre dans un laps de temps fini. La version classique du modèle cosmologique du Big Bang contient une singularité causale au début du temps (t=0), où toutes les géodésiques temporelles n’ont aucune extension dans le passé. L’extrapolation vers l’arrière jusqu’à cet hypothétique temps 0 donne un univers avec toutes les dimensions spatiales de taille zéro, une densité infinie, une température infinie et une courbure infinie de l’espace-temps.
Singularité nueEdit
Jusqu’au début des années 1990, on croyait généralement que la relativité générale cachait chaque singularité derrière un horizon des événements, rendant les singularités nues impossibles. C’est ce qu’on appelle l’hypothèse de la censure cosmique. Cependant, en 1991, les physiciens Stuart Shapiro et Saul Teukolsky ont réalisé des simulations informatiques d’un plan de poussière en rotation qui ont montré que la relativité générale pouvait autoriser des singularités « nues ». On ignore à quoi ressembleraient réellement ces objets dans un tel modèle. On ne sait pas non plus si les singularités apparaîtraient toujours si les hypothèses simplificatrices utilisées pour réaliser la simulation étaient supprimées. Cependant, on suppose que la lumière entrant dans une singularité verrait de la même manière ses géodésiques se terminer, ce qui ferait ressembler la singularité nue à un trou noir.
Des horizons des événements disparus existent dans la métrique de Kerr, qui est un trou noir en rotation dans le vide, si le moment cinétique ( J {\displaystyle J}

) est suffisamment élevé. En transformant la métrique de Kerr en coordonnées Boyer-Lindquist, on peut montrer que la coordonnée (qui n’est pas le rayon) de l’horizon des événements est, r ± = μ ± ( μ 2 – a 2 ) 1 / 2 {\displaystyle r_{\pm }=\mu \pm (\mu ^{2}-a^{2})^{1/2}}.

, où μ = G M / c 2 {\displaystyle \mu =GM/c^{2}}

, et a = J / M c {\displaystyle a=J/Mc}

. Dans ce cas, « les horizons des événements disparaissent » signifie lorsque les solutions sont complexes pour r ± {\displaystyle r_{\pm }}.

, ou μ 2 < a 2 {\displaystyle \mu ^{2}<a^{2}}.

. Cependant, cela correspond à un cas où J {\displaystyle J}

dépasse G M 2 / c {\displaystyle GM^{2}/c}

(ou en unités de Planck, J > M 2 {\displaystyle J>M^{2}}.

), c’est-à-dire que le spin dépasse ce qui est normalement considéré comme la limite supérieure de ses valeurs physiquement possibles.

) est suffisamment élevée. Dans cette métrique, on peut montrer que les singularités se produisent à r ± = μ ± ( μ 2 – q 2 ) 1 / 2 {\displaystyle r_{\pm }=\mu \pm (\mu ^{2}-q^{2})^{1/2}}.

, où μ = G M / c 2 {\displaystyle \mu =GM/c^{2}

, et q 2 = G Q 2 / ( 4 π ϵ 0 c 4 ) {\displaystyle q^{2}=GQ^{2}/(4\pi \epsilon _{0}c^{4})}

. Parmi les trois cas possibles pour les valeurs relatives de μ {\displaystyle \mu }.

et de q {\displaystyle q}.

, le cas où μ 2 < q 2 {\displaystyle \mu ^{2}<q^{2}}.

cause les deux r ± {\displaystyle r_{\pm }}

sont complexes. Cela signifie que la métrique est régulière pour toutes les valeurs positives de r {\displaystyle r}.

, ou en d’autres termes, la singularité n’a pas d’horizon des événements. Cependant, cela correspond à un cas où Q / 4 π ϵ 0 {\displaystyle Q/{\sqrt {4\pi \epsilon _{0}}}}}.

dépasse M G {\displaystyle M{\sqrt {G}}

(ou en unités de Planck, Q > M {\displaystyle Q>M}

), c’est-à-dire que la charge dépasse ce qui est normalement considéré comme la limite supérieure de ses valeurs physiquement possibles. En outre, les trous noirs astrophysiques réels ne devraient pas posséder de charge appréciable.
Un trou noir possédant la plus faible M {\displaystyle M}

valeur compatible avec son J {\displaystyle J}.

et Q {\displaystyle Q}

et les limites notées ci-dessus, c’est-à-dire celui qui est juste au point de perdre son horizon des événements, est qualifié d’extrémal.