Vous vous demandez peut-être à quoi correspondent toutes ces sommes de carrés. C’est peut-être ce qui vous a amené ici en premier lieu. Eh bien, elles sont les déterminants d’une bonne régression linéaire. Ce tutoriel est basé sur le cadre de l’ANOVA que vous avez peut-être déjà entendu.
Avant de le lire, cependant, assurez-vous que vous ne confondez pas régression et corrélation. Si vous avez vérifié cela, nous pouvons passer directement à l’action.
Un petit aparté : vous voulez en savoir plus sur la régression linéaire ? Consultez nos vidéos explicatives Le modèle de régression linéaire. Représentation géométrique et Le modèle de régression linéaire simple.
SST, SSR, SSE : définition et formules
Il y a trois termes que nous devons définir. La somme des carrés totaux, la somme des carrés de régression et la somme des carrés d’erreur.

Qu’est-ce que la SST ?
La somme des carrés totaux, notée SST, correspond aux différences au carré entre la variable dépendante observée et sa moyenne. Vous pouvez considérer cela comme la dispersion des variables observées autour de la moyenne – un peu comme la variance dans les statistiques descriptives.
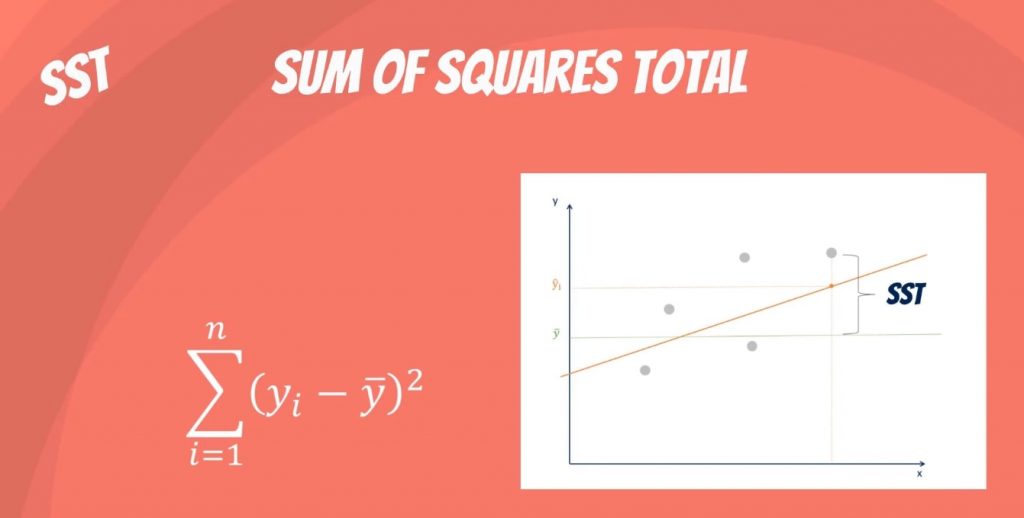
C’est une mesure de la variabilité totale de l’ensemble de données.
Note annexe : Il existe une autre notation pour la SST. Il s’agit de la TSS ou somme totale des carrés.
Qu’est-ce que la SSR ?
Le deuxième terme est la somme des carrés dus à la régression, ou SSR. Il s’agit de la somme des différences entre la valeur prédite et la moyenne de la variable dépendante. Pensez-y comme une mesure qui décrit la façon dont notre droite s’adapte aux données.

Si cette valeur de SSR est égale à la somme des carrés totale, cela signifie que notre modèle de régression capture toute la variabilité observée et qu’il est parfait. Une fois de plus, nous devons mentionner qu’une autre notation courante est ESS ou somme des carrés expliqués.
Qu’est-ce que la SSE ?
Le dernier terme est l’erreur de la somme des carrés, ou SSE. L’erreur est la différence entre la valeur observée et la valeur prédite.

Nous voulons généralement minimiser l’erreur. Plus l’erreur est petite, meilleur est le pouvoir d’estimation de la régression. Enfin, je dois ajouter qu’elle est également connue sous le nom de RSS ou somme résiduelle des carrés. Résiduelle comme dans : restante ou inexpliquée.
La confusion entre les différentes abréviations
Elle devient vraiment confuse car certaines personnes la désignent par SSR. On ne sait donc pas si l’on parle de la somme des carrés dus à la régression ou de la somme des carrés des résidus.

De toute façon, ni l’une ni l’autre ne sont universellement adoptées, donc la confusion demeure et il faudra vivre avec.
Simplement, retenez que les deux notations sont SST, SSR, SSE, ou TSS, ESS, RSS.

Il y a un conflit concernant les abréviations, mais pas sur le concept et son application. Donc, concentrons-nous sur ce point.
Comment sont-ils liés ?
Mathématiquement, SST = SSR + SSE.

Le raisonnement est le suivant : la variabilité totale de l’ensemble des données est égale à la variabilité expliquée par la droite de régression plus la variabilité inexpliquée, appelée erreur.

Sous réserve d’une variabilité totale constante, une erreur plus faible entraînera une meilleure régression. À l’inverse, une erreur plus élevée provoquera une régression moins puissante. Et c’est ce que vous devez retenir, quelle que soit la notation.
Étape suivante : Le R-carré
Bien, si vous ne savez pas pourquoi nous avons besoin de toutes ces sommes de carrés, nous avons l’outil qu’il vous faut. Le R-carré. Vous voulez en savoir plus ? Il suffit de plonger dans le tutoriel lié où vous comprendrez comment il mesure le pouvoir explicatif d’une régression linéaire !
***
Intéressé par un apprentissage plus poussé ? Vous pouvez faire passer vos compétences de bonnes à excellentes grâce à notre cours de statistiques.
Essayez gratuitement le cours de statistiques
Prochain tutoriel : Mesurer la variabilité avec le R-carré
.