Qu’est-ce que la symétrie ?
Regardez ces deux images de papillons. Quelle différence voyez-vous ?

Le premier papillon a exactement la même apparence des côtés gauche et droit tandis que le second papillon n’a pas la même apparence des côtés gauche et droit.
Les images qui peuvent être divisées en moitiés identiques sont dites symétriques. Les images qui ne peuvent pas être divisées en moitiés identiques sont asymétriques.
Vous avez dû voir les objets symétriques suivants dans votre environnement :

Ligne de symétrie
Toute ligne divisant une forme en deux parties telles que les deux parties sont identiques est appelée ligne de symétrie. On dit aussi que ces parties sont symétriques l’une de l’autre.
Par exemple, l’image ci-dessous montre une ligne de symétrie qui divise la forme à contour rouge en deux parties qui sont exactement les mêmes.


Sur la base des exemples ci-dessus, nous obtenons les observations suivantes :
-
Les côtés de l’image divisés par la ligne de symétrie, doivent être identiques.
-
Si nous plions le papier (sur lequel l’image est dessinée) le long de la ligne de symétrie, chaque partie de l’image recouvrira complètement l’autre partie.
Les observations ci-dessus nous aideront à trouver la ligne de symétrie dans n’importe quelle forme.
Exemple 1 : Laquelle des formes suivantes n’a pas de ligne de symétrie ?

Solution :
Si nous plions les deux papiers de haut en bas comme indiqué en A1 et B1, nous obtenons une ligne de symétrie en A mais pas en B. Si nous plions les deux papiers de gauche à droite comme indiqué en A2 et B2, nous n’obtenons aucune ligne de symétrie en A et B.

Formes avec plus d’une ligne de symétrie
Peut-on avoir plus d’une ligne de symétrie ? La réponse est oui. Le tableau ci-dessous présente quelques exemples de formes/figures ayant plus d’une ligne de symétrie.
 |
 |
 |
 |
 |
 |
 |
.
 Image8 Image8 |
 |
 |
 |
 |
 |
 |
 |
Exemples réels de symétrie
.exemples de symétrie dans la vie réelle
-
Réflexion d’arbres dans une eau claire et réflexion de montagnes dans un lac.
-
Les ailes de la plupart des papillons sont identiques sur les côtés gauche et droit.
-
Certains visages humains sont identiques sur les côtés gauche et droit.
-
Les gens peuvent aussi avoir une moustache symétrique.

Exemple 3 : Lequel des éléments suivants n’est pas une ligne de symétrie ?
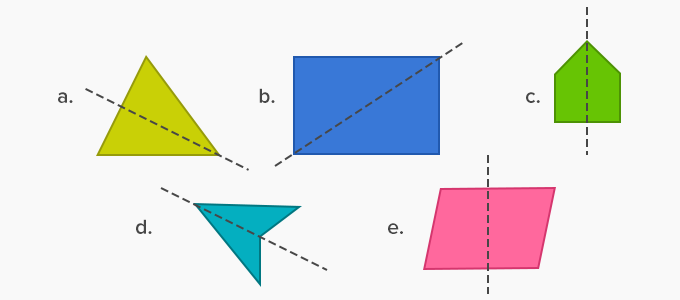
Réponse : (b) et (e) n’a pas de ligne de symétrie.
Exemple 4 : Sont donnés ci-dessous la partie gauche d’un tableau et sa ligne de symétrie. Complétez le tableau.

Solution:
Le tableau complet est celui indiqué ci-dessous.

.