Sudoku GeneratorSudoku SolverDaily Sudoku
Killer Sudoku GeneratorKiller Sudoku Solver
Super Sudoku GeneratorSuper Sudoku Solver
Samurai GeneratorSamurai SolverGodoku SolverHomeNewsHow To Play SudokuSign Up !Profil du membreConcoursLe programme SudokuFoire aux questions sur le SudokuNewsletterLivres SudokuLiens SudokuSyndicationContact Us
Comme vu sur Times Online en février 2007
En novembre 2006, The Times a introduit un nouveau niveau extrême de Sudoku donnant aux joueurs un niveau de logique plus difficile : Super Fiendish. Beaucoup ont accueilli ce nouveau défi, mais certains ont demandé de l’aide. Ainsi, alors que nous augmentons la difficulté Super Fiendish, le moment est venu de présenter les techniques essentielles pour résoudre les énigmes Sudoku les plus difficiles.
Veuillez être rassuré : toutes les énigmes Sudoku publiées dans le Times sont toujours solubles par des moyens logiques. Nous vous présentons ici les techniques qui vous aideront à résoudre les énigmes les plus difficiles en utilisant uniquement la logique et sans deviner.
D’abord quelques points préliminaires : si vous avez déjà complété un Sudoku Fiendish ou Super Fiendish, vous serez familier avec le fait de noter les candidats ou les marques de crayon. Les marques de crayon sont de petits nombres, généralement écrits en haut de chaque case non résolue, énumérant toutes les valeurs possibles pour cette case. Dans de nombreuses techniques avancées, la clé est de repérer des modèles dans vos marques de crayon pour éliminer les possibilités dans d’autres carrés. Chaque fois que vous résolvez une case, vous devez supprimer ce nombre des marques de crayon dans toutes les autres cases de la même ligne, de la même colonne et du même bloc.
La technique de l’aile x
Essentiellement, cette méthode utilise le fait que dans certains cas, il n’y a que deux façons possibles de placer deux nombres dans quatre cases qui forment un rectangle. Il existe une relation entre les carrés diagonalement opposés, d’où le « x » de x-wing. Le terme x-wing dérive lui-même des chasseurs x-wing dans Star Wars.
Le Sudoku de la figure 1 est partiellement résolu en utilisant des techniques de résolution de difficulté facile et moyenne : singles, singles cachés et intersections de colonnes/blocs. Maintenant, plus aucune case ne peut être résolue avec ces techniques ; vous êtes coincé. Dans le diagramme, il y a des marques de crayon complètes pour tous les carrés des rangées trois et sept, et une intersection colonne/bloc nécessaire pour éliminer une marque de crayon 7.
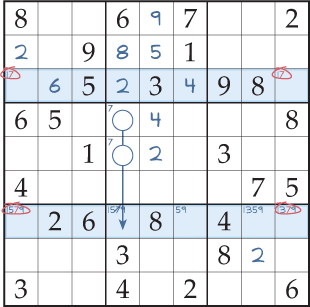Figure 1
Considérez où vous pourriez placer le 7 sur les troisième et septième rangées (en surbrillance). Vous savez qu’il doit être placé une fois, et une seule, sur chacune de ces rangées. Ici, les seules cases où le 7 est possible se trouvent dans la première et la dernière colonne. C’est un fait que vous ne pouvez pas placer le 7 dans la case de la première colonne des deux rangées surlignées en même temps. Vous ne pouvez pas non plus les placer toutes les deux dans la dernière colonne. Par conséquent, ils doivent être placés dans des coins diagonalement opposés : un 7 dans la première colonne ; un 7 dans la dernière.
Donc, il y a deux façons possibles de placer le 7 ; en quoi cela vous aide-t-il à résoudre quoi que ce soit ? Eh bien, vous avez établi que le 7 de la première colonne doit se trouver dans l’une des deux rangées surlignées ; pas dans d’autres cases de cette colonne. Vous pouvez maintenant rayer la marque de crayon 7 de toutes les autres cases de la première colonne. En utilisant la même logique dans la dernière colonne, vous pouvez également éliminer le 7 de toutes les cases qui ne se trouvent pas dans l’une des deux lignes surlignées (Fig. 2). Cela laisse une case dans la première colonne avec seulement une marque de crayon, donc vous pouvez maintenant placer le 9. Maintenant que cette case est résolue, vous pouvez compléter le Sudoku en utilisant des méthodes faciles.
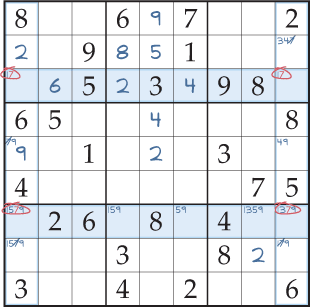Figure 2
En général, une aile x est trouvée lorsque pour deux rangées, il y a deux, et seulement deux, cases possibles dans lesquelles un nombre particulier peut être placé, et pour les deux rangées, ces cases se trouvent dans les deux mêmes colonnes. Dans ce cas, ce nombre particulier peut être éliminé comme possibilité pour toutes les autres cases de ces deux colonnes. Bien sûr, vous pouvez échanger les rangées et les colonnes dans cette définition.
La technique de l’Espadon
C’est une méthode plus difficile, l’une des plus compliquées pour tout Sudoku que vous trouverez en version imprimée. À partir d’aujourd’hui, vous constaterez que la technique de l’espadon est devenue un sujet régulier dans le Times2 . L’espadon est similaire à la technique de l’aile x, mais à une échelle plus grande, avec trois lignes et colonnes au lieu de deux. La technique de l’espadon doit son nom à un biplan de la Seconde Guerre mondiale appelé « Fairey Swordfish », un biplan de reconnaissance et de repérage des torpilles utilisé par la Royal Navy de 1936 à 1945. Si l’on trace des lignes le long des lignes et des colonnes, reliant les carrés concernés, ils peuvent former deux rectangles, reliés aux angles. Cela ressemble aux ailes d’un biplan, séparées par des entretoises.
On trouve un espadon lorsque pour trois lignes, il y a deux ou trois carrés possibles dans lesquels un nombre particulier peut être placé, et que pour les trois lignes, ces carrés se trouvent dans les trois mêmes colonnes. Dans ce cas, ce nombre particulier peut être éliminé comme possibilité pour toutes les autres cases de ces trois colonnes. Bien sûr, vous pouvez échanger les rangées et les colonnes dans cette définition.
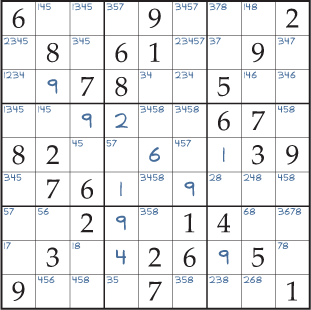Figure 3
La figure 3 est un Sudoku partiellement résolu, en utilisant des techniques de résolution de difficulté facile et moyenne ; aucun autre carré ne peut être résolu en les utilisant. Pour vous donner une bonne chance de repérer l’espadon, vous devez entrer toutes les marques de crayon dans la grille comme indiqué ici.
Il n’y a pas de voies faciles pour repérer le motif de l’espadon. Essayez donc de vous concentrer sur un seul chiffre de 1 à 9 à tour de rôle lorsque vous balayez vos marques de crayon en lignes et en colonnes. Regardez le long de chacune des lignes à tour de rôle, en notant chacune d’entre elles qui ne contient que deux ou trois cases avec le nombre actuel comme possibilité. Ensuite, regardez s’il existe trois rangées où les carrés tombent tous dans trois colonnes. Si vous ne trouvez rien, essayez à nouveau avec les colonnes à la place des rangées.
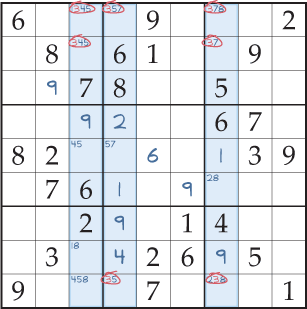Figure 4
Dans la figure 4, les marques de crayon pertinentes sont inscrites pour montrer que vous avez deux carrés possibles dans lesquels le 3 peut être placé dans les troisième et quatrième colonnes, et trois carrés possibles dans la septième colonne (en surbrillance). Il est important de noter que tous ces carrés possibles ne se trouvent que sur trois rangées. Par conséquent, sur chacune des trois rangées qui se croisent, le 3 doit être placé dans l’une des colonnes mises en évidence. Ainsi, vous pouvez éliminer la marque de crayon 3 de tous les autres carrés non résolus dans ces rangées qui se croisent (Fig. 5). Ces éliminations, en plus d’une intersection colonne/bloc pour éliminer une marque de crayon 7, ne laissent qu’une marque de crayon dans la dernière case de la deuxième rangée, de sorte que vous pouvez maintenant la résoudre pour être un 4.
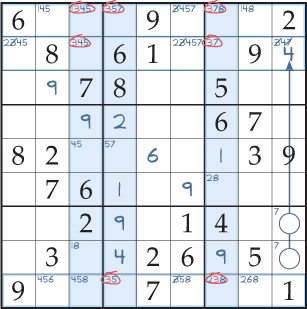Figure 5
Si vous aimez jouer à des Sudokus sérieusement difficiles, essayez les énigmes à la fin du livre The Times Sudoku 6 avec certaines nécessitant la technique de l’espadon. Si vous aimez vraiment Super Fiendish, vous devrez attendre un peu plus longtemps pour The Times Sudoku 7 avec 25 Sudokus extrêmement durs, dont beaucoup nécessitent le x-wing ou l’swordfish pour les compléter.
Générez un nouveau Sudoku
.