Contenu :
- Qu’est-ce qu’un test T ?
- Le score T
- Valeurs T et valeurs P
- Calcul du test T
- Qu’est-ce qu’un test T apparié (test T à échantillons appariés) ?
Qu’est-ce qu’un test T ?
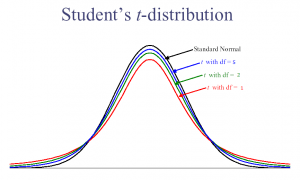
Divers degrés de liberté pour le T de Student.
Le test t vous indique dans quelle mesure les différences entre les groupes sont significatives ; en d’autres termes, il vous permet de savoir si ces différences (mesurées en moyennes) ont pu se produire par hasard.
Un exemple très simple : Disons que vous avez un rhume et que vous essayez un remède naturopathique. Votre rhume dure quelques jours. La fois suivante, vous achetez un produit pharmaceutique en vente libre et le rhume dure une semaine. Vous interrogez vos amis et ils vous disent tous que leur rhume a duré moins longtemps (en moyenne 3 jours) lorsqu’ils ont pris le remède homéopathique. Ce que vous voulez vraiment savoir, c’est si ces résultats sont reproductibles. Un test t peut vous le dire en comparant les moyennes des deux groupes et en vous permettant de connaître la probabilité que ces résultats se produisent par hasard.
Un autre exemple : Les tests T de Student peuvent être utilisés dans la vie réelle pour comparer des moyennes. Par exemple, une société pharmaceutique peut vouloir tester un nouveau médicament contre le cancer pour savoir s’il améliore l’espérance de vie. Dans une expérience, il y a toujours un groupe de contrôle (un groupe qui reçoit un placebo, ou « pilule de sucre »). Le groupe témoin peut avoir une espérance de vie moyenne de +5 ans, tandis que le groupe qui prend le nouveau médicament peut avoir une espérance de vie de +6 ans. Il semblerait que le médicament soit efficace. Mais cela pourrait être dû à un coup de chance. Pour le vérifier, les chercheurs utiliseraient un test t de Student afin de savoir si les résultats sont reproductibles pour une population entière.
Vous avez toujours des difficultés ? Chegg.com vous mettra en relation avec un tuteur virtuel (et vos 30 premières minutes sont gratuites !).
Le score T.
Le score t est un rapport entre la différence entre deux groupes et la différence au sein des groupes. Plus le score t est grand, plus il y a de différence entre les groupes. Plus le score t est petit, plus il y a de similitude entre les groupes. Un score t de 3 signifie que les groupes sont trois fois plus différents les uns des autres qu’ils ne le sont au sein d’un même groupe. Lorsque vous effectuez un test t, plus la valeur t est grande, plus il est probable que les résultats soient reproductibles.
- Un grand score t vous indique que les groupes sont différents.
- Un petit score t vous indique que les groupes sont similaires.
Valeurs t et valeurs p
Combien est » assez grand » ? Chaque valeur t a une valeur p qui l’accompagne. Une valeur p est la probabilité que les résultats de votre échantillon de données se soient produits par hasard. Les valeurs P vont de 0 à 100 %. Elles s’écrivent généralement sous la forme d’une décimale. Par exemple, une valeur p de 5 % est de 0,05. Les valeurs p faibles sont bonnes ; elles indiquent que vos données ne sont pas le fruit du hasard. Par exemple, une valeur p de 0,01 signifie qu’il y a seulement 1 % de probabilité que les résultats d’une expérience soient le fruit du hasard. Dans la plupart des cas, une valeur p de 0,05 (5 %) est acceptée pour signifier que les données sont valides.
Calcul de la statistique / Types de tests
Il existe trois principaux types de tests t :
- Un test t pour échantillons indépendants compare les moyennes de deux groupes.
- Un test t à échantillons appariés compare les moyennes d’un même groupe à des moments différents (disons, à un an d’intervalle).
- Un test t à un échantillon teste la moyenne d’un seul groupe par rapport à une moyenne connue.
Vous ne voulez probablement pas calculer le test à la main (les mathématiques peuvent devenir très désordonnées, mais si vous insistez, vous pouvez trouver les étapes pour un test t à échantillons indépendants ici.
Utilisez les outils suivants pour calculer le test t :
Comment faire un test T dans Excel.
Test T dans SPSS.
Distribution T sur la TI 89.
Distribution T sur la TI 83.
Qu’est-ce qu’un test T apparié (test T sur échantillons appariés / test T sur échantillons dépendants) ?
Un test T apparié (également appelé test T sur paires corrélées, test T sur échantillons appariés ou test T sur échantillons dépendants) consiste à effectuer un test T sur des échantillons dépendants. Les échantillons dépendants sont essentiellement connectés – ce sont des tests sur la même personne ou la même chose. Par exemple :
- Frais d’IRM du genou dans deux hôpitaux différents,
- Deux tests sur la même personne avant et après la formation,
- Deux mesures de la pression artérielle sur la même personne en utilisant des équipements différents.
Quand choisir un test T apparié / test T à échantillons appariés / test T à échantillons dépendants
Choisissez le test t apparié si vous avez deux mesures sur le même élément, la même personne ou la même chose. Vous devriez également choisir ce test si vous avez deux éléments qui sont mesurés avec une condition unique. Par exemple, vous pouvez mesurer les performances de sécurité des voitures dans le cadre du programme Vehicle Research and Testing et soumettre les voitures à une série de crash tests. Bien que les constructeurs soient différents, vous pourriez les soumettre aux mêmes conditions.
Avec un test t « régulier » à deux échantillons, vous comparez les moyennes de deux échantillons différents. Par exemple, vous pourriez tester deux groupes différents d’associés du service client sur un test lié aux affaires ou tester des étudiants de deux universités sur leurs compétences en anglais. Si vous prenez un échantillon aléatoire de chaque groupe séparément et qu’ils ont des conditions différentes, vos échantillons sont indépendants et vous devez exécuter un test t d’échantillons indépendants (également appelé entre échantillons et échantillons non appariés).
L’hypothèse nulle pour le test t d’échantillons indépendants est μ1 = μ2. En d’autres termes, elle suppose que les moyennes sont égales. Avec le test t apparié, l’hypothèse nulle est que la différence par paire entre les deux tests est égale (H0 : µd = 0). La différence entre les deux tests est très subtile ; celui que vous choisissez repose sur votre méthode de collecte de données.
Test T d’échantillons appariés à la main
Exemple de question : Calculez un test t apparié à la main pour les données suivantes :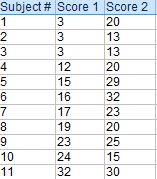
Étape 1 : soustrayez chaque score Y de chaque score X.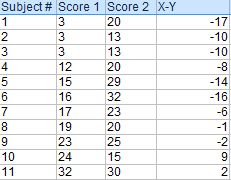
Étape 2 : additionnez toutes les valeurs de l’étape 1.
Mettez ce nombre de côté pour un moment.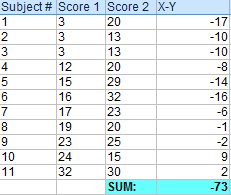
Étape 3 : Élevez au carré les différences de l’étape 1.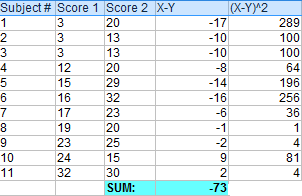
Étape 4 : Additionnez toutes les différences élevées au carré de l’étape 3.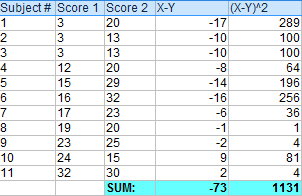
Étape 5 : Utilisez la formule suivante pour calculer le score t :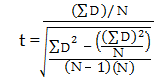
- ΣD : Somme des différences (Somme des X-Y de l’étape 2)
- ΣD2 : Somme des différences au carré (de l’étape 4)
- (ΣD)2 : Somme des différences (de l’étape 2), au carré.
Si vous n’êtes pas familier avec Σ, vous pouvez d’abord lire la notation de la somme.
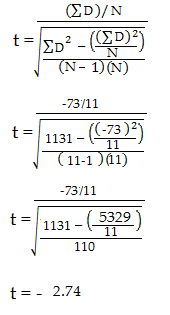
Étape 6 : soustrayez 1 de la taille de l’échantillon pour obtenir les degrés de liberté. Nous avons 11 items, donc 11-1 = 10.
Étape 7 : Trouvez la valeur p dans le tableau t, en utilisant les degrés de liberté de l’étape 6. Si vous n’avez pas de niveau alpha spécifié, utilisez 0,05 (5 %). Pour cet exemple de problème, avec df = 10, la valeur t est de 2,228.
Étape 8 : Comparez la valeur de votre tableau t de l’étape 7 (2,228) à votre valeur t calculée (-2,74). La valeur t calculée est supérieure à la valeur du tableau à un niveau alpha de 0,05. La valeur p est inférieure au niveau alpha : p <.05. Nous pouvons rejeter l’hypothèse nulle selon laquelle il n’y a pas de différence entre les moyennes.
Note : Vous pouvez ignorer le signe moins lorsque vous comparez les deux valeurs t, car &pm ; indique le sens ; la valeur p reste la même pour les deux sens.
Voyez notre chaîne YouTube pour plus d’aide et de conseils sur les statistiques !
Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York : Wiley, p. 50-55, 1956.
Stephanie Glen. » Test T (test T de Student) : Définition et exemples » de StatisticsHowTo.com : Des statistiques élémentaires pour le reste d’entre nous ! https://www.statisticshowto.com/probability-and-statistics/t-test/
——————————————————————————
Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert en la matière. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !