Mécanique des matériaux
Équations de contraintes de cisaillement et applications
Contrainte de cisaillement générale :
La formule pour calculer la contrainte de cisaillement moyenne est :
où τ = la contrainte de cisaillement ; F = la force appliquée ; A = la section transversale du matériau dont la surface est perpendiculaire au vecteur de force appliqué ;
Cisaillement de poutre :
Le cisaillement de poutre est défini comme la contrainte de cisaillement interne d’une poutre causée par la force de cisaillement appliquée à la poutre.
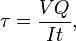où V = force de cisaillement totale à l’endroit en question ; Q = moment statique de l’aire ; t = épaisseur dans le matériau perpendiculaire au cisaillement ; I = moment d’inertie de l’ensemble de la section transversale. Cette formule est également connue sous le nom de formule de Jourawski.Cisaillement semi-monocoqueLes contraintes de cisaillement dans une structure semi-monocoque peuvent être calculées en idéalisant la section transversale de la structure en un ensemble de longerons (supportant uniquement des charges axiales) et d’âmes (supportant uniquement des flux de cisaillement). En divisant le flux de cisaillement par l’épaisseur d’une partie donnée de la structure semi-monocoque, on obtient la contrainte de cisaillement. Ainsi, la contrainte de cisaillement maximale se produira soit dans l’âme du flux de cisaillement maximal, soit dans celle de l’épaisseur minimale.Les constructions dans le sol peuvent également céder sous l’effet du cisaillement, par exemple, Le poids d’un barrage ou d’une digue remplie de terre peut provoquer l’effondrement du sous-sol, comme un petit glissement de terrain.Cisaillement par impactLa contrainte de cisaillement maximale créée dans une barre ronde pleine soumise à un impact est donnée par l’équation :
où U = variation de l’énergie cinétique ; G = module de cisaillement ; V = volume de la barre ; et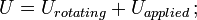 
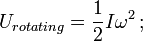
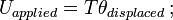
= moment d’inertie de la masse ; ω = vitesse angulaire.
Contrainte de cisaillement dans les fluides :
Tout fluide réel (liquides et gaz inclus) se déplaçant le long d’une frontière solide subira une contrainte de cisaillement sur cette frontière. La condition de non-glissement impose que la vitesse du fluide à la frontière (par rapport à la frontière) soit nulle, mais à une certaine hauteur de la frontière, la vitesse d’écoulement doit être égale à celle du fluide. La région située entre ces deux points est appelée à juste titre la couche limite. Pour tous les fluides newtoniens en écoulement laminaire, la contrainte de cisaillement est proportionnelle à la vitesse de déformation du fluide, la viscosité étant la constante de proportionnalité. Cependant, pour les fluides non newtoniens, ce n’est plus le cas car la viscosité n’est pas constante. La contrainte de cisaillement est appliquée à la frontière en raison de cette perte de vitesse. La contrainte de cisaillement, pour un fluide newtonien, au niveau d’un élément de surface parallèle à une plaque plane, au point y, est donnée par :
où μ est la viscosité dynamique du fluide ; u est la vitesse du fluide le long de la frontière ; y est la hauteur au-dessus de la frontière. Plus précisément, la contrainte de cisaillement de paroi est définie comme suit :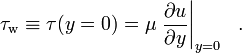 
En cas de vent, la contrainte de cisaillement à la frontière est appelée contrainte de vent.
1. Timoshenko, Stephen P. (1983), History of Strength of Material, Courier Dover Publications, p. 141, ISBN 0486611876, http://books.google.com/?id=tkScQmyhsb8C .
2. Day, Michael A. (2004), The no-slip condition of fluid dynamics, Springer Netherlands, p. 285-296, ISSN (Print) 1572-8420 (Online) 0165-0106 (Print) 1572-8420 (Online), http://www.springerlink.com/content/k1m4t1p02m778u88/.
3. Naqwi, A. A.; Reynolds, W. C. (jan 1987), « Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow », NASA STI/Recon Technical Report N 87
4. Große, S. ; Schröder, W. (2009), « Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars », AIAA Journal 47 (2) : 314-321, Bibcode 2009AIAAJ..47..314G, doi:10.2514/1.36892
5. Große, S. ; Schröder, W. (2008), « Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³ », International Journal of Heat and Fluid Flow 29 (3) : 830-840, doi:10.1016/j.ijheatfluidflow.2008.01.008
.