Lernziele
Am Ende dieses Abschnitts können Sie:
- Erläutern Sie, wie Zeitintervalle in verschiedenen Bezugsrahmen unterschiedlich gemessen werden können.
- Beschreiben Sie, wie man ein richtiges Zeitintervall von einem gedehnten Zeitintervall unterscheidet.
- Beschreiben Sie die Bedeutung des Myonen-Experiments.
- Erläutern Sie, warum das Zwillingsparadoxon kein Widerspruch ist.
- Berechnen Sie die Zeitdilatation bei gegebener Geschwindigkeit eines Objekts in einem gegebenen Bezugssystem.
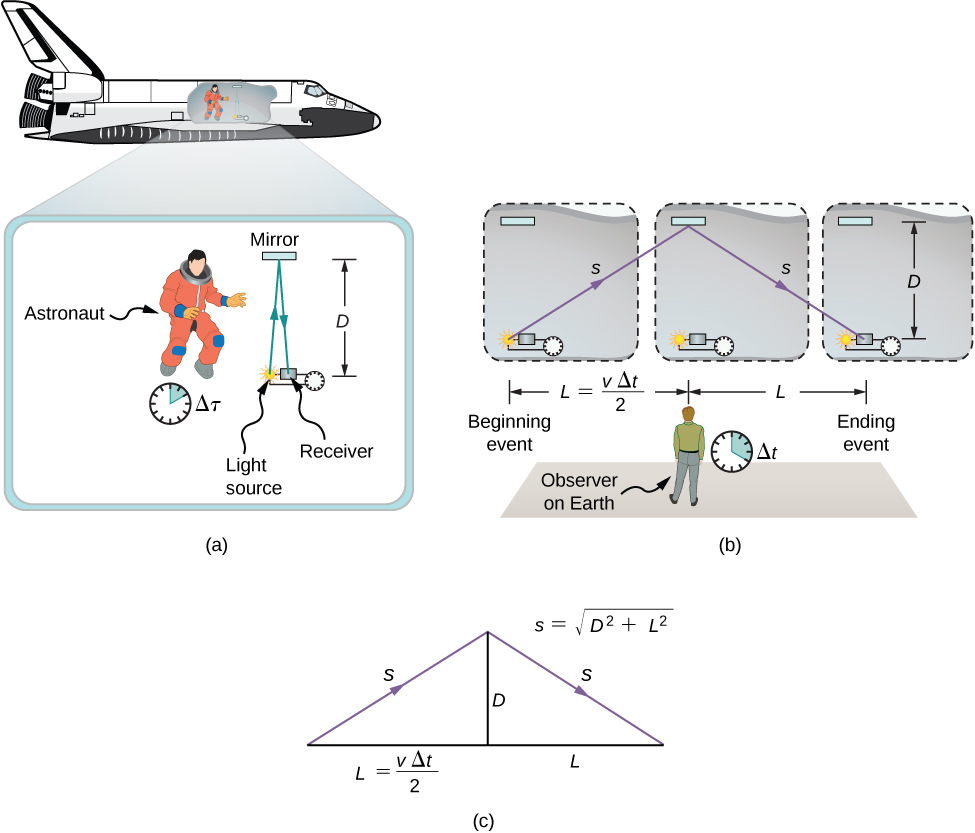
Die Analyse der Gleichzeitigkeit zeigt, dass die Einsteinschen Postulate einen wichtigen Effekt implizieren: Zeitintervalle haben unterschiedliche Werte, wenn sie in verschiedenen Inertialsystemen gemessen werden. Nehmen wir zum Beispiel an, ein Astronaut misst die Zeit, die ein Lichtimpuls benötigt, um eine Strecke senkrecht zur Bewegungsrichtung seines Schiffes (relativ zu einem erdgebundenen Beobachter) zurückzulegen, an einem Spiegel abzuprallen und zurückzukehren (Abbildung \(\PageIndex{1a}\)). Wie verhält sich die verstrichene Zeit, die der Astronaut im Raumschiff misst, zu der verstrichenen Zeit, die ein erdgebundener Beobachter durch Beobachtung des Geschehens im Raumschiff misst?
Die Untersuchung dieser Frage führt zu einem tiefgreifenden Ergebnis. Die verstrichene Zeit für einen Vorgang hängt davon ab, welcher Beobachter ihn misst. In diesem Fall ist die vom Astronauten gemessene Zeit (innerhalb des Raumschiffs, in dem der Astronaut ruht) kleiner als die vom erdgebundenen Beobachter gemessene Zeit (zu dem sich der Astronaut bewegt). Die Zeit, die für den gleichen Vorgang vergeht, ist für die Beobachter unterschiedlich, weil die Strecke, die der Lichtimpuls im Körper des Astronauten zurücklegt, kleiner ist als im Körper des erdgebundenen Beobachters, wie in Abbildung \(\PageIndex{1b}\) zu sehen. Das Licht bewegt sich in jedem Rahmen mit der gleichen Geschwindigkeit, so dass es mehr Zeit benötigt, um die größere Entfernung im erdgebundenen Rahmen zurückzulegen.
Definition: Zeitdilatation
Die Zeitdilatation ist die Verlängerung des Zeitintervalls zwischen zwei Ereignissen für einen Beobachter in einem Inertialsystem, das sich in Bezug auf das Ruhegitter der Ereignisse bewegt (in dem die Ereignisse am gleichen Ort stattfinden).
Um die Zeitmessungen in den beiden Inertialrahmen quantitativ zu vergleichen, können wir die Entfernungen in Abbildung \(\PageIndex{1b}\) zueinander in Beziehung setzen und dann jede Entfernung in Form der Laufzeit (bzw. entweder \(\Delta t\) oder \(\Delta \tau\)) des Impulses im entsprechenden Bezugsrahmen ausdrücken. Die resultierende Gleichung kann dann für \(\Delta t\) in Bezug auf \(\Delta \tau\) gelöst werden.
Die Längen \(D\) und \(L\) in Abbildung \(\PageIndex{1c}\) sind die Seiten eines rechtwinkligen Dreiecks mit Hypotenuse \(s\). Aus dem Satz des Pythagoras,
Die Längen \(2s\) und \(2L\) sind jeweils die Entfernungen, die der Lichtimpuls und das Raumschiff in der Zeit \(\Delta t\) im Rahmen des erdgebundenen Beobachters zurücklegen. Die Länge \(D\) ist die Entfernung, die der Lichtpuls in der Zeit \(\Delta t\) im Rahmen des Astronauten zurücklegt. Daraus ergeben sich drei Gleichungen:
2L &= v\Delta t; \\\ 2D &= c\Delta \tau. \end{align*}\]
Beachten Sie, dass wir Einsteins zweites Postulat verwendet haben, indem wir die Lichtgeschwindigkeit in beiden Inertialsystemen mit c annahmen. Wir ersetzen diese Ergebnisse in den vorherigen Ausdruck aus dem Satz des Pythagoras:
\left(c\dfrac{\Delta t}{2}\right)^2 &= \left(c\dfrac{\Delta \tau}{2}\right)^2 + \left(v\dfrac{\Delta t}{2}\right)^2 \end{align*}\]
Dann ordnen wir um und erhalten
Schließlich, Die Lösung von \(\Delta t\) in Bezug auf \(\Delta \tau\) ergibt
Dies ist äquivalent zu
wobei \(\gamma\) der relativistische Faktor (oft Lorentz-Faktor genannt), gegeben durch
und \(v\) und \(c\) sind die Geschwindigkeiten des bewegten Beobachters und des Lichts, beziehungsweise.
Beachten Sie die Asymmetrie zwischen den beiden Messungen. Nur eine von ihnen ist eine Messung des Zeitintervalls zwischen zwei Ereignissen – dem Aussenden und dem Eintreffen des Lichtimpulses – an der gleichen Position. Es ist eine Messung des Zeitintervalls im Ruhezustand einer einzelnen Uhr. Bei der Messung im erdgebundenen Rahmen wird der Zeitabstand zwischen zwei Ereignissen verglichen, die an unterschiedlichen Orten auftreten. Das Zeitintervall zwischen Ereignissen, die an einem einzigen Ort stattfinden, hat einen eigenen Namen, um es von der vom erdgebundenen Beobachter gemessenen Zeit zu unterscheiden, und wir verwenden das separate Symbol \(\Delta \tau\), um uns in diesem Kapitel darauf zu beziehen.
Definition: Proper Time
Das Eigenzeitintervall \(\Delta \tau\) zwischen zwei Ereignissen ist das Zeitintervall, das von einem Beobachter gemessen wird, für den beide Ereignisse am selben Ort stattfinden.
Die Gleichung, die \(\delta t\) und \(\Delta \tau\) in Beziehung setzt, ist wirklich bemerkenswert. Erstens ist, wie bereits erwähnt, die verstrichene Zeit für verschiedene Beobachter, die sich relativ zueinander bewegen, nicht dieselbe, auch wenn sich beide in Inertialrahmen befinden. Ein eigenes Zeitintervall \(\Delta \tau\) für einen Beobachter, der sich, wie der Astronaut, mit dem Gerät bewegt, ist kleiner als das Zeitintervall für andere Beobachter. Es ist die kleinstmögliche gemessene Zeit zwischen zwei Ereignissen. Der erdgebundene Beobachter sieht Zeitintervalle innerhalb des bewegten Systems als gedehnt (d.h. verlängert) im Vergleich dazu, wie der sich relativ zur Erde bewegende Beobachter sie innerhalb des bewegten Systems sieht. Alternativ vergeht nach Ansicht des erdgebundenen Beobachters weniger Zeit zwischen Ereignissen innerhalb des bewegten Systems. Beachten Sie, dass die kürzeste Zeit zwischen den Ereignissen in dem Inertialsystem vergeht, in dem der Beobachter die Ereignisse (z. B. die Aussendung und Ankunft des Lichtsignals) am gleichen Punkt sieht.
Dieser Zeiteffekt ist real und wird nicht durch ungenaue Uhren oder falsche Messungen verursacht. Die Zeitmessungen desselben Ereignisses unterscheiden sich für Beobachter in relativer Bewegung. Die Zeitdilatation ist eine intrinsische Eigenschaft der Zeit selbst. Alle Uhren, die sich relativ zu einem Beobachter bewegen, einschließlich biologischer Uhren, wie z. B. der Herzschlag eines Menschen, oder das Altern, laufen langsamer im Vergleich zu einer Uhr, die relativ zum Beobachter stationär ist.
Beachten Sie, dass, wenn die relative Geschwindigkeit viel kleiner als die Lichtgeschwindigkeit (v << c) ist, dann ist \(v^2/c^2\) extrem klein, und die verstrichenen Zeiten \(\Delta t\) und \(\Delta \tau\) sind fast gleich. Bei kleinen Geschwindigkeiten nähert sich die auf der modernen Relativitätstheorie basierende Physik der klassischen Physik an – alltägliche Erfahrungen beinhalten sehr kleine relativistische Effekte. Für Geschwindigkeiten nahe der Lichtgeschwindigkeit ist \(v^2/c^2\) jedoch nahe bei eins, so dass \(\sqrt{1 – v^2/c^2}\) sehr klein ist und \(\Delta t\) deutlich größer wird als \(\Delta \tau\).
Halbwertszeit eines Myons
Es gibt zahlreiche experimentelle Beweise dafür, dass die Gleichung \(\Delta t = \gamma \Delta \tau\) korrekt ist. Ein Beispiel dafür sind die Teilchen der kosmischen Strahlung, die kontinuierlich aus dem tiefen Weltraum auf die Erde niederregnen. Einige Kollisionen dieser Teilchen mit Kernen in der oberen Atmosphäre führen zu kurzlebigen Teilchen, die Myonen genannt werden. Die Halbwertszeit (Zeitspanne, in der die Hälfte eines Materials zerfällt) eines Myons beträgt 1,52 μs, wenn es sich relativ zum Beobachter, der die Halbwertszeit misst, in Ruhe befindet. Dies ist das richtige Zeitintervall \(\Delta \tau\). Diese kurze Zeit erlaubt es nur sehr wenigen Myonen, die Erdoberfläche zu erreichen und entdeckt zu werden, wenn die Newtonschen Annahmen über Zeit und Raum korrekt wären. Die von den Teilchen der kosmischen Strahlung erzeugten Myonen haben jedoch eine Reihe von Geschwindigkeiten, von denen sich einige nahe der Lichtgeschwindigkeit bewegen. Es wurde festgestellt, dass die Halbwertszeit des Myons, wie sie von einem erdgebundenen Beobachter gemessen wird (\(\Delta t\)), mit der Geschwindigkeit variiert, genau wie es die Gleichung \(\Delta t = \gamma \Delta \tau\) vorhersagt. Je schneller sich das Myon bewegt, desto länger lebt es. Wir auf der Erde sehen, dass das Myon viel länger lebt, als seine Halbwertszeit in seinem eigenen Ruhesystem vorhersagt. Aus unserem Blickwinkel betrachtet, zerfällt das Myon langsamer als in seinem Ruhezustand relativ zu uns. Ein weitaus größerer Teil der Myonen erreicht daher den Boden.
Bevor wir das erste Beispiel für die Lösung eines Problems in der Relativitätstheorie vorstellen, geben wir eine Strategie an, die Sie als Leitfaden für diese Berechnungen verwenden können.
PROBLEMLÖSUNGSSTRATEGIE: RELATIVITÄT
- Machen Sie eine Liste dessen, was gegeben ist oder aus der Problemstellung gefolgert werden kann (identifizieren Sie die bekannten Punkte). Suchen Sie insbesondere nach Informationen über die Relativgeschwindigkeit v.
- Identifizieren Sie genau, was in der Aufgabe bestimmt werden muss (identifizieren Sie die Unbekannten).
- Vergewissern Sie sich, dass Sie die konzeptionellen Aspekte der Aufgabe verstehen, bevor Sie Berechnungen durchführen (drücken Sie die Antwort als Gleichung aus). Entscheiden Sie z. B., welcher Beobachter die Zeitdilatation oder die Längenkontraktion sieht, bevor Sie mit den Gleichungen arbeiten oder sie zur Berechnung verwenden. Wenn Sie sich Gedanken darüber gemacht haben, wer was sieht, wer sich mit dem beobachteten Ereignis bewegt, wer die Eigenzeit sieht usw., wird es Ihnen viel leichter fallen, festzustellen, ob Ihre Berechnung sinnvoll ist.
- Bestimmen Sie die primäre Art der Berechnung, die durchgeführt werden muss, um die oben identifizierten Unbekannten zu finden (führen Sie die Berechnung durch). Die Zusammenfassung des Abschnitts ist hilfreich, um festzustellen, ob es sich um eine Längenkontraktion, relativistische kinetische Energie oder ein anderes Konzept handelt.
Beachten Sie, dass Sie bei der Berechnung nicht abrunden sollten. Wie im Text erwähnt, müssen Sie Ihre Berechnungen oft auf viele Stellen ausführen, um den gewünschten Effekt zu sehen. Sie können ganz am Ende der Problemlösung abrunden, aber verwenden Sie eine gerundete Zahl nicht in einer nachfolgenden Berechnung. Überprüfen Sie außerdem die Antwort, um zu sehen, ob sie sinnvoll ist: Ergibt sie einen Sinn? Dies kann bei der Relativitätstheorie schwieriger sein, da es nur wenige Beispiele aus dem Alltag gibt, an denen man sehen kann, was sinnvoll ist. Aber Sie können nach Geschwindigkeiten größer als c oder nach relativistischen Effekten suchen, die in die falsche Richtung gehen (wie eine Zeitkontraktion, wo eine Dilatation erwartet wurde).
Beispiel \(\PageIndex{1A}\): Zeitdilatation in einem Hochgeschwindigkeitsfahrzeug
Das Hypersonic Technology Vehicle 2 (HTV-2) ist ein experimentelles Raketenfahrzeug, das sich mit 21.000 km/h (5830 m/s) fortbewegen kann. Wenn eine elektronische Uhr im HTV-2 ein Zeitintervall von genau 1 s Dauer misst, wie groß wäre dann das Zeitintervall für Beobachter auf der Erde?
Strategie
Wenden Sie die Zeitdilatationsformel an, um das richtige Zeitintervall des Signals im HTV-2 mit dem auf der Erde gemessenen Zeitintervall in Beziehung zu setzen.
Lösung
- Identifizieren Sie die Bekannten: \(\Delta \tau = 1 \, s\); \(v = 5830m/s.\)
- Identifizieren Sie die Unbekannten: \(\Delta t\).
- Drücken Sie die Antwort als Gleichung aus:
\
- Berechnen Sie. Verwenden Sie den Ausdruck für \(\gamma\), um \(\Delta t\) aus \(\Delta \tau\) zu bestimmen:
&= 1,000000000189 \, s \\ &= 1 \, s + 1,89 \times 10^{-10}s. \end{align*}\]
Bedeutung
Die sehr hohe Geschwindigkeit des HTV-2 ist immer noch nur das 10-5-fache der Lichtgeschwindigkeit. Relativistische Effekte sind für das HTV-2 für fast alle Zwecke vernachlässigbar, aber nicht Null.
Welche Geschwindigkeiten sind relativistisch?
Wie schnell muss ein Fahrzeug fahren, damit sich die auf der Uhr eines Passagiers im Fahrzeug gemessene Zeit für einen Beobachter, der sie vom Boden aus misst, um 1% unterscheidet?
Strategie
Benutzen Sie die Zeitdilatationsformel, um v/c für das gegebene Zeitverhältnis zu finden.
Lösung
- Identifizieren Sie das Bekannte:
\
- Identifizieren Sie die Unbekannte: v/c.
- Drücken Sie die Antwort als Gleichung aus:
&= \dfrac{1}{\sqrt{1 – v^2/c^2}}\Delta \tau \\ \dfrac{\Delta \tau}{\Delta t} &= \sqrt{1 – v^2/c^2} \\left(\dfrac{\Delta \tau}{\Delta t}\right)^2 &= 1 – \dfrac{v^2}{c^2} \dfrac{v}{c} &= \sqrt{1 – (\Delta \tau/\Delta t)^2}. \end{align*}}]
- Berechnen Sie:
\
Bedeutung
Das Ergebnis zeigt, dass sich ein Objekt mit etwa 10% der Lichtgeschwindigkeit bewegen muss, damit seine Bewegung signifikante relativistische Zeitdilatationseffekte erzeugt.
Berechnung von \(\Delta t\) für ein relativistisches Ereignis
Angenommen, ein kosmischer Strahl kollidiert mit einem Kern in der oberen Erdatmosphäre und erzeugt ein Myon, das eine Geschwindigkeit \(v = 0,950c\) hat. Das Myon reist dann mit konstanter Geschwindigkeit und lebt 2,20 μs, gemessen im Bezugssystem des Myons. (Sie können sich dies als die interne Uhr des Myons vorstellen.) Wie lange lebt das Myon, gemessen von einem erdgebundenen Beobachter (Abbildung \(\PageIndex{2}\))?
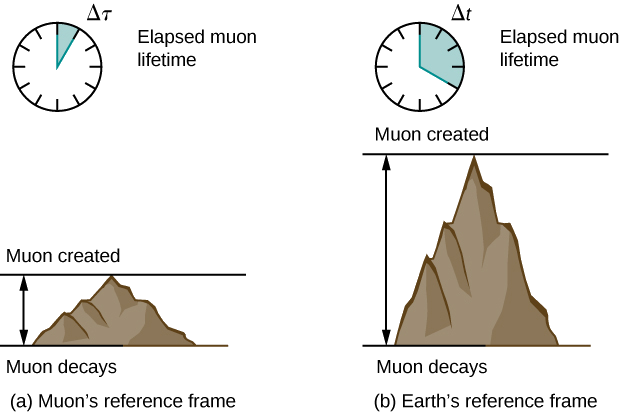
Wie wir später besprechen werden, legt das Myon im Bezugssystem der Erde eine kürzere Strecke zurück als im Bezugssystem der Erde gemessen.
Strategie
Eine Uhr, die sich mit dem Myon bewegt, misst die Eigenzeit seines Zerfallsprozesses, so dass die Zeit, die wir erhalten, \(\Delta \tau = 2,20 \mu s\) ist. Der erdgebundene Beobachter misst \(\Delta t\) wie durch die Gleichung \(\Delta t = \gamma \Delta \tau\) gegeben. Da die Geschwindigkeit gegeben ist, können wir die Zeit im Bezugssystem der Erde berechnen.
Lösung
- Identifizieren Sie die bekannten Größen: \(v = 0,950c\); \(\Delta \tau = 2,20 \mu s\).
- Identifizieren Sie die Unbekannte: \(\Delta t\).
- Drücken Sie die Antwort als Gleichung aus. Verwenden Sie:
mit
- Berechnen Sie. Verwenden Sie den Ausdruck für \(\gamma\), um \(\Delta t\) aus \(\Delta \tau\) zu bestimmen:
&=\dfrac{1}{\sqrt{1 – \dfrac{v^2}{c^2}}}\delta \tau \\\ &=\dfrac{2.20 \mu s}{\sqrt{1 – (0.950)^2}} \\ &= 7,05 \mu s.\end{align*}\]
Denken Sie daran, zusätzliche signifikante Zahlen bis zur endgültigen Antwort zu behalten.
Signifikanz
Eine Implikation dieses Beispiels ist, dass aufgrund der Tatsache, dass \(\gamma = 3,20\) bei 95,0% der Lichtgeschwindigkeit (\(v = 0,950c\)) liegt, die relativistischen Effekte signifikant sind. Die beiden Zeitintervalle unterscheiden sich um den Faktor 3,20, obwohl sie klassischerweise gleich wären. Etwas, das sich mit 0,950c bewegt, wird als hochrelativistisch bezeichnet.
Beispiel \(\PageIndex{1B}\): Relativistisches Fernsehen
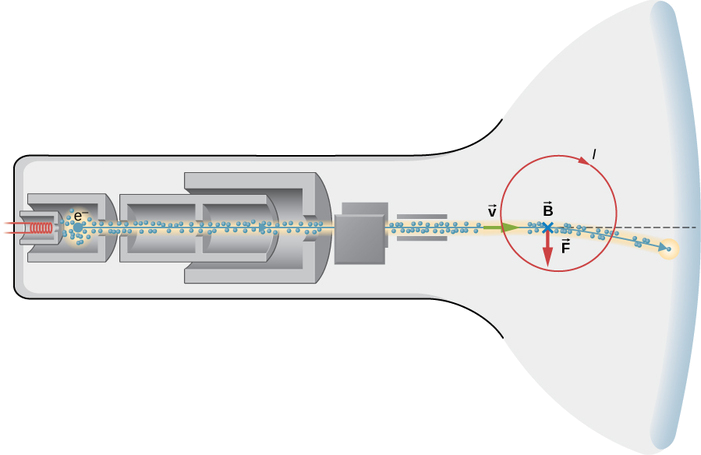
Ein Fernsehbildschirm älteren Typs ohne Flachbildschirm (Abbildung \(\PageIndex{3}\)) funktioniert, indem Elektronen über eine kurze Strecke auf relativistische Geschwindigkeit beschleunigt werden und dann elektromagnetische Felder verwendet werden, um zu steuern, wo der Elektronenstrahl auf eine fluoreszierende Schicht an der Vorderseite der Röhre trifft. Angenommen, die Elektronen bewegen sich mit \(6,00 \mal 10^7 m/s\) über eine Strecke von 0,200m0,200m vom Start des Strahls bis zum Bildschirm.
- Wie lang ist die Laufzeit eines Elektrons im Ruhezustand des Fernsehers?
- Wie lang ist die Laufzeit des Elektrons in seinem eigenen Ruhezustand?
Strategie für (a)
(a) Berechnen Sie die Zeit aus \(vt = d\). Obwohl die Geschwindigkeit relativistisch ist, erfolgt die Berechnung ausschließlich in einem Bezugssystem, so dass die Relativitätstheorie keine Rolle spielt.
Lösung
- Identifizieren Sie die bekannten Größen:
- Identifizieren Sie die Unbekannte: die Reisezeit \(\Delta t\).
- Drücken Sie die Antwort als Gleichung aus:
\
- Berechnen Sie:
&= 3,33 \Times 10^{-9} \end{align*}\]
Bedeutung
Die Reisezeit ist erwartungsgemäß extrem kurz. Da die Berechnung vollständig innerhalb eines Bezugssystems erfolgt, spielt die Relativitätstheorie keine Rolle, obwohl die Geschwindigkeit des Elektrons nahe bei c liegt.
Strategie für (b)
(b) Im Bezugssystem des Elektrons bewegt sich die Vakuumröhre und das Elektron ist stationär. Die elektronenemittierende Kathode verlässt das Elektron und die Front der Vakuumröhre trifft auf das Elektron, wobei sich das Elektron an der gleichen Stelle befindet. Daher verwenden wir die Zeitdilatationsformel, um die Eigenzeit im Elektronen-Ruhezustand auf die Zeit im Fernsehzustand zu beziehen.
Lösung
- Identifizieren Sie die bekannten Größen (aus Teil a):
\
- Identifizieren Sie die Unbekannte:
(\tau\).
- Drücken Sie die Antwort als Gleichung aus:
\
- Berechnen Sie:
&= 3,26 \times 10^{-9}s. \end{align*}\]
Bedeutung
Die Reisezeit ist im Elektronenbezugssystem kürzer. Da das Problem verlangt, für denselben Vorgang das in verschiedenen Bezugsrahmen gemessene Zeitintervall zu finden, ist die Relativitätstheorie im Spiel. Hätten wir versucht, die Zeit im Elektronen-Ruhesystem zu berechnen, indem wir einfach die 0,200 m durch die Geschwindigkeit dividiert hätten, wäre das Ergebnis wegen der relativistischen Geschwindigkeit des Elektrons leicht falsch.
Wie groß ist \(\gamma\), wenn \(v = 0.650c\)?
Antwort
Das Zwillingsparadox
Eine faszinierende Konsequenz der Zeitdilatation ist, dass ein Raumfahrer, der sich mit einer hohen Geschwindigkeit relativ zur Erde bewegt, weniger altern würde als der erdgebundene Zwilling des Astronauten. Dies ist oft als Zwillingsparadoxon bekannt. Stellen Sie sich vor, der Astronaut bewegt sich mit einer solchen Geschwindigkeit, dass \(\gamma = 30,0\), wie in Abbildung \(\PageIndex{4}\). Eine Reise, die in ihrem System 2,00 Jahre dauert, würde im System des erdgebundenen Zwillings 60,0 Jahre dauern. Angenommen, der Astronaut reist 1,00 Jahre zu einem anderen Sternensystem, erkundet kurz die Gegend und reist dann 1,00 Jahre zurück. Ein Astronaut, der zu Beginn der Reise 40 Jahre alt war, wäre bei der Rückkehr des Raumschiffs 42 Jahre alt. Alles auf der Erde hingegen wäre um 60,0 Jahre gealtert. Der erdgebundene Zwilling, wenn er noch lebt, wäre 100 Jahre alt.
Die Situation würde dem Astronauten in Abbildung \(\PageIndex{4}\) anders erscheinen. Da Bewegung relativ ist, würde das Raumschiff scheinbar stationär sein und die Erde würde sich zu bewegen scheinen. (Das ist das Gefühl, das man hat, wenn man in einem Jet fliegt.) Wenn der Astronaut aus dem Fenster des Raumschiffs schaut, würde er sehen, dass sich die Zeit auf der Erde um den Faktor \(\gamma = 30,0\) verlangsamt. Vom Raumschiff aus gesehen wird das erdgebundene Geschwisterkind nur 2/30 oder 0,07 Jahre gealtert sein, während der Astronaut 2,00 Jahre gealtert wäre.
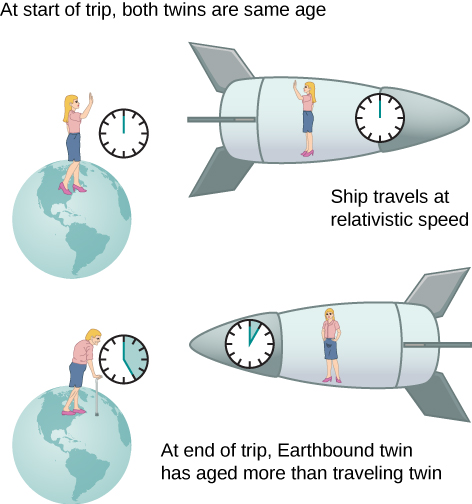
Das Paradoxon besteht hier darin, dass die beiden Zwillinge nicht beide richtig sein können. Wie bei allen Paradoxien gehen die widersprüchlichen Schlussfolgerungen von einer falschen Prämisse aus. In der Tat unterscheidet sich die Bewegung des Astronauten deutlich von der des erdgebundenen Zwillings. Die Astronautin beschleunigt auf eine hohe Geschwindigkeit und bremst dann ab, um das Sternensystem zu betrachten. Um zur Erde zurückzukehren, beschleunigt sie erneut und bremst ab. Das Raumschiff befindet sich nicht in einem einzigen Inertialsystem, auf das die Zeitdilatationsformel direkt angewendet werden kann. Das heißt, der Astronautenzwilling wechselt die Inertialreferenzen. Der erdgebundene Zwilling erfährt diese Beschleunigungen nicht und bleibt im gleichen Inertialsystem. Die Situation ist also nicht symmetrisch, und es ist falsch zu behaupten, dass der Astronaut die gleichen Effekte beobachtet wie sein Zwilling. Die fehlende Symmetrie zwischen den Zwillingen wird noch deutlicher, wenn wir die Reise später in diesem Kapitel in Bezug auf den Weg, den die Astronautin durch die vierdimensionale Raumzeit zurücklegt, analysieren.
Im Jahr 1971 verifizierten die amerikanischen Physiker Joseph Hafele und Richard Keating die Zeitdilatation bei niedrigen Relativgeschwindigkeiten, indem sie extrem genaue Atomuhren in Verkehrsflugzeugen um die Welt flogen. Sie maßen die verstrichene Zeit mit einer Genauigkeit von wenigen Nanosekunden und verglichen sie mit der Zeit, die von zurückgelassenen Uhren gemessen wurde. Die Ergebnisse von Hafele und Keating lagen innerhalb der experimentellen Unsicherheiten der Vorhersagen der Relativitätstheorie. Sowohl die spezielle als auch die allgemeine Relativitätstheorie mussten berücksichtigt werden, da neben der Relativbewegung auch Gravitation und Beschleunigungen eine Rolle spielten.
Übung \(\PageIndex{2A}\)
a. Ein Teilchen bewegt sich mit \(1,90 \mal 10^8 \, m/s\) und lebt \(2,1 \mal 10^8 \, s\), wenn es relativ zu einem Beobachter ruht. Wie lange lebt das Teilchen, wenn man es im Labor betrachtet?
Antwort
Übung \(\PageIndex{2B}\)
Raumsonde A und B fliegen mit einer Relativgeschwindigkeit von \(4,00 \times 10^7 \, m/s\) in entgegengesetzter Richtung vorbei. Eine interne Uhr in Raumschiff A veranlasst es, ein Funksignal für 1,00 s auszusenden. Der Computer in Raumschiff B korrigiert, dass Anfang und Ende des Signals unterschiedliche Entfernungen zurückgelegt haben, um das Zeitintervall zu berechnen, in dem Raumschiff A das Signal ausgesendet hat. Welches Zeitintervall berechnet der Computer in Raumschiff B?
Antwort
Nur die relative Geschwindigkeit der beiden Raumschiffe spielt eine Rolle, da es keine absolute Bewegung durch den Raum gibt. Das Signal wird von einem festen Ort im Bezugssystem von A ausgesendet, also ist das richtige Zeitintervall seiner Aussendung \(\tau = 1,00 \, s\). Die Dauer des Signals, gemessen vom Bezugssystem B, ist dann
Beitragende und Zuschreibungen
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) und Bill Moebs mit vielen beitragenden Autoren. Dieses Werk ist lizenziert von OpenStax University Physics unter einer Creative Commons Attribution License (by 4.0).