Lernziele
Am Ende dieses Abschnitts werden Sie in der Lage sein:
- Erläutern Sie, was eine kontinuierliche Quell-Ladungsverteilung ist und wie sie mit dem Konzept der Quantisierung von Ladung zusammenhängt
- Beschreiben Sie Linienladungen, Oberflächenladungen und Volumenladungen
- Berechnen Sie das Feld einer kontinuierlichen Quell-Ladungsverteilung mit beliebigem Vorzeichen
Die Ladungsverteilungen, die wir bisher gesehen haben, waren diskret: Sie bestanden aus einzelnen Punktteilchen. Dies steht im Gegensatz zu einer kontinuierlichen Ladungsverteilung, die mindestens eine Dimension ungleich Null hat. Wenn eine Ladungsverteilung nicht diskret, sondern kontinuierlich ist, können wir die Definition des elektrischen Feldes verallgemeinern. Wir teilen die Ladung einfach in infinitesimale Stücke und behandeln jedes Stück als Punktladung.
Beachten Sie, dass es keine „wirklich“ kontinuierliche Ladungsverteilung gibt, da die Ladung quantisiert ist. In den meisten praktischen Fällen besteht die Gesamtladung, die das Feld erzeugt, jedoch aus einer so großen Anzahl von diskreten Ladungen, dass wir die diskrete Natur der Ladung getrost ignorieren und sie als kontinuierlich betrachten können. Das ist genau die Art von Annäherung, die wir machen, wenn wir einen Eimer Wasser als kontinuierliche Flüssigkeit betrachten und nicht als eine Ansammlung von \(\ce{H2O}\) Molekülen.
Unser erster Schritt ist die Definition einer Ladungsdichte für eine Ladungsverteilung entlang einer Linie, über eine Oberfläche oder innerhalb eines Volumens, wie in Abbildung \(\PageIndex{1}\).
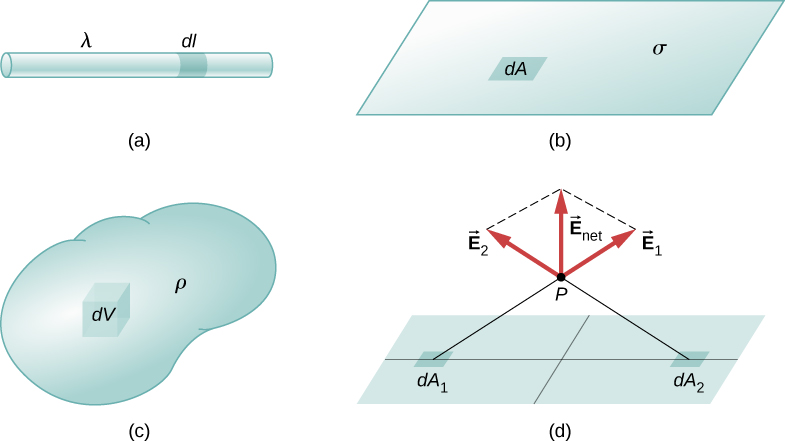
Definitionen: Ladungsdichten
Definitionen der Ladungsdichte:
- lineare Ladungsdichte: \(\lambda \equiv \) Ladung pro Längeneinheit (Abbildung \(\PageIndex{1a}\)); Einheiten sind Coulomb pro Meter (\(C/m\))
- Oberflächenladungsdichte: \(\sigma \equiv \) Ladung pro Flächeneinheit (Abbildung \(\PageIndex{1b}\)); Einheiten sind Coulomb pro Quadratmeter \((C/m^2)\)
- Volumenladungsdichte: \(\rho \equiv \) Ladung pro Volumeneinheit (Abbildung \(\PageIndex{1c}\)); Einheiten sind Coulomb pro Quadratmeter \((C/m^3)\)
Für eine Linienladung, eine Oberflächenladung und eine Volumenladung wird die Summation in der zuvor besprochenen Definition eines elektrischen Feldes zu einem Integral und \(q_i\) wird durch \(dq = \lambda dl\), \(\sigma dA\) bzw. \(\rho dV\) ersetzt:
\vec{E}(P) &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \int_{line} \left(\dfrac{\lambda \, dl}{r^2}\right) \hat{r}}_{\text{Line charge}} \label{eq2} \\vec{E}(P) &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \int_{surface} \left(\dfrac{\sigma \,dA}{r^2}\right) \hat{r} }_{\text{Surface charge}}\label{eq3} \\vec{E}(P) &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \int_{Volumen} \left(\dfrac{\rho \,dV}{r^2}\right) \hat{r}}_{\text{Volumenladung}} \label{eq4} \end{align}\]
Die Integrale in Gleichungen \ref{eq1}-\ref{eq4} sind Verallgemeinerungen des Ausdrucks für das Feld einer Punktladung. Sie beinhalten implizit das Superpositionsprinzip und setzen dieses voraus. Der „Trick“ bei ihrer Verwendung besteht fast immer darin, korrekte Ausdrücke für \(dl\), \(dA\) bzw. \(dV\) zu finden, die in Form von r ausgedrückt werden, und auch die Ladungsdichtefunktion angemessen auszudrücken. Sie kann konstant sein; sie kann ortsabhängig sein.
Beachten Sie sorgfältig die Bedeutung von \(r\) in diesen Gleichungen: Es ist der Abstand vom Ladungselement (\(q_i, \, \lambda \, dl, \, \sigma \, dA, \, \rho \, dV\)) zum Ort von Interesse, \(P(x, y, z)\) (der Punkt im Raum, an dem Sie das Feld bestimmen wollen). Verwechseln Sie dies jedoch nicht mit der Bedeutung von \(\hat{r}\); wir verwenden es und die Vektorschreibweise \(\vec{E}\), um drei Integrale auf einmal zu schreiben. Das heißt, Gleichung \ref{eq2} ist eigentlich
E_y(P) &= \dfrac{1}{4\pi \epsilon_0} \int_{line} \left(\dfrac{\lambda \, dl}{r^2}\right)_y, \\\ E_z(P) &= \dfrac{1}{4\pi \epsilon_0} \int_{line} \left(\dfrac{\lambda \, dl}{r^2}\right)_z \end{align} \]
Beispiel \(\PageIndex{1}\): Elektrisches Feld eines Liniensegments
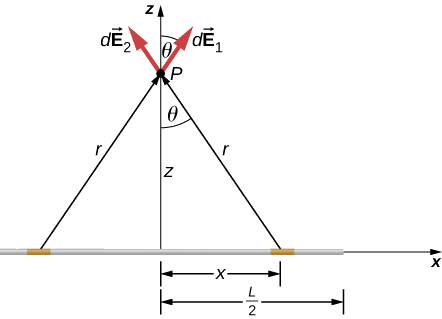
Bestimmen Sie das elektrische Feld in einem Abstand \(z\) über dem Mittelpunkt eines geraden Liniensegments der Länge \(L\), das eine gleichmäßige Linienladungsdichte \(\lambda\) trägt.
Strategie
Da es sich um eine kontinuierliche Ladungsverteilung handelt, zerlegen wir das Drahtsegment konzeptionell in differentielle Stücke der Länge \(dl\), von denen jedes eine differentielle Ladungsmenge trägt
Dann berechnen wir das differentielle Feld, das von zwei symmetrisch angeordneten Stücken des Drahtes erzeugt wird, wobei wir die Symmetrie des Aufbaus zur Vereinfachung der Berechnung nutzen (Abbildung \(\PageIndex{2}\)). Schließlich integrieren wir diesen Ausdruck für das Differentialfeld über die Länge des Drahtes (eigentlich über die Hälfte, wie wir unten erklären), um den vollständigen Ausdruck für das elektrische Feld zu erhalten.
Lösung
Bevor wir uns darauf stürzen, was erwarten wir, wie das Feld aus der Ferne „aussieht“? Da es ein endliches Liniensegment ist, sollte es aus der Ferne wie eine Punktladung aussehen. Wir überprüfen den Ausdruck, den wir erhalten, um zu sehen, ob er diese Erwartung erfüllt.
Das elektrische Feld für eine Linienladung ist durch den allgemeinen Ausdruck gegeben
Die Symmetrie der Situation (unsere Wahl der zwei identischen differentiellen Ladungsteile) impliziert, dass sich die horizontalen (x)-Komponenten des Feldes aufheben, so dass das Nettofeld in die \(z\)-Richtung zeigt. Überprüfen wir dies formal.
Das Gesamtfeld \(\vec{E}(P)\) ist die Vektorsumme der Felder von jedem der beiden Ladungselemente (nennen wir sie vorläufig \(\vec{E}_1\) und \(\vec{E}_2\)):
&= E_{1x}\hat{i} + E_{1z}\hat{k} + E_{2x} (-\hat{i}) + E_{2z}\hat{k}. \end{align*}\]
Da die beiden Ladungselemente identisch sind und den gleichen Abstand von dem Punkt \(P\) haben, an dem wir das Feld berechnen wollen, \(E_{1x} = E_{2x}\), heben sich diese Komponenten auf. Damit bleibt
&= E_1 \, \cos \, \theta \hat{k} + E_2 \, \cos \, \theta \hat{k}. \end{align*}\]
Diese Komponenten sind ebenfalls gleich, also haben wir
&= \dfrac{1}{4 \pi \epsilon_0}\int_0^{L/2} \dfrac{2\lambda dx}{r^2} \, \cos \, \theta \hat{k} \end{align*}\]
wobei unser Differentiallinienelement dl in diesem Beispiel dx ist, da wir entlang einer Ladungslinie integrieren, die auf der x-Achse liegt. (Die Grenzen der Integration sind 0 bis \(\frac{L}{2}\), nicht \(-\frac{L}{2}\) bis \(+\frac{L}{2}\), da wir das Netzfeld aus zwei differentiellen Ladungsstücken \(dq\) konstruiert haben. Würden wir über die gesamte Länge integrieren, bekämen wir fälschlicherweise den Faktor 2.)
Im Prinzip ist das vollständig. Um dieses Integral aber tatsächlich zu berechnen, müssen wir alle Variablen, die nicht gegeben sind, eliminieren. In diesem Fall ändern sich sowohl \(r\) als auch \(\theta\), wenn wir nach außen zum Ende der Linienladung integrieren, also sind das die Variablen, die wir loswerden müssen. Wir können das auf die gleiche Weise tun, wie wir es für die beiden Punktladungen getan haben: indem wir bemerken, dass
und
Substituieren, erhalten wir
&= \dfrac{1}{4 \pi \epsilon_0}\int_0^{L/2} \dfrac{2\lambda z}{(z^2 + x^2)^{3/2}} dx \hat{k} \\ &= \dfrac{2 \lambda z}{4 \pi \epsilon_0} \left_0^{L/2} \hat{k}. \end{align*}\]
Das vereinfacht sich zu
Bedeutung
Beachten Sie noch einmal die Verwendung der Symmetrie zur Vereinfachung des Problems. Dies ist eine sehr gängige Strategie zur Berechnung elektrischer Felder. Die Felder von unsymmetrischen Ladungsverteilungen müssen mit mehreren Integralen behandelt werden und müssen ggf. von einem Computer numerisch berechnet werden.
Wie würde sich die oben verwendete Strategie ändern, um das elektrische Feld an einem Punkt zu berechnen, der sich in einem Abstand \(z\) über einem Ende des endlichen Liniensegments befindet?
Antwort
Wir werden nicht mehr in der Lage sein, die Symmetrie zu nutzen. Stattdessen müssen wir jede der beiden Komponenten des elektrischen Feldes mit einem eigenen Integral berechnen.
Beispiel \(\PageIndex{2}\): Elektrisches Feld einer unendlichen Ladungslinie
Bestimmen Sie das elektrische Feld in einem Abstand \(z\) über dem Mittelpunkt einer unendlichen Ladungslinie, die eine gleichmäßige Linienladungsdichte \(\lambda\) trägt.
Strategie
Dies ist genau wie das vorangegangene Beispiel, nur dass die Grenzen der Integration \(-\infty\) bis \(+\infty\) sein werden.
Lösung
Auch hier heben sich die horizontalen Komponenten auf, sodass wir bei
in diesem Beispiel ist unser Differentiallinienelement dl dx, da wir entlang einer Ladungslinie integrieren, die auf der x-Achse liegt. Wiederum,
&= \dfrac{z}{(z^2 + x^2)^{1/2}}. \end{align*} \]
Substituieren wir, erhalten wir
&= \dfrac{1}{4 \pi \epsilon_0} \int_{-\infty}^{\infty} \dfrac{\lambda z}{(z^2 + x^2)^{3/2}}dx \hat{k} \\ &= \dfrac{1}{4 \pi \epsilon_0} \left_{-\infty}^{\infty} \, \hat{k} \end{align*}\]
Das vereinfacht sich zu
Bedeutung
Unsere Strategie für das Arbeiten mit kontinuierlichen Ladungsverteilungen liefert auch nützliche Ergebnisse für Ladungen mit unendlicher Dimension.
Im Fall einer endlichen Ladungslinie ist zu beachten, dass für \(z \gg L\), \(z^2\) das L im Nenner dominiert, so dass Gleichung12} sich vereinfacht zu
Wenn Sie sich daran erinnern, dass \(\lambda L = q\) die Gesamtladung auf dem Draht ist, haben wir den Ausdruck für das Feld einer Punktladung, wie erwartet, erhalten.
Im Grenzwert \(L \rightarrow \infty\) hingegen erhalten wir das Feld eines unendlichen geraden Drahtes, also eines geraden Drahtes, dessen Länge viel, viel größer ist als jede seiner anderen Dimensionen und auch viel, viel größer als der Abstand, in dem das Feld berechnet werden soll:
Ein interessantes Artefakt dieser unendlichen Grenze ist, dass wir die übliche \(1/r^2\)-Abhängigkeit verloren haben, an die wir gewöhnt sind. Dies wird im Fall einer unendlichen Ebene noch faszinierender.
Beispiel \(\PageIndex{3A}\): Elektrisches Feld durch einen Ring aus Ladung
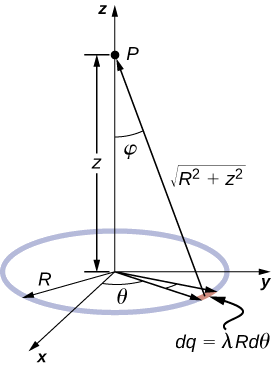
Ein Ring hat eine gleichmäßige Ladungsdichte \(\Lambda\), mit der Einheit Coulomb pro Einheitsmeter Bogenlänge. Finden Sie das elektrische Feld an einem Punkt auf der Achse, die durch den Mittelpunkt des Rings verläuft.
Strategie
Wir verwenden das gleiche Verfahren wie für den geladenen Draht. Der Unterschied ist hier, dass die Ladung auf einem Kreis verteilt ist. Wir unterteilen den Kreis in infinitesimale Elemente, die als Bögen auf dem Kreis geformt sind, und verwenden Polarkoordinaten, die in Abbildung \(\PageIndex{3}\) dargestellt sind.
Lösung
Das elektrische Feld für eine Linienladung ist gegeben durch den allgemeinen Ausdruck
A allgemeines Element des Bogens zwischen \(\theta\) und \(\theta + d\theta\) hat die Länge \(Rd\theta\) und enthält daher eine Ladung gleich \(\lambda R \,d\theta\). Das Element befindet sich in einem Abstand von \(r = \sqrt{z^2 + R^2}\) von \(P\), der Winkel ist \(\cos \, \phi = \dfrac{z}{\sqrt{z^2+R^2}}\) und daher ist das elektrische Feld
\ &= \dfrac{1}{4\pi \epsilon_0} \dfrac{\lambda Rz}{(z^2 + R^2)^{3/2}} \hat{z} \int_0^{2\pi} d\theta \\ &= \dfrac{1}{4\pi \epsilon_0} \dfrac{2\pi \lambda Rz}{(z^2 + R^2)^{3/2}} \hat{z} \\ &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}z}{(z^2 + R^2)^{3/2}} \hat{z}. \end{align*}\]
Bedeutung
Wie üblich, vereinfacht die Symmetrie dieses Problem und führt in diesem speziellen Fall zu einem trivialen Integral. Auch wenn wir den Grenzwert von \(z \gg R\) nehmen, finden wir, dass
wie wir erwarten.
Beispiel \(\PageIndex{3B}\): Das Feld einer Scheibe
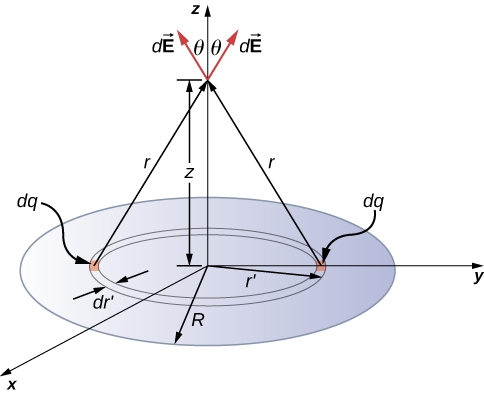
Bestimmen Sie das elektrische Feld einer kreisförmigen dünnen Scheibe mit Radius \(R\) und gleichmäßiger Ladungsdichte in einem Abstand \(z\) über dem Mittelpunkt der Scheibe (Abbildung \(\PageIndex{4}\))
Strategie
Das elektrische Feld für eine Oberflächenladung ist gegeben durch
Um Probleme mit Oberflächenladungen zu lösen, unterteilen wir die Oberfläche in symmetrische, differentielle „Streifen“, die der Form der Oberfläche entsprechen; hier verwenden wir Ringe, wie in der Abbildung gezeigt. Auch hier heben sich aufgrund der Symmetrie die horizontalen Komponenten auf, und das Feld verläuft vollständig in der vertikalen \((\hat{k})\) Richtung. Die vertikale Komponente des elektrischen Feldes wird durch Multiplikation mit \(\theta\) extrahiert, also
Wie zuvor müssen wir die unbekannten Faktoren im Integranden in Form der gegebenen Größen umschreiben. In diesem Fall
(Bitte beachten Sie die zwei verschiedenen „\(r\)’s“ hier; \(r\) ist der Abstand vom Differentialring der Ladung zu dem Punkt \(P\), wo wir das Feld bestimmen wollen, während \(r’\) der Abstand vom Zentrum der Scheibe zum Differentialring der Ladung ist). Außerdem haben wir bereits das Integral des Polarwinkels durchgeführt, indem wir \(dA\) aufgeschrieben haben.
Lösung
Setzen wir all dies ein, erhalten wir
&= \dfrac{1}{4 \pi \epsilon_0} \int_0^R \dfrac{\sigma (2\pi r‘ dr‘)z}{(r’^2 + z^2)^{3/2}} \hat{k} \\ &= \dfrac{1}{4 \pi \epsilon_0} (2\pi \sigma z)\left(\dfrac{1}{z} – \dfrac{1}{\sqrt{R^2 + z^2}}\right) \hat{k} \end{align*}\]
oder, einfacher ausgedrückt,
Bedeutung
Auch hier kann (über eine Taylor-Erweiterung) gezeigt werden, dass, wenn \(z \gg R\), dies reduziert wird auf
was der Ausdruck für eine Punktladung \(Q = \sigma \pi R^2\) ist.
Wie würde sich der obige Grenzwert bei einem gleichmäßig geladenen Rechteck statt einer Scheibe ändern?
Antwort
Die Punktladung wäre \(Q = \sigma ab\), wobei \(a\) und \(b\) die Seiten des Rechtecks sind, ansonsten aber identisch.
Als \(R \rightarrow \infty\) reduziert sich Gleichung \ref{5.14} auf das Feld einer unendlichen Ebene reduziert, die eine flache Platte ist, deren Fläche viel, viel größer als ihre Dicke ist, und auch viel, viel größer als der Abstand, in dem das Feld berechnet werden soll:
&= \dfrac{\sigma}{2 \epsilon_0} \hat{k}. \label{5.15} \end{align}\]
Beachten Sie, dass dieses Feld konstant ist. Dieses überraschende Ergebnis ist wiederum ein Artefakt unseres Grenzwerts, das wir aber in der Zukunft immer wieder verwenden werden. Um zu verstehen, warum dies geschieht, stellen Sie sich vor, Sie befänden sich über einer unendlichen Ebene mit konstanter Ladung. Sieht das Flugzeug anders aus, wenn Sie Ihre Höhe variieren? Nein – Sie sehen immer noch das Flugzeug, das ins Unendliche geht, egal wie weit Sie davon entfernt sind. Es ist wichtig zu beachten, dass Gleichung 5.15} deshalb gilt, weil wir uns oberhalb der Ebene befinden. Wären wir unten, würde das Feld in die Richtung \(- \hat{k}\) zeigen.
Beispiel \(\PageIndex{4}\): Das Feld zweier unendlicher Ebenen
Bestimmen Sie das elektrische Feld, das sich überall aus zwei unendlichen Ebenen mit gleicher, aber entgegengesetzter Ladungsdichte ergibt (Abbildung \(\PageIndex{5}\)).
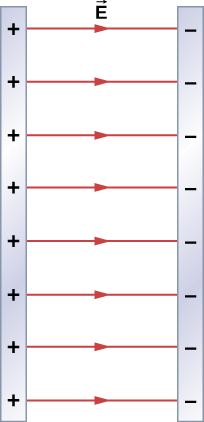
Strategie
Wir kennen bereits das elektrische Feld, das sich aus einer einzelnen unendlichen Ebene ergibt, also können wir das Überlagerungsprinzip verwenden, um das Feld von zwei zu finden.
Lösung
Das elektrische Feld zeigt von der positiv geladenen Ebene weg und zur negativ geladenen Ebene hin. Da sie gleich groß und entgegengesetzt sind, bedeutet dies, dass sich im Bereich außerhalb der beiden Ebenen die elektrischen Felder zu Null aufheben. Im Bereich zwischen den Ebenen addieren sich die elektrischen Felder jedoch, und wir erhalten
das elektrische Feld. Das liegt daran, dass in der Abbildung das Feld in die +x-Richtung zeigt.
Bedeutung
Systeme, die sich als zwei unendliche Ebenen dieser Art approximieren lassen, bieten eine nützliche Möglichkeit, gleichmäßige elektrische Felder zu erzeugen.
Wie würde das elektrische Feld in einem System mit zwei parallelen positiv geladenen Ebenen mit gleichen Ladungsdichten aussehen?
Antwort
Das elektrische Feld wäre dazwischen Null und hätte überall sonst die Größe \(\dfrac{\sigma}{\epsilon_0}\).
Mitwirkende und Zuschreibungen
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) und Bill Moebs mit vielen mitwirkenden Autoren. Dieses Werk ist lizenziert von OpenStax University Physics unter einer Creative Commons Attribution License (by 4.0).