Wie man mit abhängigen Ereignissen umgeht
Das Leben ist voll von zufälligen Ereignissen! Man muss ein „Gefühl“ für sie bekommen, um ein kluger und erfolgreicher Mensch zu sein.
Unabhängige Ereignisse
Ereignisse können „unabhängig“ sein, was bedeutet, dass jedes Ereignis nicht von anderen Ereignissen beeinflusst wird.

Beispiel: Der Wurf einer Münze.
Jeder Wurf einer Münze ist ein perfektes isoliertes Ding.
Was in der Vergangenheit geschah, hat keinen Einfluss auf den aktuellen Wurf.
Die Chance ist einfach 1:2 oder 50%, genau wie bei JEDEM Münzwurf.
So ist jeder Wurf ein unabhängiges Ereignis.
Abhängige Ereignisse
Aber Ereignisse können auch „abhängig“ sein … was bedeutet, dass sie von vorhergehenden Ereignissen beeinflusst werden können …

Beispiel: Murmeln in einem Beutel
2 blaue und 3 rote Murmeln befinden sich in einem Beutel.
Wie groß ist die Chance, eine blaue Murmel zu bekommen?
Die Chance ist 2 zu 5
Aber wenn man eine herausnimmt, ändert sich die Chance!
Also beim nächsten Mal:
Wenn wir vorher eine rote Murmel hatten, dann ist die Chance auf eine blaue Murmel beim nächsten Mal 2 zu 4
Wenn wir vorher eine blaue Murmel hatten, dann ist die Chance, dass wir als nächstes eine blaue Murmel bekommen, 1 zu 4
Das liegt daran, dass wir Murmeln aus dem Beutel entfernen.
Das nächste Ereignis hängt also davon ab, was im vorherigen Ereignis passiert ist, und wird als abhängig bezeichnet.
Ersetzung
Hinweis: Wenn wir die Murmeln im Beutel jedes Mal ersetzen, dann ändern sich die Chancen nicht und die Ereignisse sind unabhängig:
- Mit Ersetzung: Die Ereignisse sind unabhängig (die Chancen ändern sich nicht)
- Ohne Ersetzung: Die Ereignisse sind abhängig (die Chancen ändern sich)
Die abhängigen Ereignisse sind das, was wir hier betrachten.
Baumdiagramm
Ein Baumdiagramm: ist eine wunderbare Möglichkeit, sich die Vorgänge vorzustellen, also lassen Sie uns eines für unser Murmelbeispiel erstellen.
Es besteht eine 2/5 Chance, eine blaue Murmel herauszuziehen, und eine 3/5 Chance für Rot:
Wir können noch einen Schritt weiter gehen und sehen, was passiert, wenn wir eine zweite Murmel herausziehen:
Wenn zuerst eine blaue Murmel ausgewählt wurde, besteht nun eine 1/4 Chance, eine blaue Murmel zu bekommen und eine 3/4 Chance, eine rote Murmel zu bekommen.
Wenn eine rote Murmel zuerst ausgewählt wurde, besteht jetzt eine 2/4 Chance, eine blaue Murmel zu bekommen, und eine 2/4 Chance, eine rote Murmel zu bekommen.
Jetzt können wir Fragen beantworten wie „Wie groß ist die Chance, 2 blaue Murmeln zu ziehen?“
Antwort: Es ist eine 2/5 Chance, gefolgt von einer 1/4 Chance.
Haben Sie gesehen, wie wir die Chancen multipliziert haben? Und als Ergebnis 1/10 bekommen haben.
Die Wahrscheinlichkeit, 2 blaue Murmeln zu ziehen, ist 1/10
Notation
Wir lieben die Notation in der Mathematik! Es bedeutet, dass wir dann die Macht der Algebra nutzen können, um mit den Ideen herumzuspielen. Hier ist also die Notation für die Wahrscheinlichkeit:
P(A) bedeutet „Wahrscheinlichkeit des Ereignisses A“
In unserem Murmelbeispiel ist Ereignis A „zuerst eine blaue Murmel bekommen“ mit einer Wahrscheinlichkeit von 2/5:
P(A) = 2/5
Und Ereignis B ist „als zweites eine blaue Murmel bekommen“ … aber dafür haben wir 2 Möglichkeiten:
- Wenn wir zuerst eine blaue Murmel bekommen, ist die Chance jetzt 1/4
- Wenn wir zuerst eine rote Murmel bekommen, ist die Chance jetzt 2/4
So müssen wir sagen, welche wir wollen, und das Symbol „|“ für „gegeben“ verwenden:
P(B|A) bedeutet „Ereignis B gegeben Ereignis A“
Mit anderen Worten: Ereignis A ist bereits eingetreten, wie groß ist nun die Chance auf Ereignis B?
P(B|A) wird auch die „Bedingte Wahrscheinlichkeit“ von B bei A genannt.
Und in unserem Fall:
P(B|A) = 1/4
Die Wahrscheinlichkeit, 2 blaue Murmeln zu bekommen, ist also:
Und wir schreiben es als
„Die Wahrscheinlichkeit des Ereignisses A und des Ereignisses B ist gleich
der Wahrscheinlichkeit des Ereignisses A mal der Wahrscheinlichkeit des Ereignisses B bei Ereignis A“
Lassen Sie uns das nächste Beispiel nur in der Notation durchführen:
Beispiel: Ziehen von 2 Königen aus einem Deck
Ereignis A ist das Ziehen eines Königs als erstes, und Ereignis B ist das Ziehen eines Königs als zweites.
Für die erste Karte ist die Wahrscheinlichkeit, einen König zu ziehen, 4 aus 52 (es gibt 4 Könige in einem Deck von 52 Karten):
P(A) = 4/52
Nach dem Entfernen eines Königs aus dem Deck ist die Wahrscheinlichkeit, dass die zweite gezogene Karte ein König ist, jedoch geringer (nur 3 der 51 verbleibenden Karten sind Könige):
P(B|A) = 3/51
Und so:
P(A und B) = P(A) x P(B|A) =(4/52)x (3/51) = 12/2652 = 1/221
Die Chance, 2 Könige zu bekommen, ist also 1 zu 221, also etwa 0.5%
Finden versteckter Daten
Mit Hilfe der Algebra können wir auch das „Thema“ der Formel ändern, etwa so:
| Beginnen Sie mit: | P(A und B) = P(A) x P(B|A) | |
| Seiten tauschen: | P(A) x P(B|A) = P(A und B) | |
| Division durch P(A): | P(B|A) = P(A und B) / P(A) |
Und wir haben eine weitere nützliche Formel:
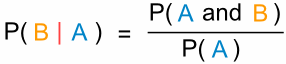
„Die Wahrscheinlichkeit des Ereignisses B bei Ereignis A ist gleich
der Wahrscheinlichkeit von Ereignis A und Ereignis B geteilt durch die Wahrscheinlichkeit von Ereignis A
Beispiel: Eiscreme
70% Ihrer Freunde mögen Schokolade, und 35% mögen Schokolade UND mögen Erdbeere.
Wie viel Prozent derjenigen, die Schokolade mögen, mögen auch Erdbeere?
P(Erdbeere|Schokolade) = P(Schokolade und Erdbeere) / P(Schokolade)
50 % Ihrer Freunde, die Schokolade mögen, mögen auch Erdbeere

Big Example: Fußballspiel
Du bist auf dem Weg zum Fußball und möchtest der Torwart sein, aber das hängt davon ab, wer heute der Trainer ist:
- Bei Trainer Sam ist die Wahrscheinlichkeit, Torwart zu sein, 0,5
- Bei Trainer Alex ist die Wahrscheinlichkeit, Torwart zu sein, 0.3
Sam ist häufiger Trainer … etwa 6 von 10 Spielen (eine Wahrscheinlichkeit von 0,6).
So, wie hoch ist die Wahrscheinlichkeit, dass Sie heute Torwart sind?
Lassen Sie uns ein Baumdiagramm erstellen. Zuerst zeigen wir die beiden möglichen Trainer: Sam oder Alex:
Die Wahrscheinlichkeit, Sam zu bekommen, ist 0,6, also muss die Wahrscheinlichkeit, Alex zu bekommen, 0,4 sein (zusammen ist die Wahrscheinlichkeit 1)
Nun, wenn Sie Sam bekommen, gibt es eine Wahrscheinlichkeit von 0,5, Goalie zu sein (und 0.5, nicht Goalie zu sein):
Wenn man Alex bekommt, gibt es 0,3 Wahrscheinlichkeit, Goalie zu sein (und 0.7 nicht):
Das Baumdiagramm ist vollständig, nun wollen wir die Gesamtwahrscheinlichkeiten berechnen. Erinnern Sie sich daran:
P(A und B) = P(A) x P(B|A)
Hier ist, wie man es für den „Sam, Ja“-Zweig macht:
(Wenn wir die 0.6 Chance, dass Sam Trainer ist, mal die 0,5 Chance, dass Sam dich Torwart sein lässt, kommen wir auf eine 0,3 Chance.)
Aber wir sind noch nicht fertig! Wir haben Alex als Trainer nicht mit einbezogen:
Eine Chance von 0,4, dass Alex Trainer ist, gefolgt von einer Chance von 0,3 ergibt 0,12
Und die beiden „Ja“-Zweige des Baums ergeben zusammen:
0,3 + 0,12 = 0.42 Wahrscheinlichkeit, heute ein Torwart zu sein
(Das ist eine 42%ige Chance)
Kontrolle
Ein letzter Schritt: Vervollständigen Sie die Berechnungen und stellen Sie sicher, dass sie sich zu 1 addieren:
0.3 + 0,3 + 0,12 + 0,28 = 1
Ja, sie addieren sich zu 1, das sieht also richtig aus.
Freunde und Zufallszahlen
Hier ist ein ganz anderes Beispiel für bedingte Wahrscheinlichkeit.
4 Freunde (Alex, Blake, Chris und Dusty) wählen jeweils eine Zufallszahl zwischen 1 und 5. Wie groß ist die Chance, dass einer von ihnen die gleiche Zahl gewählt hat?
Lassen Sie uns unsere Freunde einzeln hinzufügen …
Erstens, wie groß ist die Chance, dass Alex und Blake die gleiche Zahl haben?
Blake vergleicht seine Zahl mit Alex‘ Zahl. Die Chance, dass sie übereinstimmen, liegt bei 1:5.
Als Baumdiagramm:
Anmerkung: „Ja“ und „Nein“ ergeben zusammen 1
(1/5 + 4/5 = 5/5 = 1)
Nun nehmen wir Chris dazu …
Jetzt gibt es aber zwei Fälle zu berücksichtigen:
- Wenn Alex und Blake übereinstimmten, dann hat Chris nur eine Zahl zum Vergleich.
- Wenn Alex und Blake aber nicht übereinstimmten, dann hat Chris zwei Zahlen zum Vergleich.
Und wir erhalten folgendes:
Für die obere Zeile (Alex und Blake haben übereingestimmt) haben wir bereits eine Übereinstimmung (eine Chance von 1/5).
Aber für „Alex und Blake haben nicht übereingestimmt“ gibt es jetzt eine 2/5 Chance, dass Chris übereinstimmt (weil Chris seine Nummer sowohl gegen Alex als auch gegen Blake abgleichen kann).
Und wir können die kombinierte Chance berechnen, indem wir die Chancen multiplizieren, die nötig waren, um dorthin zu gelangen:
Bei dem Pfad „Nein, Ja“ … gibt es eine 4/5 Chance auf Nein, gefolgt von einer 2/5 Chance auf Ja:
Bei dem Pfad „Nein, Nein“ …. gibt es eine 4/5 Chance auf „Nein“, gefolgt von einer 3/5 Chance auf „Nein“:
Beachten Sie auch, dass wir, wenn wir alle Chancen zusammenzählen, immer noch 1 erhalten (eine gute Überprüfung, dass wir keinen Fehler gemacht haben):
(5/25) + (8/25) + (12/25) = 25/25 = 1
Was passiert nun, wenn wir Dusty einbeziehen?
Es ist die gleiche Idee, nur mehr davon:
OK, das sind alle 4 Freunde, und die „Ja“-Chancen ergeben zusammen 101/125:
Antwort: 101/125
Aber hier ist etwas Interessantes … wenn wir dem „Nein“-Pfad folgen, können wir alle anderen Berechnungen überspringen und uns das Leben leichter machen:
Die Chancen auf Nichtübereinstimmung sind:
(4/5) × (3/5) × (2/5) = 24/125
Die Chancen auf Übereinstimmung sind also:
1 – (24/125) = 101/125
(Und dafür brauchten wir nicht wirklich ein Baumdiagramm!)
















