Mobilen Hinweis anzeigen Alle Hinweise anzeigen Alle Hinweise ausblenden
Abschnitt 1-12 : Zylindrische Koordinaten
Wie im zweidimensionalen Raum wird das Standard-Koordinatensystem \(\left( {x,y,z} \right)\) als kartesisches Koordinatensystem bezeichnet. In den letzten beiden Abschnitten dieses Kapitels werden wir uns einige alternative Koordinatensysteme für den dreidimensionalen Raum ansehen.
Wir beginnen mit dem zylindrischen Koordinatensystem. Dieses ist recht einfach, da es nichts anderes als eine Erweiterung der Polarkoordinaten in drei Dimensionen ist. Es ist nicht nur eine Erweiterung von Polarkoordinaten, sondern wir erweitern es in die dritte Dimension, genauso wie wir kartesische Koordinaten in die dritte Dimension erweitern. Alles, was wir tun, ist, ein \(z\) als dritte Koordinate hinzuzufügen. Die \(r\) und \(\theta\) sind die gleichen wie bei Polarkoordinaten.
Hier ist eine Skizze eines Punktes in \({\mathbb{R}^3}\).
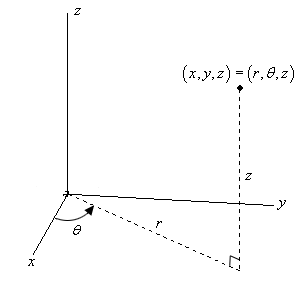
Die Umrechnungen für \(x\) und \(y\) sind die gleichen Umrechnungen, die wir schon bei der Betrachtung von Polarkoordinaten verwendet haben. Wenn wir also einen Punkt in zylindrischen Koordinaten haben, können die kartesischen Koordinaten mit den folgenden Umrechnungen gefunden werden.
Die dritte Gleichung ist nur eine Bestätigung dafür, dass die \(z\)-Koordinate eines Punktes in kartesischen und polaren Koordinaten die gleiche ist.
Gleichermaßen können wir, wenn wir einen Punkt in kartesischen Koordinaten haben, die zylindrischen Koordinaten mit Hilfe der folgenden Umrechnungen finden.
Lassen Sie uns einen kurzen Blick auf einige Flächen in zylindrischen Koordinaten werfen.
- \(r = 5\)
- \({r^2} + {z^2} = 100\)
- \(z = r\)
Alle Lösungen anzeigen Alle Lösungen ausblenden
In zwei Dimensionen wissen wir, dass dies ein Kreis mit Radius 5 ist. Da wir uns nun in drei Dimensionen befinden und kein \(z\) in der Gleichung steht, bedeutet dies, dass sie frei variieren darf. Also werden wir für jedes gegebene \(z\) einen Kreis mit Radius 5 haben, der auf der \(z\)-Achse zentriert ist.
Mit anderen Worten, wir werden einen Zylinder mit Radius 5 haben, der auf der \(z\)-Achse zentriert ist.
b \({r^2} + {z^2} = 100\) Lösung anzeigen
Diese Gleichung ist leicht zu erkennen, wenn wir wieder in kartesische Koordinaten umrechnen.
Es handelt sich also um eine im Ursprung zentrierte Kugel mit dem Radius 10.
c \(z = r\) Lösung anzeigen
Auch diese Gleichung ist leicht zu erkennen, wenn wir wieder in kartesische Koordinaten umrechnen. Aus Gründen, die wir später noch sehen werden, quadrieren wir erst beide Seiten und konvertieren dann.
\
Aus dem Abschnitt über quadratische Flächen wissen wir, dass dies die Gleichung eines Kegels ist.