Was ist die gemeinsame Wahrscheinlichkeit?
Die gemeinsame Wahrscheinlichkeit ist ein Maß, das durch die Berechnung der Wahrscheinlichkeit des gleichzeitigen Auftretens zweier Ereignisse ermittelt wird. Mit anderen Worten, es ist die Wahrscheinlichkeit, dass das Ereignis X zur gleichen Zeit wie das Ereignis Y eintritt, wie ein Schnittpunkt zweier Ereignisse.
Gemeinsame Wahrscheinlichkeit für abhängige Ereignisse
Um die gemeinsame Wahrscheinlichkeit zu messen, müssen beide Ereignisse zur gleichen Zeit eintreten und unabhängig voneinander sein. Das bedeutet, dass die gemeinsame Wahrscheinlichkeit für abhängige Ereignisse nicht bestimmt werden kann.
Angenommen, Sie wollen bestimmen, ob es zur gleichen Zeit regnen wird, wenn Wolken am Himmel sind. Diese beiden Ereignisse sind voneinander abhängig, denn wenn es regnet, sind höchstwahrscheinlich auch Wolken vorhanden. Daher sind diese Ereignisse voneinander abhängig.
Anstatt der gemeinsamen Wahrscheinlichkeit sollte die bedingte Wahrscheinlichkeit für abhängige Ereignisse verwendet werden.
Gemeinsame Wahrscheinlichkeit für unabhängige Ereignisse
Wie bereits erwähnt, müssen zur Bestimmung der gemeinsamen Wahrscheinlichkeit beide Ereignisse unabhängig voneinander sein. Zum Beispiel sind die Wahrscheinlichkeiten, bei einem Münzwurf „Zahl“ oder „Kopf“ zu erhalten, unabhängige Ereignisse. Mit anderen Worten: Die Wahrscheinlichkeit, beim ersten Wurf „Zahl“ zu erhalten, hat keinen Einfluss auf die Wahrscheinlichkeit, „Kopf“ zu erhalten, wenn man die Münze ein zweites Mal wirft.
Berechnung der gemeinsamen Wahrscheinlichkeit
Wenn Sie lernen, wie man die gemeinsame Wahrscheinlichkeit berechnet, ist es wichtig zu verstehen, dass die Formel voraussetzt, dass die beiden Ereignisse unabhängig voneinander sind. Das bedeutet, dass der Ausgang eines Ereignisses keinen Einfluss auf den Ausgang des anderen Ereignisses haben darf. Bevor Sie die gemeinsame Wahrscheinlichkeit berechnen, sollten Sie sich fragen, ob das Ergebnis des einen Ereignisses das Ergebnis des anderen beeinflussen wird.
Da die gemeinsame Wahrscheinlichkeit als „Schnittpunkt zweier Ereignisse“ beschrieben werden kann, wird die Formel die beiden einbeziehen – und wie sie sich überschneiden können.
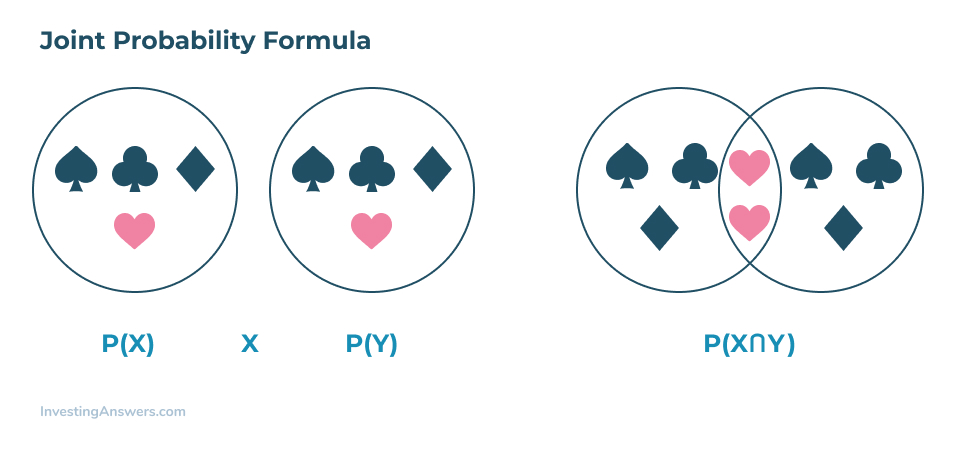
In der untenstehenden Formel sehen Sie das Symbol „∩“, das eine Schnittmenge darstellt. Für visuellere Lernende ist die Verwendung eines Venn-Diagramms die beste Möglichkeit, um zu veranschaulichen, wie sich zwei Ereignisse überschneiden können.
Gemeinsame Wahrscheinlichkeitsformel
Die gemeinsame Wahrscheinlichkeitsformel lautet wie folgt:
In dieser Formel stellen X und Y zwei verschiedene Ereignisse dar, die sich überschneiden, und P ist gleich der Verbindungswahrscheinlichkeit von sowohl X als auch Y.
Andere Möglichkeiten, die gemeinsame Wahrscheinlichkeitsformel auszudrücken, sind auch P( X und Y) und P(XY).
Beispiel 1 für die gemeinsame Wahrscheinlichkeit
Angenommen, Sie möchten die gemeinsame Wahrscheinlichkeit für einen Münzwurf ermitteln, bei dem Sie eine Zahl (Ereignis X) gefolgt von einer Zahl (Ereignis Y) erhalten können.
In diesem Fall ist die Wahrscheinlichkeit für das Ereignis X 50 % (oder 0,5) und die Wahrscheinlichkeit für das Ereignis Y ist ebenfalls 50 %. Jetzt können wir die Zahlen in die Formel einsetzen:
P(0,5 x 0,5) = 0,25 oder 25%
Das bedeutet, dass die gemeinsame Wahrscheinlichkeit, bei einem Münzwurf eine Zahl mit Schwanz und dann eine mit Kopf zu erhalten, 25% beträgt.
Beispiel für gemeinsame Wahrscheinlichkeit #2
Sie würfeln und wollen die gemeinsame Wahrscheinlichkeit herausfinden, zweimal hintereinander die Zahl sechs zu würfeln. Die Wahrscheinlichkeit, beim ersten Mal eine Sechs zu würfeln, ist 1/6, da ein sechsseitiger Würfel nur sechs Möglichkeiten hat. Das entspricht ⅙ oder 17 % (in Dezimalzahlen sind das 0,1666). Dasselbe gilt für den zweiten Wurf einer Sechs.
Anhand dieser Informationen können wir feststellen, dass die gemeinsame Wahrscheinlichkeit, beim ersten und zweiten Mal eine Sechs zu würfeln, wie folgt ist:
P(0,1666 x 0,1666) = 0,02777 oder 2,8 %
Das bedeutet, dass die Wahrscheinlichkeit, dass beide Ereignisse eintreten, 2,8 % beträgt.
Wann verwendet man die gemeinsame Wahrscheinlichkeit
Die gemeinsame Wahrscheinlichkeit ist nützlich, wenn man zwei unabhängige Ereignisse messen möchte, um festzustellen, ob sie gleichzeitig eintreten können.
Wie wird die gemeinsame Wahrscheinlichkeit in Bezug auf das Investieren verwendet?
Die gemeinsame Wahrscheinlichkeit ist eine nützliche Statistik für Analysten und Statistiker, wenn zwei oder mehr beobachtbare Phänomene gleichzeitig auftreten können. Zum Beispiel, wenn ein Rückgang des Dow Jones Industrial Average mit einem erheblichen Wertverlust des Dollars einhergeht.
Sie können auch zwei separate Aktien vergleichen, um zu sehen, ob der Wert der einen steigt (und ob die andere auch steigt).