„Grad“ kann in der Mathematik mehrere Dinge bedeuten:
- In der Geometrie ist ein Grad (°) eine Art, Winkel zu messen,
- Aber hier schauen wir uns an, was Grad in der Algebra bedeutet.
In der Algebra wird „Grad“ manchmal „Ordnung“ genannt.
Grad eines Polynoms (mit einer Variablen)
Ein Polynom sieht so aus:
Beispiel für ein Polynom
dieses hat 3 Terme
der größte Exponent dieser Variablen.
Weitere Beispiele:
| 4x | Der Grad ist 1 (eine Variable ohne Exponent hat tatsächlich einen Exponenten von 1) |
|
| 4×3 – x + 3 | Der Grad ist 3 (größter Exponent von x) | |
| x2 + 2×5 – x | Der Grad ist 5 (größter Exponent von x) | |
| z2 – z + 3 | Der Grad ist 2 (größter Exponent von z) |
Namen von Graden
Wenn wir den Grad kennen, können wir ihm auch einen Namen geben!
| Degree | Name | Beispiel |
|---|---|---|
| 0 | Konstant | 7 |
| 1 | Linear | x+3 |
| 2 | Quadratisch | x2-x+2 |
| 3 | Kubisch | x3-x2+5 |
| 4 | Quartisch | 6×4-x3+x-2 |
| 5 | Quintisch | x5-3×3+x2+8 |
Beispiel: y = 2x + 7 hat einen Grad von 1, ist also eine lineare Gleichung
Beispiel: 5w2 – 3 hat den Grad 2, ist also quadratisch
Gleichungen höherer Ordnung sind meist schwieriger zu lösen:
- Lineare Gleichungen sind leicht zu lösen
- Quadratische Gleichungen sind etwas schwieriger zu lösen
- Kubische Gleichungen sind wieder schwieriger, aber es gibt Formeln, die helfen
- Quartische Gleichungen können auch gelöst werden, aber die Formeln sind sehr kompliziert
- Quintische Gleichungen haben keine Formeln und können manchmal unlösbar sein!
Grad eines Polynoms mit mehr als einer Variablen
Wenn ein Polynom mehr als eine Variable hat, müssen wir uns jeden Term ansehen. Terme werden durch + oder – Zeichen getrennt:
Beispiel für ein Polynom
mit mehr als einer Variablen
Für jeden Term:
- Ermitteln Sie den Grad, indem Sie die Exponenten jeder Variablen darin addieren,
Der größte dieser Grade ist der Grad des Polynoms.
Beispiel: Wie lautet der Grad dieses Polynoms:
Prüfen Sie jeden Term:
- 5xy2 hat den Grad 3 (x hat einen Exponenten von 1, y hat 2, und 1+2=3)
- 3x hat einen Grad von 1 (x hat einen Exponenten von 1)
- 5y3 hat einen Grad von 3 (y hat einen Exponenten von 3)
- 3 hat einen Grad von 0 (keine Variable)
Der größte Grad davon ist 3 (tatsächlich haben zwei Terme einen Grad von 3), also hat das Polynom einen Grad von 3
Beispiel: Was ist der Grad dieses Polynoms:
4z3 + 5y2z2 + 2yz
Prüfen Sie jeden Term:
- 4z3 hat den Grad 3 (z hat einen Exponenten von 3)
- 5y2z2 hat den Grad 4 (y hat einen Exponenten von 2, z hat 2, und 2+2=4)
- 2yz hat den Grad 2 (y hat einen Exponenten von 1, z hat 1, und 1+1=2)
Der größte Grad davon ist 4, also hat das Polynom einen Grad von 4
Ausschreiben
Anstatt zu sagen „der Grad von (was auch immer) ist 3“ schreiben wir es so:
Wenn der Ausdruck ein Bruch ist
Wir können den Grad eines rationalen Ausdrucks (der in Form eines Bruchs vorliegt) berechnen, indem wir den Grad des oberen Teils (Zähler) nehmen und den Grad des unteren Teils (Nenner) subtrahieren.
Hier sind drei Beispiele:
Berechnen anderer Arten von Ausdrücken
Warnung: Advanced Ideas Ahead!
Den Grad eines Ausdrucks können wir manchmal berechnen, indem wir …
- den Logarithmus der Funktion durch
- den Logarithmus der Variablen
… und das dann für immer größere Werte tun, um zu sehen, wohin die Antwort „geht“.
(Korrekter wäre es, die Grenze zur Unendlichkeit von ln(f(x))/ln(x) zu berechnen, aber ich will das hier einfach halten).
|
Hinweis: „ln“ ist die natürliche Logarithmusfunktion. |
 |
Hier ein Beispiel:
Beispiel: Was ist der Grad von (3 plus die Quadratwurzel aus x)?
Lassen Sie uns versuchen, die Werte von x zu erhöhen:
| x | ln( ) |
ln(x) | ln() / ln(x) |
|---|---|---|---|
| 2 | 1.48483 | 0.69315 | 2.1422 |
| 4 | 1.60944 | 1.38629 | 1.1610 |
| 10 | 1.81845 | 2.30259 | 0.7897 |
| 100 | 2.56495 | 4.60517 | 0.5570 |
| 1.000 | 3.54451 | 6.90776 | 0.5131 |
| 10.000 | 4.63473 | 9.21034 | 0.5032 |
| 100.000 | 5.76590 | 11.51293 | 0.5008 |
| 1.000.000 | 6.91075 | 13.81551 | 0.5002 |
Betrachtet man die Tabelle:
- Wenn x größer wird, dann wird ln(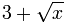) / ln(x) immer näher an 0,5 heran
So ist der Grad 0.5 (mit anderen Worten 1/2)
(Anmerkung: Dies stimmt gut mit x½ = Quadratwurzel aus x überein, siehe Fractional Exponents)
Einige Gradwerte
| Ausdruck | Grad |
|---|---|
| log(x) | 0 |
| ex | ∞ |
| 1/x | -1 |
 |
1/2 |