Die Berechnungen der PPT erfolgen in der E-Ebene, d. h. das Laserfeld wird als elektromagnetische Wellen aufgefasst. Die Ionisationsrate kann auch in der A-Ebene berechnet werden, was die Teilchennatur des Lichts betont (Absorption mehrerer Photonen während der Ionisation). Dieser Ansatz wurde vom Krainov-Modell übernommen, das auf den früheren Arbeiten von Faisal und Reiss basiert. Die resultierende Rate ist gegeben durch
W K R A = ∑ n = N ∞ 2 π ω 2 p ( n – n o s c ) 2 ∫ d Ω | F T ( I K A R Ψ ( r ) ) | 2 J n 2 ( n f , n o s c 2 ) {\displaystyle W_{KRA}=\sum _{n=N}^{\infty }2\pi \omega ^{2}p\left(n-n_{\mathrm {osc} }\right)^{2}\int \mathrm {d} \Omega \left|FT\left(I_{KAR}\Psi \left(\mathbf {r} \right)\right|^{2}J_{n}^{2}\left(n_{f},{\frac {n_{\mathrm {osc} }}{2}}\right)}

wo:
- n i = E i / ω , {\displaystyle n_{i}=E_{i}/\omega ,}
- n o s c = U p / ω {\displaystyle n_{{\mathrm {osc} }=U_{p}/\omega }
mit U p {\displaystyle U_{p}}
die ponderomotorische Energie ist,
- N = {\displaystyle N=}
ist die minimale Anzahl von Photonen, die notwendig ist, um das Atom zu ionisieren,
- J n ( u , v ) {\displaystyle J_{n}(u,v)}
ist die Doppel-Bessel-Funktion,
- p = 2 ω ( n – n o s c – n i ) , {\displaystyle p={\sqrt {2\omega (n-n_{\mathrm {osc} }-n_{i})}},}
- n f = 2 n o s c / ω p cos ( θ ) {\displaystyle n_{f}=2{\sqrt {n_{\mathrm {osc} }/\omega }}p\cos(\theta )}
mit θ {\displaystyle \theta }
der Winkel zwischen dem Impuls des Elektrons, p, und dem elektrischen Feld des Lasers, F,
- FT ist die dreidimensionale Fouriertransformation, und
- I K A R = ( 2 Z 2 n 2 F r ) n {\displaystyle I_{KAR}=\left({\frac {2Z^{2}}{n^{2}Fr}}\right)^{n}}
beinhaltet die Coulomb-Korrektur im SFA-Modell.
Atomstabilisierung/PopulationseinfangBearbeiten
Bei der Berechnung der MPI-Rate von Atomen werden nur Übergänge in die Kontinuumszustände berücksichtigt. Eine solche Näherung ist akzeptabel, solange es keine Multiphotonenresonanz zwischen dem Grundzustand und einigen angeregten Zuständen gibt. In der realen Situation der Wechselwirkung mit gepulsten Lasern besteht jedoch während der Entwicklung der Laserintensität aufgrund der unterschiedlichen Stark-Verschiebung der Grund- und angeregten Zustände die Möglichkeit, dass einige angeregte Zustände in Mehrphotonenresonanz mit dem Grundzustand gehen. Im Rahmen des Dressed-Atom-Bildes wird der Grundzustand mit m {\displaystyle m}

Photonen und der Resonanzzustand eine vermiedene Kreuzung bei der Resonanzintensität I r {\displaystyle I_{r}}

. Der minimale Abstand, V m {\displaystyle V_{m}}

, beim vermiedenen Übergang ist proportional zur verallgemeinerten Rabi-Frequenz, Γ ( t ) = Γ m I ( t ) m / 2 {\displaystyle \Gamma (t)=\Gamma _{m}I(t)^{m/2}}

die beiden Zustände koppelt. Nach Story et al. ist die Wahrscheinlichkeit, im Grundzustand zu bleiben, P g {\displaystyle P_{g}}

, ist gegeben durch P g = exp ( – 2 π W m 2 d W / d t ) {\displaystyle P_{g}=\exp \left(-{\frac {2\pi W_{m}^{2}}{\mathrm {d} W/\mathrm {d} t}}\right)}

wobei W {\displaystyle W}

ist die zeitabhängige Energiedifferenz zwischen den beiden dressed Zuständen. Wird bei der Wechselwirkung mit einem kurzen Puls die dynamische Resonanz im ansteigenden oder abfallenden Teil des Pulses erreicht, verbleibt die Population praktisch im Grundzustand und der Effekt der Mehrphotonenresonanzen kann vernachlässigt werden. Wenn die Zustände jedoch in der Spitze des Pulses in Resonanz gehen, wo d W / d t = 0 {\displaystyle \mathrm {d} W/\mathrm {d} t=0}

, dann ist der angeregte Zustand besiedelt. Da das Ionisationspotential des angeregten Zustands klein ist, wird erwartet, dass das Elektron nach der Besiedlung sofort ionisiert wird.
Im Jahr 1992 zeigten de Boer und Muller, dass Xe-Atome, die kurzen Laserpulsen ausgesetzt wurden, in den hoch angeregten Zuständen 4f, 5f und 6f überleben konnten. Man nahm an, dass diese Zustände durch die dynamische Stark-Verschiebung der Niveaus in Mehrphotonenresonanz mit dem Feld während des ansteigenden Teils des Laserpulses angeregt wurden. Die nachfolgende Entwicklung des Laserpulses hat diese Zustände nicht vollständig ionisiert und einige hoch angeregte Atome zurückgelassen. Wir bezeichnen dieses Phänomen als „Populationsfalle“.

Wir erwähnen die theoretische Berechnung, dass unvollständige Ionisation immer dann auftritt, wenn es eine parallele resonante Anregung in ein gemeinsames Niveau mit Ionisationsverlust gibt. Wir betrachten einen Zustand wie 6f von Xe, der aus 7 quasi-degnerischen Niveaus im Bereich der Laserbandbreite besteht. Diese Niveaus bilden zusammen mit dem Kontinuum ein Lambda-System. Der Mechanismus des Lambda-Fallens ist in der Abbildung schematisch dargestellt. Im ansteigenden Teil des Pulses (a) befindet sich der angeregte Zustand (mit zwei entarteten Niveaus 1 und 2) nicht in Multiphotonenresonanz mit dem Grundzustand. Das Elektron wird durch Multiphotonenkopplung mit dem Kontinuum ionisiert. Wenn die Intensität des Pulses erhöht wird, werden der angeregte Zustand und das Kontinuum aufgrund der Stark-Verschiebung in der Energie verschoben. Bei der Spitze des Pulses (b) gehen die angeregten Zustände in Multiphotonenresonanz mit dem Grundzustand. Wenn die Intensität abnimmt (c), werden die beiden Zustände durch das Kontinuum gekoppelt und die Population ist in einer kohärenten Überlagerung der beiden Zustände gefangen. Unter der nachfolgenden Einwirkung desselben Pulses kann das Feld aufgrund von Interferenzen in den Übergangsamplituden des Lambda-Systems die Population nicht vollständig ionisieren und ein Teil der Population wird in einer kohärenten Überlagerung der quasi entarteten Niveaus gefangen sein. Nach dieser Erklärung würden die Zustände mit höherem Drehimpuls – mit mehr Subniveaus – eine höhere Wahrscheinlichkeit für das Einfangen der Population haben. Im Allgemeinen wird die Stärke des Einfangens durch die Stärke der Zwei-Photonen-Kopplung zwischen den quasi-entarteten Niveaus über das Kontinuum bestimmt. 1996 beobachteten Talebpour et al. unter Verwendung eines sehr stabilen Lasers und unter Minimierung der Maskierungseffekte der Ausdehnung des Fokusbereichs mit zunehmender Intensität Strukturen auf den Kurven von einfach geladenen Ionen von Xe, Kr und Ar. Diese Strukturen wurden auf Elektroneneinfang im starken Laserfeld zurückgeführt. Eine eindeutigere Demonstration von Populationseinfang wurde von T. Morishita und C. D. Lin berichtet.
Nichtsequenzielle MehrfachionisationBearbeiten
Das Phänomen der nichtsequenziellen Ionisation (NSI) von Atomen, die intensiven Laserfeldern ausgesetzt sind, ist seit 1983 Gegenstand vieler theoretischer und experimenteller Studien. Die Pionierarbeit begann mit der Beobachtung einer „Knie“-Struktur auf der Xe2+-Ionensignal-gegen-Intensität-Kurve durch L’Huillier et al. Aus experimenteller Sicht bezieht sich die NS-Doppelionisation auf Prozesse, die irgendwie die Produktionsrate von doppelt geladenen Ionen um einen großen Faktor bei Intensitäten unterhalb der Sättigungsintensität des einfach geladenen Ions erhöhen. Viele hingegen ziehen es vor, die NSI als einen Prozess zu definieren, bei dem zwei Elektronen nahezu gleichzeitig ionisiert werden. Diese Definition impliziert, dass neben dem sequentiellen Kanal A + L – > A + + L – > A + + {\displaystyle A+L->A^{+}+L->A^{++}}

Es gibt einen weiteren Kanal A + L – > A + + {\displaystyle A+L->A^{++}}

, die den Hauptbeitrag zur Produktion von doppelt geladenen Ionen bei niedrigeren Intensitäten darstellt. Die erste Beobachtung von dreifachem NSI in Argon, das mit einem 1 µm-Laser wechselwirkt, wurde von Augst et al. berichtet. Später, bei der systematischen Untersuchung des NSI aller Edelgasatome, wurde das vierfache NSI von Xe beobachtet. Die wichtigste Schlussfolgerung dieser Studie war die Beobachtung der folgenden Beziehung zwischen der Rate der NSV zu jedem Ladungszustand und der Rate der Tunnelionisation (vorhergesagt durch die ADK-Formel) zu den vorherigen Ladungszuständen; W N S ( A n + ) = ∑ i = 1 n – 1 α n ( λ ) W A D K ( A i + ) {\displaystyle W_{NS}(A^{n+})=\sum _{i=1}^{n-1}\alpha _{n}\left(\lambda \right)W_{ADK}\left(A^{i+}\right)}

wobei W A D K ( A i + ) {\displaystyle W_{ADK}\left(A^{i+}\right)}

die Rate des quasi-statischen Tunnelns zum i-ten Ladungszustand ist und α n ( λ ) {\displaystyle \alpha _{n}(\lambda )}

sind einige Konstanten, die von der Wellenlänge des Lasers (aber nicht von der Pulsdauer) abhängen.
Zwei Modelle wurden vorgeschlagen, um die nicht-sequenzielle Ionisierung zu erklären; das Shake-off-Modell und das Modell der Elektronenrückstreuung. Das Shake-off (SO)-Modell, das zuerst von Fittinghoff et al. vorgeschlagen wurde, stammt aus dem Bereich der Ionisation von Atomen durch Röntgenstrahlen und Elektronenprojektile, wo der SO-Prozess einer der Hauptmechanismen ist, der für die Mehrfachionisation von Atomen verantwortlich ist. Das SO-Modell beschreibt den NS-Prozess als einen Mechanismus, bei dem ein Elektron durch das Laserfeld ionisiert wird und der Abgang dieses Elektrons so schnell erfolgt, dass die verbleibenden Elektronen nicht genügend Zeit haben, sich auf die neuen Energiezustände einzustellen. Es besteht also eine gewisse Wahrscheinlichkeit, dass nach der Ionisierung des ersten Elektrons ein zweites Elektron zu Zuständen mit höherer Energie angeregt (Shake-up) oder sogar ionisiert (Shake-off) wird. Zu erwähnen ist, dass es bisher keine quantitative Berechnung auf Basis des SO-Modells gibt und das Modell noch qualitativ ist.
Das Elektronenrückstreumodell wurde unabhängig voneinander von Kuchiev, Schafer et al, Corkum, Becker und Faisal sowie Faisal und Becker entwickelt. Die Grundzüge des Modells lassen sich anhand der Version von Corkum leicht nachvollziehen. Das Modell von Corkum beschreibt die NS-Ionisation als einen Prozess, bei dem ein Elektron durch einen Tunnel ionisiert wird. Das Elektron tritt dann in Wechselwirkung mit dem Laserfeld, wo es vom Kern weg beschleunigt wird. Wenn das Elektron in einer geeigneten Phase des Feldes ionisiert wurde, wird es einen halben Zyklus später an der Position des verbleibenden Ions vorbeiziehen, wo es durch Elektronenstoß ein weiteres Elektron freisetzen kann. Nur die Hälfte der Zeit wird das Elektron mit der passenden Phase freigesetzt und die andere Hälfte kehrt es nie zum Kern zurück. Die maximale kinetische Energie, die das zurückkehrende Elektron haben kann, ist das 3,17-fache des ponderomotorischen Potentials ( U p {\displaystyle U_{p}}

) des Lasers. Das Modell von Corkum setzt eine Abschneidegrenze für die minimale Intensität ( U p {\displaystyle U_{p}}

ist proportional zur Intensität), bei der Ionisation aufgrund von Rückstreuung auftreten kann.
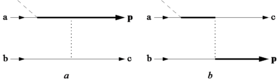
Das Rückstreuungsmodell in der Version von Kuchiev (Kuchievs Modell) ist quantenmechanisch. Die Grundidee des Modells wird durch Feynman-Diagramme in Abbildung a veranschaulicht. Zunächst befinden sich beide Elektronen im Grundzustand eines Atoms. Die mit a und b bezeichneten Linien beschreiben die entsprechenden Atomzustände. Dann wird das Elektron a ionisiert. Der Beginn des Ionisationsprozesses ist durch den Schnittpunkt mit einer schrägen gestrichelten Linie dargestellt. wo der MPI stattfindet. Die Ausbreitung des ionisierten Elektrons im Laserfeld, bei der es weitere Photonen absorbiert (ATI), ist durch die volle dicke Linie dargestellt. Die Kollision dieses Elektrons mit dem Mutter-Atom-Ion ist durch eine vertikale gepunktete Linie dargestellt, die die Coulomb-Wechselwirkung zwischen den Elektronen repräsentiert. Der mit c markierte Zustand beschreibt die Anregung des Ions zu einem diskreten oder Kontinuumszustand. Abbildung b beschreibt den Austauschprozess. Kuchievs Modell sagt im Gegensatz zu Corkums Modell keine Schwellenintensität für das Auftreten der NS-Ionisation voraus.
Kuciev hat die Coulomb-Effekte auf die Dynamik des ionisierten Elektrons nicht berücksichtigt. Dies führte dazu, dass die doppelte Ionisationsrate um einen großen Faktor unterschätzt wurde. Bei dem Ansatz von Becker und Faisal (der im Geiste dem Modell von Kuchiev entspricht) gibt es diesen Nachteil offensichtlich nicht. In der Tat ist ihr Modell genauer und leidet nicht unter der großen Anzahl von Näherungen, die Kuchiev gemacht hat. Ihre Berechnungsergebnisse passen perfekt zu den experimentellen Ergebnissen von Walker et al. Becker und Faisal konnten mit ihrem Modell die experimentellen Ergebnisse zur mehrfachen NSI von Edelgasatomen anpassen. Als Ergebnis kann die Elektronenrückstreuung als Hauptmechanismus für das Auftreten des NSI-Prozesses angenommen werden.
Mehrphotonen-Ionisation innerer Valenzelektronen und Fragmentierung polyatomarer MoleküleBearbeiten
Die Ionisation innerer Valenzelektronen ist verantwortlich für die Fragmentierung polyatomarer Moleküle in starken Laserfeldern. Nach einem qualitativen Modell erfolgt die Dissoziation der Moleküle durch einen dreistufigen Mechanismus:
- MPI von Elektronen aus den inneren Orbitalen des Moleküls, was zu einem Molekül-Ion in ro-Schwingungsniveaus eines angeregten elektronischen Zustands führt;
- schneller strahlungsfreier Übergang zu den hochliegenden ro-Schwingungsniveaus eines niedrigeren elektronischen Zustands; und
- anschließende Dissoziation des Ions zu verschiedenen Fragmenten durch verschiedene Fragmentierungskanäle.







