
Die logistische Regression wurde in den biologischen Wissenschaften im frühen zwanzigsten Jahrhundert verwendet. Sie wurde dann in vielen sozialwissenschaftlichen Anwendungen eingesetzt. Die logistische Regression wird verwendet, wenn die abhängige Variable (Ziel) kategorisch ist.
Zum Beispiel:
- Um vorherzusagen, ob eine E-Mail Spam ist (1) oder (0)
- Ob der Tumor bösartig ist (1) oder nicht (0)
Betrachten Sie ein Szenario, in dem wir klassifizieren müssen, ob eine E-Mail Spam ist oder nicht. Wenn wir für dieses Problem eine lineare Regression verwenden, muss ein Schwellenwert festgelegt werden, anhand dessen die Klassifizierung vorgenommen werden kann. Wenn z. B. die tatsächliche Klasse bösartig ist, der vorhergesagte kontinuierliche Wert 0,4 und der Schwellenwert 0,5 beträgt, wird der Datenpunkt als nicht bösartig klassifiziert, was in Echtzeit zu schwerwiegenden Konsequenzen führen kann.
Aus diesem Beispiel lässt sich ableiten, dass die lineare Regression für das Klassifizierungsproblem nicht geeignet ist. Die lineare Regression ist unbegrenzt, und das bringt die logistische Regression ins Spiel. Ihr Wert liegt streng im Bereich von 0 bis 1.
Einfache logistische Regression
(Vollständiger Quellcode: https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb)
Modell
Ausgang = 0 oder 1
Hypothese => Z = WX + B
hΘ(x) = sigmoid (Z)
Sigmoid Funktion

Wenn ‚Z‘ gegen unendlich geht, wird Y(vorhergesagt) zu 1 und wenn ‚Z‘ gegen negativ unendlich geht, wird Y(vorhergesagt) zu 0.
Analyse der Hypothese
Die Ausgabe der Hypothese ist die geschätzte Wahrscheinlichkeit. Diese wird verwendet, um abzuleiten, wie sicher der vorhergesagte Wert der tatsächliche Wert sein kann, wenn eine Eingabe X gegeben ist. Betrachten Sie das folgende Beispiel,
X = =
Basierend auf dem Wert x1, sagen wir, dass die geschätzte Wahrscheinlichkeit 0,8 ist. Dies besagt, dass die Wahrscheinlichkeit, dass es sich bei einer E-Mail um Spam handelt, bei 80 % liegt.
Mathematisch kann dies wie folgt geschrieben werden,

Dies rechtfertigt den Namen „logistische Regression“. Die Daten werden in ein lineares Regressionsmodell eingepasst, auf das dann eine logistische Funktion einwirkt, die die kategoriale abhängige Zielvariable vorhersagt.
Typen der logistischen Regression
1. Binäre logistische Regression
Die kategoriale Antwort hat nur zwei mögliche Ausgänge. Beispiel: Spam oder nicht
2. Multinomiale logistische Regression
Drei oder mehr Kategorien ohne Ordnung. Beispiel: Vorhersage, welches Lebensmittel mehr bevorzugt wird (Veg, Non-Veg, Vegan)
3. Ordinale logistische Regression
Drei oder mehr Kategorien mit Ordnung. Beispiel: Filmbewertung von 1 bis 5
Entscheidungsgrenze
Um vorherzusagen, zu welcher Klasse die Daten gehören, kann ein Schwellenwert gesetzt werden. Basierend auf diesem Schwellenwert wird die erhaltene geschätzte Wahrscheinlichkeit in Klassen eingeteilt.
Sagen wir, wenn vorhergesagter_Wert ≥ 0,5, dann klassifiziere die E-Mail als Spam, sonst als nicht Spam.
Die Entscheidungsgrenze kann linear oder nicht-linear sein. Die Polynomordnung kann erhöht werden, um komplexe Entscheidungsgrenzen zu erhalten.
Kostenfunktion
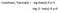
Warum kann die Kostenfunktion, die für die lineare verwendet wurde, nicht für die logistische verwendet werden?
Die lineare Regression verwendet den mittleren quadratischen Fehler als Kostenfunktion. Wenn dies für die logistische Regression verwendet wird, dann ist es eine nicht-konvexe Funktion der Parameter (Theta). Der Gradientenabstieg konvergiert nur dann zum globalen Minimum, wenn die Funktion konvex ist.

Kostenfunktionserläuterung


Vereinfachte Kostenfunktion

Warum diese Kostenfunktion?
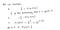
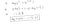
Diese negative Funktion kommt daher, dass wir beim Training die Wahrscheinlichkeit maximieren müssen, indem wir die Verlustfunktion minimieren. Eine Verringerung der Kosten erhöht die maximale Wahrscheinlichkeit unter der Annahme, dass die Stichproben aus einer identisch unabhängigen Verteilung gezogen werden.
Ableiten der Formel für den Gradientenabstiegsalgorithmus


Python-Implementierung
def weightInitialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w,bdef sigmoid_activation(result):
final_result = 1/(1+np.exp(-result))
return final_result
def model_optimize(w, b, X, Y):
m = X.shape
#Prediction
final_result = sigmoid_activation(np.dot(w,X.T)+b)
Y_T = Y.T
cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result)))))
#
#Gradient calculation
dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T))
db = (1/m)*(np.sum(final_result-Y.T))
grads = {"dw": dw, "db": db}
return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations):
costs =
for i in range(no_iterations):
#
grads, cost = model_optimize(w,b,X,Y)
#
dw = grads
db = grads
#weight update
w = w - (learning_rate * (dw.T))
b = b - (learning_rate * db)
#
if (i % 100 == 0):
costs.append(cost)
#print("Cost after %i iteration is %f" %(i, cost))
#final parameters
coeff = {"w": w, "b": b}
gradient = {"dw": dw, "db": db}
return coeff, gradient, costsdef predict(final_pred, m):
y_pred = np.zeros((1,m))
for i in range(final_pred.shape):
if final_pred > 0.5:
y_pred = 1
return y_pred
Kosten vs. Anzahl_der_Iterationen

Die Trainings- und Testgenauigkeit des Systems beträgt 100 %
Diese Implementierung ist für binäre logistische Regression. Für Daten mit mehr als 2 Klassen muss die Softmax-Regression verwendet werden.
Dies ist ein Lehrbeitrag und inspiriert vom Deep-Learning-Kurs von Prof. Andrew Ng.
Voller Code : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb