
In einem früheren Artikel haben wir die lineare Regressionsanalyse und ihre Anwendung in der Finanzanalyse und -modellierung untersucht. Sie können unseren Artikel Regressionsanalyse in der Finanzmodellierung lesen, um mehr über die statistischen Konzepte zu erfahren, die in der Methode verwendet werden und wo sie in der Finanzwelt Anwendung findet.
In diesem Artikel werden wir einen praktischen Blick auf die Modellierung eines multiplen Regressionsmodells für das Bruttoinlandsprodukt (BIP) eines Landes werfen.
Bevor ich beginne, lassen Sie mich einen kurzen Disclaimer hinzufügen. Ich bin kein Statistiker, und ich behaupte nicht, dass die gewählten abhängigen und unabhängigen Variablen die richtige Wahl für die Analyse sind. Ziel dieses Artikels ist es, Ihnen zu zeigen, wie man eine multiple Regression in Excel durchführt und die Ergebnisse interpretiert, und nicht, Sie über die Aufstellung unserer Modellannahmen und die Auswahl der am besten geeigneten Variablen zu unterrichten.
Nun, da wir dies aus dem Weg geräumt haben und die Erwartungen festgelegt sind, lassen Sie uns Excel öffnen und loslegen!
Wir werden für diese Übung öffentliche Daten von Eurostat, der Statistikdatenbank der Europäischen Kommission, beziehen. Alle relevanten Quelldaten befinden sich zu Ihrer Bequemlichkeit in der Modelldatei, die Sie unten herunterladen können. Ich habe auch die Links zu den Quelltabellen beibehalten, um weiter zu erforschen, wenn Sie möchten.
Der EU-Datensatz gibt uns Informationen für alle Mitgliedsstaaten der Union. Als großer Fan von Agatha Christies Hercule Poirot wollen wir unsere Aufmerksamkeit auf Belgien richten.
Wie Sie in der Tabelle unten sehen können, haben wir neunzehn Beobachtungen unserer Zielvariablen (BIP) sowie unsere drei Prädiktorvariablen:
- X1 – Bildungsausgaben in Mio.
- X2 – Arbeitslosenquote in % der Erwerbsbevölkerung;
- X3 – Arbeitnehmerentgelt in Mio.

Selbst bevor wir unser Regressionsmodell ausführen, stellen wir einige Abhängigkeiten in unseren Daten fest. Wenn wir die Entwicklung über die Perioden betrachten, können wir davon ausgehen, dass das BIP zusammen mit den Bildungsausgaben und dem Arbeitnehmerentgelt steigt.
Ausführen einer multiplen linearen Regression
Es gibt Möglichkeiten, alle relevanten Statistiken in Excel mit Formeln zu berechnen. Aber es ist viel einfacher mit dem Datenanalyse-Tool-Pack, das Sie auf der Registerkarte Entwickler -> Excel-Add-ins aktivieren können.
Schauen Sie auf die Registerkarte Daten, und auf der rechten Seite sehen Sie das Datenanalyse-Tool im Abschnitt Analysieren.
Starten Sie es und wählen Sie Regression aus allen Optionen. Beachten Sie, dass wir dasselbe Menü sowohl für einfache (einfache) als auch für multiple lineare Regressionsmodelle verwenden.
Nun ist es an der Zeit, einige Bereiche und Einstellungen festzulegen.
Der Y-Bereich wird unsere abhängige Variable, das BIP, enthalten. Und im X-Bereich werden wir alle Spalten der X-Variablen auswählen. Bitte beachten Sie, dass dies das Gleiche ist wie bei einer einzelnen linearen Regression, der einzige Unterschied ist, dass wir mehrere Spalten für den X-Bereich auswählen.
Erinnern Sie sich daran, dass Excel verlangt, dass alle X-Variablen in benachbarten Spalten sind.
Da ich die Spalte Titel ausgewählt habe, ist es entscheidend, das Kontrollkästchen für Beschriftungen zu markieren. Ein Konfidenzintervall von 95 % ist in den meisten Finanzanalyseszenarien angemessen, daher werden wir dies nicht ändern.
Sie können dann überlegen, ob Sie die Daten auf demselben oder einem neuen Arbeitsblatt platzieren. Ein neues Arbeitsblatt funktioniert in der Regel am besten, da das Tool ziemlich viele Daten einfügt.
Ich werde auch alle zusätzlichen Optionen am unteren Rand markieren. Ich benutze selten alle, aber es ist einfacher, die nicht benötigten zu löschen, als das Ganze noch einmal zu starten.
Melde dich für unseren Newsletter an für eine KOSTENLOSE Excel-Benchmark-Analyse-Vorlage
Auswertung der Regressionsergebnisse
Nun, da wir unsere zusammenfassende Ausgabe von Excel haben, können wir unser Regressionsmodell weiter untersuchen.
Die Informationen, die wir aus dem Datenanalyse-Modul von Excel erhalten haben, beginnen mit der Regressionsstatistik.
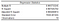
Das R-Quadrat ist das wichtigste davon, also können wir damit beginnen, es zu betrachten. In unserem Fall sollten wir uns insbesondere das bereinigte R-Quadrat ansehen, da wir mehr als eine X-Variable haben. Es gibt uns eine Vorstellung von der Gesamtgüte der Anpassung.
Ein bereinigtes R-Quadrat von 0,98 bedeutet, dass unser Regressionsmodell etwa 98 % der Variation der abhängigen Variable Y (BIP) um den Durchschnittswert der Beobachtungen (den Mittelwert unserer Stichprobe) erklären kann. Mit anderen Worten, 98 % der Variabilität in ŷ (y-hat, unsere abhängige Variable Vorhersagen) wird von unserem Modell erfasst. Ein solch hoher Wert würde normalerweise darauf hinweisen, dass es ein Problem mit unserem Modell geben könnte. Wir werden mit unserem Modell fortfahren, aber ein zu hohes R-Quadrat kann in einem realen Szenario problematisch sein. Ich schlage vor, Sie lesen diesen Artikel auf Statistics by Jim, um zu erfahren, warum zu gut nicht immer richtig ist in Bezug auf R-Quadrat.
Der Standardfehler gibt uns eine Schätzung der Standardabweichung des Fehlers (Residuen). Im Allgemeinen gilt: Wenn der Koeffizient im Vergleich zum Standardfehler groß ist, ist er wahrscheinlich statistisch signifikant.
Varianzanalyse (ANOVA)

Der Abschnitt Varianzanalyse ist etwas, das wir bei der Regressionsmodellierung oft überspringen. Er kann jedoch wertvolle Erkenntnisse liefern und ist es wert, einen Blick darauf zu werfen. Sie können mehr über die Durchführung eines ANOVA-Tests lesen und ein Beispielmodell in unserem entsprechenden Artikel sehen.
Diese Tabelle gibt uns einen allgemeinen Signifikanztest für die Regressionsparameter.
Die F-Spalte der ANOVA-Tabelle gibt uns den allgemeinen F-Test für die Nullhypothese, dass alle Koeffizienten gleich Null sind. Die Alternativhypothese ist, dass mindestens einer der Koeffizienten ungleich Null ist. Die Spalte Signifikanz F zeigt uns den p-Wert für den F-Test an. Da er kleiner als das Signifikanzniveau von 0,05 ist (bei unserem gewählten Konfidenzniveau von 95%), können wir die Nullhypothese, dass alle Koeffizienten gleich Null sind, verwerfen. Das bedeutet, dass unsere Regressionsparameter gemeinsam nicht statistisch insignifikant sind.
Mehr zum Thema Hypothesentests können Sie in unserem entsprechenden Artikel lesen.
Die nächste Tabelle gibt uns Auskunft über die Koeffizienten in unserem multiplen Regressionsmodell und ist der spannendste Teil der Analyse.

Hier haben wir viele Details für den Intercept und jeden unserer Prädiktoren (unabhängige Variablen). Lassen Sie uns untersuchen, was diese Spalten darstellen:
- Koeffizienten – dies sind Schätzungen, die durch die Methode der kleinsten Quadrate abgeleitet wurden;
- Standardfehler – die Standardabweichung der Schätzungen der kleinsten Quadrate;
- T-Stat – dies ist die t-Statistik für die Nullhypothese, dass der Koeffizient gleich Null ist, gegenüber der Alternativhypothese, dass er von Null verschieden ist;
- der P-Wert für den t-Test;
- Untere und obere 95% definieren das Konfidenzintervall für die Koeffizienten.
Test der statistischen Signifikanz
Dies ist der Test der Nullhypothese, die besagt, dass der Koeffizient eine Steigung von Null hat. Wir können uns die p-Werte für jeden Koeffizienten ansehen und sie mit dem Signifikanzniveau von 0,05 vergleichen.
Wenn unser p-Wert kleiner als das Signifikanzniveau ist, bedeutet dies, dass unsere unabhängige Variable statistisch signifikant für das Modell ist. Wenn wir unsere Prädiktoren X1 bis X3 betrachten, stellen wir fest, dass nur X3 Mitarbeitervergütung einen p-Wert von unter 0,05 hat, was bedeutet, dass X1 Bildungsausgaben und X2 Arbeitslosenquote für unser Regressionsmodell nicht statistisch signifikant zu sein scheinen.
Da wir die Nullhypothese (dass die Koeffizienten gleich Null sind) nicht zurückweisen können, können wir X1 und X2 aus dem Modell eliminieren. Wir können dies auch bestätigen, da der Wert Null zwischen der unteren und oberen Konfidenzspanne liegt.
Wir können uns entscheiden, das Modell ohne die Variablen X1 und X2 auszuführen und bewerten, ob dies zu einem signifikanten Rückgang des bereinigten R-Quadrat-Maßes führt. Wenn dies nicht der Fall ist, können wir X1 und X2 aus dem Regressionsmodell entfernen.
Wenn wir das tun, erhalten wir die folgende Regressionsstatistik.

Wir können keinen Abfall des R-Quadrats sehen, also können wir X1 und X2 sicher aus unserem Modell entfernen und es zu einer einzigen linearen Regression vereinfachen.
Residuen-Ausgabe
Die Residuen geben Auskunft darüber, wie weit die tatsächlichen Datenpunkte (y) von den vorhergesagten Datenpunkten (ŷ), basierend auf unserem Regressionsmodell, abweichen.

Wahrscheinlichkeitsausgabe
Diese Tabelle zeigt die beobachteten Werte für die unabhängige Variable (y) und die entsprechenden Perzentile der Stichprobe. Wir können das erste Perzentil als (100 / 2 * Anzahl der Beobachtungen) berechnen, und von dort aus werden diese als das vorherige Perzentil + (100 / 2) berechnet.

Residuen-Diagramme
Die multiple Regressionsanalyse liefert uns ein Diagramm für jede unabhängige Variable gegen die Residuen. Wir können diese Diagramme verwenden, um zu beurteilen, ob unsere Stichprobendaten den Annahmen für Linearität und Homogenität entsprechen.
Homogenität bedeutet, dass das Diagramm ein zufälliges Muster und eine konstante vertikale Streuung aufweisen sollte.
Linearität erfordert, dass die Residuen einen Mittelwert von Null haben. Wir können dies visuell beobachten, indem wir beurteilen, ob die Punkte ungefähr gleichmäßig unter und über der x-Achse verteilt sind.



Line Fit Plots
Das Modell liefert uns einen Line Fit Plot für jede unabhängige Variable (Prädiktor). Dieser zeigt die vorhergesagten Werte (ŷ) gegenüber den beobachteten Werten (y). Je besser diese übereinstimmen, desto besser sagt unser Modell die abhängige Variable auf Basis der Regressoren voraus.



Normalwahrscheinlichkeitsdiagramm
Das Normalwahrscheinlichkeitsdiagramm hilft uns festzustellen, ob die Daten einer Normalverteilung entsprechen. Wir können eine Trendlinie hinzufügen und auswerten, ob die Datenpunkte einer geraden Linie folgen. In unserem Fall ist dies ziemlich offensichtlich, und wir können die Trendlinie nicht einmal hinzufügen.

Das Beispielmodell in Excel können Sie im Originalartikel herunterladen.
Einschränkungen von Excel
Da Excel keine spezialisierte Statistiksoftware ist, gibt es einige inhärente Einschränkungen beim Ausführen eines Regressionsmodells, derer man sich bewusst sein sollte:
- Spalten für alle Regressoren (unabhängige Variablen) müssen nebeneinander liegen;
- Wir können bis zu 16 Prädiktoren haben (ich kann mich nicht erinnern, wo ich das gelesen habe, also nehmen Sie es mit Vorsicht);
- Die Regressionsanalyse in Excel nimmt an, dass der Fehler unabhängig ist und eine konstante Varianz hat (Homoskedastizität);
- Wenn wir den Weg über die Funktionen gehen, ist es wichtig zu wissen, dass die Excel-Funktionen SLOPE, INTERCEPT und FORECAST nicht für die Multiple Regression funktionieren. Im Gegensatz dazu funktionieren TREND und LINEST genauso wie bei einem einzelnen Regressionsmodell, nehmen aber Werte für mehrere X-Variablen an.
Fazit
Wir begannen mit drei unabhängigen Variablen, führten eine Regressionsanalyse durch und stellten fest, dass zwei Prädiktoren keine statistische Signifikanz für unser Modell haben.
Diese haben wir dann eliminiert, um ein einfaches lineares Regressionsmodell zu erhalten.
Sobald Sie mit Ihrem Modell zufrieden sind, können Sie Ihre Regressionsgleichung aufstellen, wie wir in anderen Artikeln besprochen haben. Mit dieser Gleichung können Sie dann die abhängige Variable für die Zukunft prognostizieren.
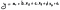
Wo:
- y ist unsere abhängige Variable;
- a ist der Achsenabschnitt (unsere Konstante) aus der Regressionsstatistik;
- b, c und d sind die Koeffizienten für jede Variable;
- x1 bis x3 sind die unabhängigen Variablen (unsere Regressoren oder Prädiktoren);
- ɛ ist der Fehler oder die Residuen, die wir oft ausschließen können.
Denken Sie daran, dass dieser Artikel darauf abzielt, die Konzepte der Durchführung einer multiplen Regressionsanalyse in Excel zu veranschaulichen. Er versucht zu erklären, worauf wir bei der Auswertung der Ergebnisse achten sollten. Jedes gute Modell beginnt mit der Festlegung vernünftiger Annahmen und Erwartungen, in denen ich kein Experte bin, daher erhebe ich keinen Anspruch darauf, dass die gewählten abhängigen und unabhängigen Variablen die richtige Wahl waren.
Danke fürs Lesen! Sie können Ihre Unterstützung zeigen, indem Sie diesen Artikel mit Kollegen und Freunden teilen.