Mechanik der Werkstoffe
Scherspannungsgleichungen und Anwendungen
Allgemeine Scherspannung:
Die Formel zur Berechnung der mittleren Scherspannung lautet:
wobei τ = die Schubspannung; F = die aufgebrachte Kraft; A = die Querschnittsfläche des Materials mit der Fläche senkrecht zum aufgebrachten Kraftvektor;
Trägerschub:
Trägerschub ist definiert als die innere Schubspannung eines Trägers, die durch die auf den Träger aufgebrachte Scherkraft verursacht wird.
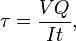mit V = Gesamtschubkraft an der betreffenden Stelle; Q = statisches Flächenmoment; t = Dicke im Material senkrecht zur Schubrichtung; I = Trägheitsmoment der gesamten Querschnittsfläche. Diese Formel ist auch als Jourawski-Formel bekannt.Semi-monocoque shearShear stresses within a semi-monocoque structure may be calculated by idealizing the cross-section of the structure into a set of stringers (carrying only axial loads) and webs (carrying only shear flows). Dividiert man den Scherfluss durch die Dicke eines bestimmten Abschnitts der Halbschalenstruktur, erhält man die Schubspannung. Somit tritt die maximale Schubspannung entweder im Steg des maximalen Scherflusses oder der minimalen Dicke auf.Auch Konstruktionen im Erdreich können durch Scherung versagen; z.B, das Gewicht eines erdgefüllten Dammes oder Deiches kann den Untergrund zum Einsturz bringen, wie ein kleiner Erdrutsch.SchlagscherungDie maximale Scherspannung, die in einem massiven Rundstab bei Schlagbeanspruchung entsteht, ergibt sich aus der Gleichung:
wobei U = Änderung der kinetischen Energie; G = Schermodul; V = Volumen des Stabes; und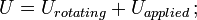 
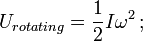
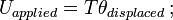
= Massenträgheitsmoment; ω = Winkelgeschwindigkeit.
Schubspannung in Fluiden:
Jedes reale Fluid (Flüssigkeiten und Gase eingeschlossen), das sich entlang einer festen Grenze bewegt, erzeugt eine Schubspannung an dieser Grenze. Die Schlupfbedingung besagt, dass die Geschwindigkeit des Fluids an der Grenze (relativ zur Grenze) Null ist, aber in einer gewissen Höhe von der Grenze muss die Strömungsgeschwindigkeit gleich der des Fluids sein. Der Bereich zwischen diesen beiden Punkten wird treffend als Grenzschicht bezeichnet. Für alle Newtonschen Flüssigkeiten in laminarer Strömung ist die Schubspannung proportional zur Dehnungsrate in der Flüssigkeit, wobei die Viskosität die Proportionalitätskonstante ist. Für nicht Newtonsche Flüssigkeiten ist dies jedoch nicht mehr der Fall, da für diese Flüssigkeiten die Viskosität nicht konstant ist. Die Scherspannung wird durch diesen Geschwindigkeitsverlust auf die Grenzfläche übertragen. Die Schubspannung, für ein Newtonsches Fluid, an einem Flächenelement parallel zu einer ebenen Platte, im Punkt y, ist gegeben durch:
wobei μ die dynamische Viskosität des Fluids, u die Geschwindigkeit des Fluids entlang der Grenzfläche und y die Höhe über der Grenzfläche ist. Im Einzelnen ist die Wandschubspannung definiert als: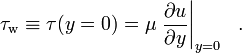 
Im Falle von Wind wird die Schubspannung an der Grenze als Windspannung bezeichnet.
1. Timoshenko, Stephen P. (1983), History of Strength of Material, Courier Dover Publications, S. 141, ISBN 0486611876, http://books.google.com/?id=tkScQmyhsb8C .
2. Day, Michael A. (2004), The no-slip condition of fluid dynamics, Springer Niederlande, S. 285-296, ISSN (Print) 1572-8420 (Online) 0165-0106 (Print) 1572-8420 (Online), http://www.springerlink.com/content/k1m4t1p02m778u88/.
3. Naqwi, A. A.; Reynolds, W. C. (jan 1987), „Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow“, NASA STI/Recon Technical Report N 87
4. Große, S.; Schröder, W. (2009), „Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars“, AIAA Journal 47 (2): 314-321, Bibcode 2009AIAAJ..47..314G, doi:10.2514/1.36892
5. Große, S.; Schröder, W. (2008), „Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³“, International Journal of Heat and Fluid Flow 29 (3): 830-840, doi:10.1016/j.ijheatfluidflow.2008.01.008