- Verhalten des Stichprobenmittelwertes (x-bar)
- Die Stichprobenverteilung des Stichprobenmittelwertes
Verhalten des Stichprobenmittelwerts (x-bar)
Bislang haben wir das Verhalten der Statistik p-hat, den Anteil der Stichprobe, relativ zum Parameter p, dem Anteil der Grundgesamtheit, besprochen (wenn die interessierende Variable kategorisch ist).
Wir gehen nun dazu über, das Verhalten der Statistik x-bar, des Stichprobenmittelwerts, in Bezug auf den Parameter μ (mu), den Populationsmittelwert (wenn die interessierende Variable quantitativ ist), zu untersuchen.
Lassen Sie uns mit einem Beispiel beginnen.
BEISPIEL 9: Verhalten von Stichprobenmittelwerten
Geburtsgewichte werden für alle Babys in einer Stadt erfasst. Das mittlere Geburtsgewicht beträgt 3.500 Gramm, µ = mu = 3.500 g. Wenn wir viele Zufallsstichproben von jeweils 9 Babys sammeln, wie werden sich dann die Stichprobenmittelwerte verhalten?
Auch hier arbeiten wir mit einer Zufallsvariablen, da Zufallsstichproben Mittelwerte haben, die kurzfristig unvorhersehbar variieren, langfristig aber Muster aufweisen.
Basierend auf unserer Intuition und dem, was wir über das Verhalten von Stichprobenproportionen gelernt haben, könnten wir das Folgende über die Verteilung der Stichprobenmittelwerte erwarten:
Mitte: Einige Stichprobenmittelwerte werden auf der niedrigen Seite liegen – sagen wir 3.000 Gramm oder so – während andere auf der hohen Seite liegen werden – sagen wir 4.000 Gramm oder so. Bei wiederholten Stichproben könnte man erwarten, dass sich die Stichproben auf den zugrundeliegenden Populationsmittelwert von 3.500 g mitteln. Mit anderen Worten: Der Mittelwert der Stichprobenmittelwerte wird µ (mu) sein, so wie der Mittelwert der Stichprobenanteile p war.
Streuung: Bei großen Stichproben kann man erwarten, dass die Stichprobenmittelwerte nicht zu weit vom Populationsmittelwert von 3.500 abweichen. Stichprobenmittelwerte, die niedriger als 3.000 oder höher als 4.000 sind, könnten überraschend sein. Bei kleineren Stichproben würden wir weniger von Stichprobenmittelwerten überrascht sein, die ziemlich weit von 3.500 abweichen. Mit anderen Worten, wir würden eine größere Variabilität der Stichprobenmittelwerte für kleinere Stichproben erwarten. Die Stichprobengröße wird also wieder eine Rolle bei der Streuung der Verteilung der Stichprobenmittelwerte spielen, so wie wir es bei den Stichprobenanteilen beobachtet haben.
Shape: Stichprobenmittelwerte, die am nächsten an 3.500 liegen, werden am häufigsten vorkommen, während Stichprobenmittelwerte, die weit von 3.500 entfernt sind, in beiden Richtungen immer unwahrscheinlicher werden. Mit anderen Worten: Die Form der Verteilung der Stichprobenmittelwerte sollte sich in der Mitte ausbeulen und zu den Enden hin verjüngen, mit einer Form, die einigermaßen normal ist. Das ist wiederum das, was wir gesehen haben, als wir uns die Stichprobenanteile angesehen haben.
Kommentar:
- Die Verteilung der Werte des Stichprobenmittelwerts (x-bar) bei wiederholten Stichproben wird als Stichprobenverteilung von x-bar bezeichnet.
Lassen Sie uns eine Simulation betrachten:
Die Ergebnisse, die wir in unseren Simulationen gefunden haben, sind nicht überraschend. Die fortgeschrittene Wahrscheinlichkeitstheorie bestätigt das, indem sie Folgendes behauptet:
Die Stichprobenverteilung des Stichprobenmittelwerts
Wenn wiederholte Zufallsstichproben einer gegebenen Größe n aus einer Grundgesamtheit von Werten für eine quantitative Variable gezogen werden, wobei der Grundgesamtheitsmittelwert μ (mu) und die Grundgesamtheitsstandardabweichung σ (sigma) ist, dann ist der Mittelwert aller Stichprobenmittelwerte (x-Balken) der Grundgesamtheitsmittelwert μ (mu).
Was die Streuung aller Stichprobenmittelwerte betrifft, so gibt die Theorie das Verhalten viel genauer vor, als dass man sagen könnte, dass es bei größeren Stichproben weniger Streuung gibt. Tatsächlich steht die Standardabweichung aller Stichprobenmittelwerte in direktem Zusammenhang mit dem Stichprobenumfang n, wie unten angegeben.
![]()
Da die Quadratwurzel aus dem Stichprobenumfang n im Nenner steht, nimmt die Standardabweichung mit zunehmendem Stichprobenumfang ab.
Lassen Sie uns vergleichen und gegenüberstellen, was wir jetzt über die Stichprobenverteilungen für Stichprobenmittelwerte und Stichprobenanteile wissen.

Nun werden wir die Form der Stichprobenverteilung von Stichprobenmittelwerten untersuchen. Als wir die Stichprobenverteilung von Stichprobenanteilen besprachen, sagten wir, dass diese Verteilung annähernd normal ist, wenn np ≥ 10 und n(1 – p) ≥ 10. Mit anderen Worten, wir hatten eine auf dem Stichprobenumfang basierende Richtlinie zur Bestimmung der Bedingungen, unter denen wir normale Wahrscheinlichkeitsberechnungen für Stichprobenanteile verwenden können.
Wann ist die Verteilung von Stichprobenmittelwerten annähernd normal? Hängt dies von der Größe der Stichprobe ab?
Es scheint einleuchtend, dass eine normalverteilte Population auch bei sehr kleinen Stichproben normalverteilte Stichprobenmittelwerte aufweist. Wir haben dies in der vorherigen Simulation mit Stichproben der Größe 10 gesehen.
Was passiert, wenn die Verteilung der Variablen in der Grundgesamtheit stark schief ist? Haben die Stichprobenmittelwerte auch eine schiefe Verteilung? Wenn wir sehr große Stichproben nehmen, werden die Stichprobenmittelwerte dann normaler verteilt?
In der nächsten Simulation werden wir diese Fragen untersuchen.
Zusammenfassend lässt sich sagen, dass die Verteilung der Stichprobenmittelwerte annähernd normal ist, solange der Stichprobenumfang groß genug ist. Diese Erkenntnis ist wahrscheinlich das wichtigste Ergebnis, das in einführenden Statistikkursen vorgestellt wird. Sie wird formal als Zentraler Grenzwertsatz angegeben.
Wir werden immer wieder auf den Zentralen Grenzwertsatz angewiesen sein, um Normalwahrscheinlichkeitsberechnungen durchzuführen, wenn wir Stichprobenmittelwerte verwenden, um Rückschlüsse auf einen Populationsmittelwert zu ziehen. Wir wissen nun, dass wir dies auch dann tun können, wenn die Grundgesamtheit nicht normalverteilt ist.
Wie groß muss die Stichprobe sein, damit wir annehmen können, dass die Stichprobenmittelwerte normalverteilt sind? Nun, das hängt wirklich von der Populationsverteilung ab, wie wir in der Simulation gesehen haben. Als allgemeine Faustregel gilt, dass Stichproben ab einem Umfang von 30 eine ziemlich normale Verteilung aufweisen, unabhängig von der Form der Verteilung der Variablen in der Grundgesamtheit.
Kommentar:
- Für kategoriale Variablen ist unsere Behauptung, dass Stichprobenproportionen für ausreichend großes n annähernd normal sind, eigentlich ein Spezialfall des zentralen Grenzwertsatzes. In diesem Fall stellen wir uns die Daten als 0er und 1er vor und der „Durchschnitt“ dieser 0er und 1er ist gleich dem besprochenen Anteil.
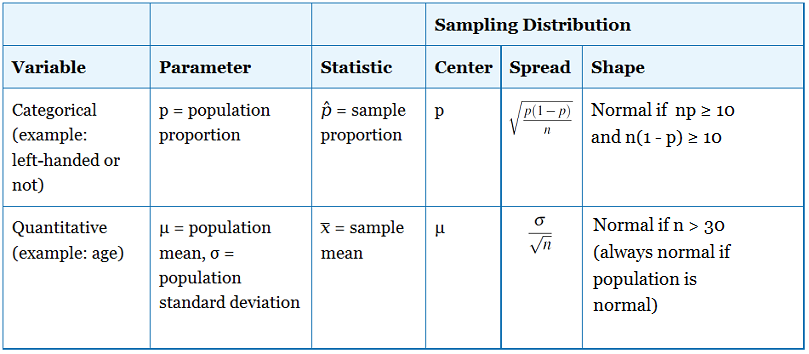
Bevor wir mit einigen Beispielen arbeiten, lassen Sie uns vergleichen und gegenüberstellen, was wir jetzt über die Stichprobenverteilungen für Stichprobenmittelwerte und Stichprobenanteile wissen.
BEISPIEL 10: Verwenden der Stichprobenverteilung von x-bar
Die Haushaltsgröße in den Vereinigten Staaten hat einen Mittelwert von 2,6 Personen und eine Standardabweichung von 1,4 Personen. Es sollte klar sein, dass diese Verteilung rechtsschief ist, da der kleinste mögliche Wert ein Haushalt mit 1 Person ist, die größten Haushalte aber sehr groß sein können.
(a) Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Haushalt mehr als 3 Personen hat?
Eine Normalapproximation sollte hier nicht verwendet werden, da die Verteilung der Haushaltsgrößen stark rechtsschief wäre. Wir haben nicht genug Informationen, um dieses Problem zu lösen.
(b) Wie groß ist die Wahrscheinlichkeit, dass die mittlere Größe einer Zufallsstichprobe von 10 Haushalten größer als 3 ist?
Nach allen Maßstäben ist 10 eine kleine Stichprobengröße. Der zentrale Grenzwertsatz garantiert nicht, dass der Mittelwert einer Stichprobe aus einer schiefen Grundgesamtheit annähernd normal ist, es sei denn, der Stichprobenumfang ist groß.
(c) Wie groß ist die Wahrscheinlichkeit, dass der Mittelwert einer Zufallsstichprobe von 100 Haushalten größer als 3 ist?
Nun können wir uns auf den zentralen Grenzwertsatz berufen: Obwohl die Verteilung der Haushaltsgröße X schief ist, ist die Verteilung der mittleren Haushaltsgröße der Stichprobe (x-bar) für eine große Stichprobengröße wie 100 annähernd normal. Ihr Mittelwert ist derselbe wie der Populationsmittelwert, 2.6, und seine Standardabweichung ist die Standardabweichung der Grundgesamtheit geteilt durch die Quadratwurzel des Stichprobenumfangs:

zu finden
![]()
Wir standardisieren 3 to zu einem z-Score, indem wir den Mittelwert subtrahieren und das Ergebnis durch die Standardabweichung (des Stichprobenmittelwerts) dividieren. Dann können wir die Wahrscheinlichkeit mithilfe des Standard-Normalrechners oder der Tabelle ermitteln.

Haushalte mit mehr als 3 Personen sind natürlich recht häufig, aber es wäre äußerst ungewöhnlich, wenn der Mittelwert einer Stichprobe von 100 Haushalten mehr als 3 betragen würde.
Zweck der nächsten Übung ist es, unter Anleitung die Stichprobenverteilung des Stichprobenmittelwerts (x-bar) zu ermitteln und damit die Wahrscheinlichkeit bestimmter Werte von x-bar kennenzulernen.