Sie fragen sich vielleicht, was es mit all diesen Summen der Quadrate auf sich hat. Vielleicht haben Sie deshalb überhaupt erst hierher gefunden. Nun, sie sind die Determinanten einer guten linearen Regression. Dieses Tutorial basiert auf dem ANOVA-Framework, das Sie vielleicht schon einmal gehört haben.
Bevor Sie es lesen, sollten Sie jedoch sicherstellen, dass Sie Regression nicht mit Korrelation verwechseln. Wenn Sie das geklärt haben, können wir direkt loslegen.
Eine kurze Randnotiz: Möchten Sie mehr über lineare Regression erfahren? Schauen Sie sich unsere Erklärvideos Das lineare Regressionsmodell. Geometrische Darstellung und Das einfache lineare Regressionsmodell.
SST, SSR, SSE: Definition und Formeln
Es gibt drei Begriffe, die wir definieren müssen. Die Gesamtsumme der Quadrate, die Summe der Regressionsquadrate und die Summe der Fehlerquadrate.

Was ist die SST?
Die Gesamtsumme der Quadrate, bezeichnet als SST, ist die quadrierte Differenz zwischen der beobachteten abhängigen Variable und ihrem Mittelwert. Man kann sich dies als die Streuung der beobachteten Variablen um den Mittelwert vorstellen – ähnlich wie die Varianz in der deskriptiven Statistik.
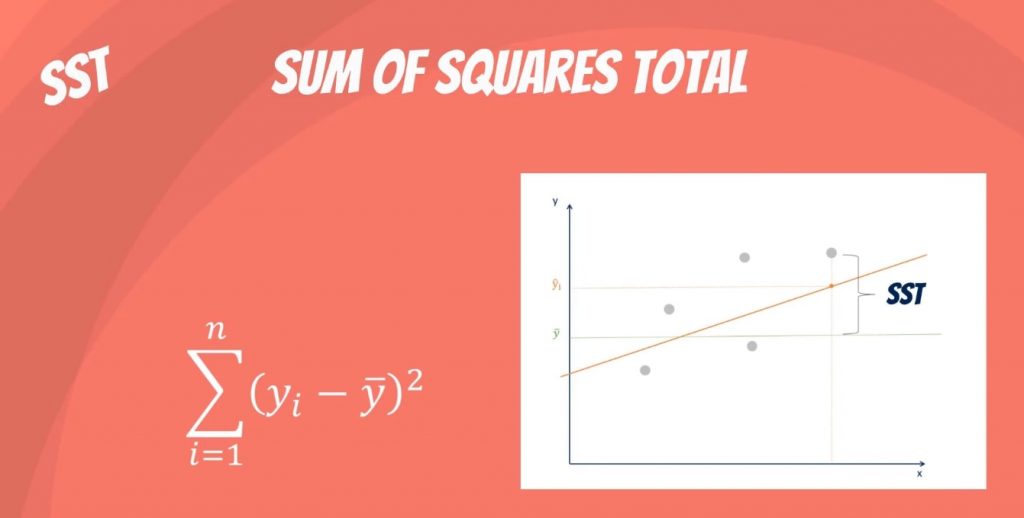
Es ist ein Maß für die Gesamtvariabilität des Datensatzes.
Nebenbei bemerkt: Es gibt eine weitere Schreibweise für die SST. Sie lautet TSS oder Gesamtsumme der Quadrate.
Was ist die SSR?
Der zweite Term ist die Summe der Quadrate aufgrund der Regression, oder SSR. Es ist die Summe der Differenzen zwischen dem vorhergesagten Wert und dem Mittelwert der abhängigen Variable. Betrachten Sie es als ein Maß, das beschreibt, wie gut unsere Linie zu den Daten passt.

Wenn dieser Wert der SSR gleich der Summe der Quadrate ist, bedeutet das, dass unser Regressionsmodell die gesamte beobachtete Variabilität erfasst und perfekt ist. Noch einmal sei erwähnt, dass eine andere gebräuchliche Schreibweise ESS oder erklärte Summe der Quadrate ist.
Was ist die SSE?
Der letzte Term ist der Fehler der Summe der Quadrate, oder SSE. Der Fehler ist die Differenz zwischen dem beobachteten Wert und dem vorhergesagten Wert.

In der Regel wollen wir den Fehler minimieren. Je kleiner der Fehler ist, desto besser ist die Schätzkraft der Regression. Schließlich sollte ich noch hinzufügen, dass es auch als RSS oder Residualsumme der Quadrate bekannt ist. Residual wie in: verbleibend oder unerklärt.
Die Verwirrung zwischen den verschiedenen Abkürzungen
Es wird wirklich verwirrend, weil manche Leute es als SSR bezeichnen. Dadurch wird unklar, ob es sich um die Summe der Quadrate aufgrund der Regression oder um die Summe der quadrierten Residuen handelt.

In jedem Fall ist keine dieser beiden Bezeichnungen allgemein gebräuchlich, also bleibt die Verwirrung bestehen und wir müssen damit leben.
Erinnern Sie sich einfach daran, dass die beiden Bezeichnungen SST, SSR, SSE oder TSS, ESS, RSS lauten.

Es gibt einen Konflikt bezüglich der Abkürzungen, aber nicht über das Konzept und seine Anwendung. Konzentrieren wir uns also darauf.
Wie hängen sie zusammen?
Mathematisch ist SST = SSR + SSE.

Das Grundprinzip ist folgendes: Die Gesamtvariabilität des Datensatzes ist gleich der durch die Regressionsgerade erklärten Variabilität plus der unerklärten Variabilität, bekannt als Fehler.

Bei einer konstanten Gesamtvariabilität wird ein geringerer Fehler eine bessere Regression bewirken. Umgekehrt wird ein höherer Fehler eine weniger starke Regression bewirken. Und das ist es, was Sie sich merken müssen, egal in welcher Notation.
Nächster Schritt: Das R-Quadrat
Wenn Sie sich nicht sicher sind, wozu wir all diese Quadratsummen brauchen, haben wir genau das richtige Werkzeug für Sie. Das R-Quadrat. Möchten Sie mehr darüber erfahren? Tauchen Sie einfach in das verlinkte Tutorial ein, wo Sie verstehen werden, wie es die Erklärungskraft einer linearen Regression misst!
***
Interessiert, mehr zu lernen? Mit unserem Statistik-Kurs können Sie Ihre Fähigkeiten von gut zu großartig bringen.
Statistikkurs kostenlos testen
Nächstes Tutorial: Variabilität messen mit dem R-Quadrat