Guinguette Marais Poitevin

Objetivos de aprendizaje

Un fenómeno experimental que no podía ser explicado adecuadamente por la física clásica era la radiación del cuerpo negro. Los objetivos de esta sección incluyen

• Familiarizarse con los radiadores de cuerpo negro
• Aplicar la Ley de Stefan-Boltmann para estimar la salida total de luz de un radiador
• Aplicar la Ley de Desplazamiento de Wien para estimar la longitud de onda pico (o frecuencia) de la salida de un radiador de cuerpo negro
• Entender la Ley de Rayleigh-Jeans y cómo no modela adecuadamente la radiación de los cuerpos negros

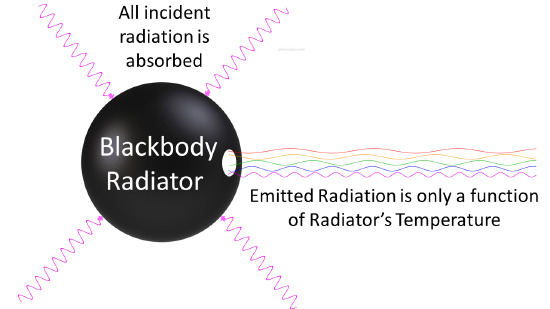
Toda la materia normal a temperaturas superiores al cero absoluto emite radiación electromagnética, que representa una conversión de la energía térmica interna de un cuerpo en energía electromagnética, por lo que se denomina radiación térmica. A la inversa, toda la materia normal absorbe la radiación electromagnética en algún grado. Un objeto que absorbe TODA la radiación que incide sobre él, en todas las longitudes de onda, se denomina cuerpo negro. Cuando un cuerpo negro está a una temperatura uniforme, su emisión tiene una distribución de frecuencia característica que depende de la temperatura. Esta emisión se llama radiación de cuerpo negro.

Un cuerpo negro a temperatura ambiente parece negro, ya que la mayor parte de la energía que irradia es infrarroja y no puede ser percibida por el ojo humano. Dado que el ojo humano no puede percibir las ondas de luz en las frecuencias más bajas, un cuerpo negro, visto en la oscuridad a la temperatura más baja apenas visible, parece subjetivamente gris, aunque su espectro físico objetivo alcanza su punto máximo en el rango infrarrojo. Cuando se calienta un poco más, aparece de color rojo apagado. A medida que aumenta su temperatura, se vuelve amarillo, blanco y, finalmente, blanco-azulado.



La radiación del cuerpo negro tiene un espectro de frecuencias característico y continuo que, experimentalmente, sólo depende de la temperatura del cuerpo. De hecho, podemos ser mucho más precisos:

Un cuerpo emite radiación a una temperatura y frecuencia determinadas exactamente igual que absorbe la misma radiación.

Esta afirmación fue demostrada por Gustav Kirchhoff: el punto esencial es que si en cambio suponemos que un cuerpo particular puede absorber mejor de lo que emite, entonces en una habitación llena de objetos todos a la misma temperatura, absorberá la radiación de los otros cuerpos mejor de lo que irradia energía hacia ellos. Esto significa que se calentará, y el resto de la habitación se enfriará, contradiciendo la segunda ley de la termodinámica. Por lo tanto, un cuerpo debe emitir radiación exactamente igual de bien que absorbe la misma radiación a una temperatura y frecuencia dadas para no violar la segunda ley de la termodinámica.

Cualquier cuerpo a cualquier temperatura por encima del cero absoluto irradiará en cierta medida, la intensidad y la distribución de la frecuencia de la radiación dependen de la estructura detallada del cuerpo. Para empezar a analizar la radiación de calor, tenemos que ser específicos sobre el cuerpo que irradia: el caso más simple posible es un cuerpo idealizado que es un absorbente perfecto, y por lo tanto también (desde el argumento anterior) un emisor perfecto. Entonces, ¿cómo se construye un absorbente perfecto en el laboratorio? En 1859 Kirchhoff tuvo una buena idea: un pequeño agujero en el lateral de una caja grande es un excelente absorbente, ya que cualquier radiación que atraviesa el agujero rebota en su interior, absorbiendo una gran cantidad en cada rebote, y tiene pocas posibilidades de volver a salir. Así que podemos hacer esto a la inversa: tener un horno con un pequeño agujero en el lateral, y presumiblemente la radiación que sale por el agujero es una representación tan buena de un emisor perfecto como la que vamos a encontrar (Figura \(\PageIndex{2}\)).



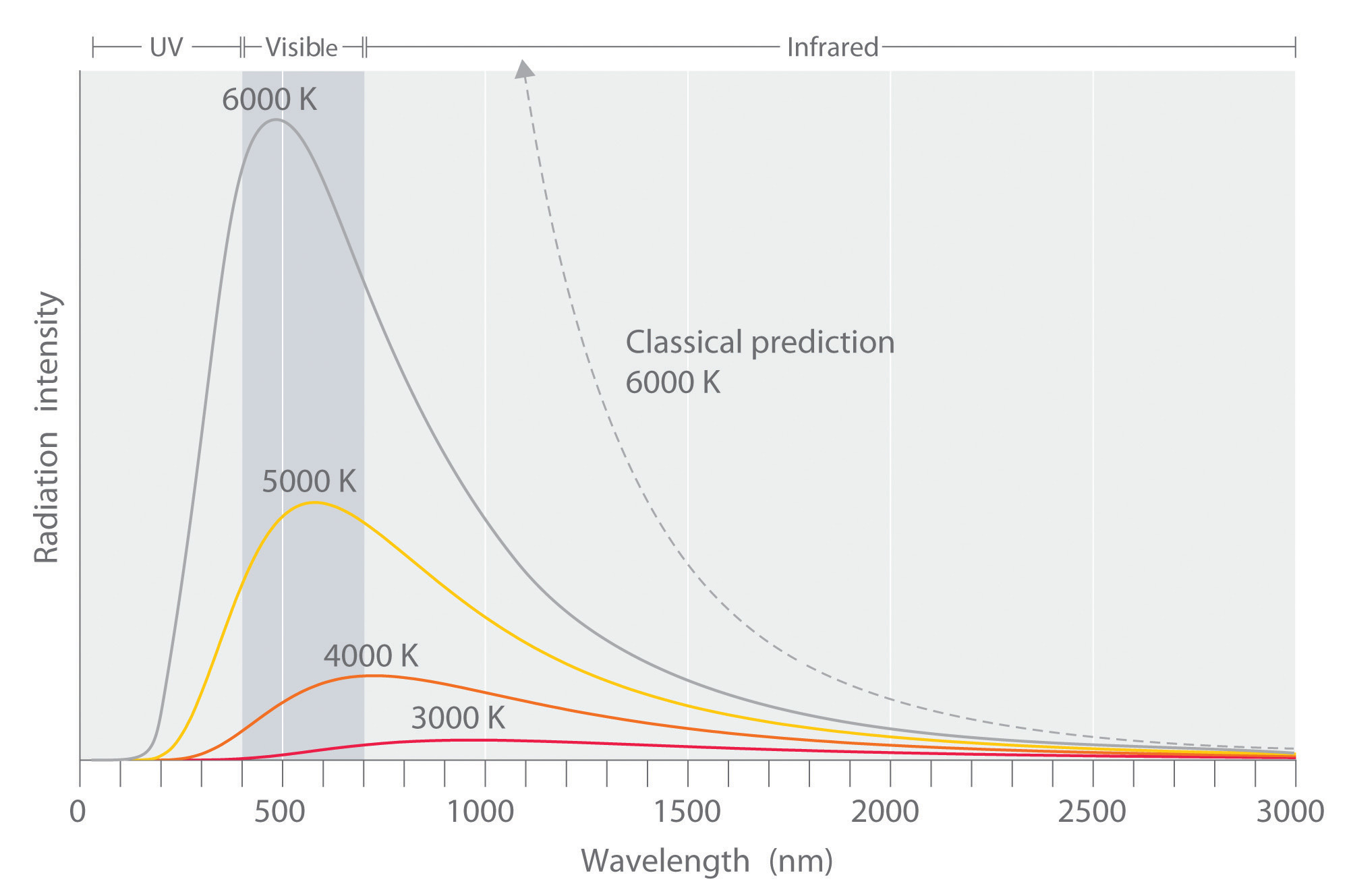
En la década de 1890, las técnicas experimentales habían mejorado lo suficiente como para poder realizar mediciones bastante precisas de la distribución de energía de la radiación del cuerpo negro. En 1895, en la Universidad de Berlín, Wien y Lummer perforaron un pequeño agujero en el lateral de un horno que, por lo demás, estaba completamente cerrado, y comenzaron a medir la radiación que salía. El haz que salía del agujero se hacía pasar por una rejilla de difracción, que enviaba las diferentes longitudes de onda/frecuencias en distintas direcciones, todas ellas hacia una pantalla. Se movió un detector hacia arriba y hacia abajo a lo largo de la pantalla para encontrar cuánta energía radiante se emitía en cada rango de frecuencia. Encontraron una curva de intensidad de radiación/frecuencia cercana a las distribuciones de la Figura \(\PageIndex{3}\).



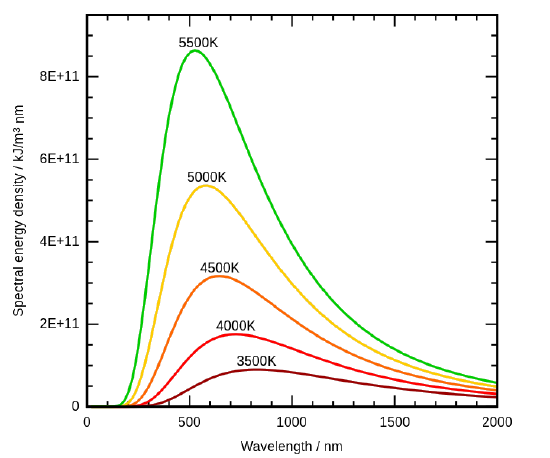
Al medir las curvas de emisión del cuerpo negro a diferentes temperaturas (Figura \(\PageIndex{3}\)), también fueron capaces de construir dos importantes Leyes fenomenológicas (es decir, formuladas a partir de observaciones experimentales, no de principios básicos de la naturaleza): La Ley de Stefan-Boltmann y la Ley de Desplazamiento de Wien.

No todos los radiadores son de cuerpo negro

La radiación de un radiador de cuerpo negro se produce por la actividad térmica del material, no por la naturaleza del mismo, ni por cómo se excitó térmicamente. Algunos ejemplos de cuerpos negros son las bombillas incandescentes, las estrellas y las estufas calientes. La emisión aparece como un espectro continuo (Figura \(\PageIndex{3}\)) con múltiples colores coexistentes. Sin embargo, no todos los radiadores son de cuerpo negro. Por ejemplo, la emisión de una bombilla de fluorescencia no lo es. El siguiente espectro muestra la distribución de la luz de un tubo de luz fluorescente y es una mezcla de bandas discretas a diferentes longitudes de onda de la luz en contraste con los espectros continuos de la Figura \(\PageIndex{3}) para los radiadores de cuerpo negro.



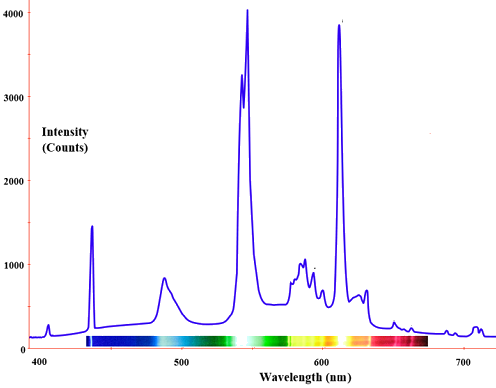
Las bombillas fluorescentes contienen una mezcla de gases inertes (normalmente argón y neón) junto con una gota de mercurio a baja presión. Una mezcla diferente de colores visibles se mezclan para producir una luz que nos parece blanca con diferentes matices.

La Ley de Stefan-Boltzmann

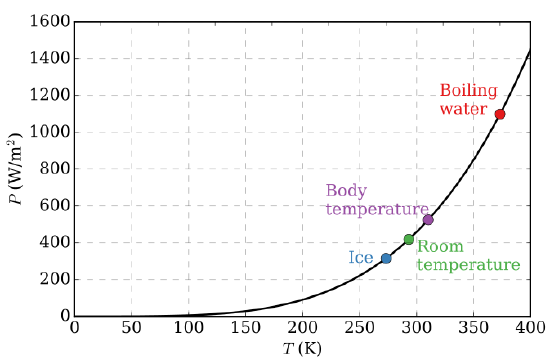
La primera conjetura cuantitativa basada en observaciones experimentales fue la Ley de Stefan-Boltzmann (1879) que establece la potencia total (es decir, integrada sobre todas las frecuencias emisoras en la Figura \(\PageIndex{3}\)) radiada por un metro cuadrado de superficie negra va como la cuarta potencia de la temperatura absoluta (Figura \(\PageIndex{4}\)):

donde

• (P\) es la cantidad total de radiación emitida por un objeto por metro cuadrado (\(Watts\; m^{-2}\))
• (\sigma\) es una constante llamada constante de Stefan-Boltzman (\(5.67 \times 10^{-8}\, Watts\; m^{-2} K^{-4}\))
• (T\) es la temperatura absoluta del objeto (en K)

La Ley de Stefan-Boltzmann se observa fácilmente comparando el valor integrado (es decir, bajo las curvas) de la distribución experimental de la radiación del cuerpo negro en la figura \(\PageIndex{3}) a diferentes temperaturas. En 1884, Boltzmann dedujo este comportamiento \(T^4\) de la teoría aplicando el razonamiento termodinámico clásico a una caja llena de radiación electromagnética, utilizando las ecuaciones de Maxwell para relacionar la presión con la densidad de energía. Es decir, la pequeña cantidad de energía que sale del agujero (Figura \(\PageIndex{2}\)) tendría, por supuesto, la misma dependencia de la temperatura que la intensidad de la radiación en el interior.



Ejemplo \(\PageIndex{1}\)

La temperatura de la superficie del sol es de 5700 K.

1. ¿Cuánta energía irradia el sol?
2. Dado que la distancia a la tierra es de unos 200 radios solares, ¿cuál es la máxima potencia posible de una instalación de energía solar de un kilómetro cuadrado?

Solución

(a) Primero calculamos el área del sol seguido del flujo (potencia). El sol tiene un radio de \( 6,96 \times 10^{8} m \)

El área del sol es \( A = 4 \pi R^{2} \).

&= 6.08 \times 10^{18} m^2 \end{align*}]

La potencia que irradia el sol (mediante la ley de Stefan-Boltzmann) es \(P = \sigma T^{4} \️).

&= 5,98 \times 10^{7} Vatios/m^2 \end{align*}]

Este valor es por metro cuadrado.

(b) Para calcular la potencia total irradiada por el sol es así:

&= 3,6 \c veces 10^{26} Watts \end{align*}]

Ley de desplazamiento de Wien

La segunda observación fenomenológica del experimento fue la Ley de desplazamiento de Wien. La ley de Wien identifica la longitud de onda dominante (pico), o el color, de la luz procedente de un cuerpo a una temperatura determinada. A medida que varía la temperatura del horno, también lo hace la frecuencia a la que la radiación emitida es más intensa (Figura \(\PageIndex{3}\)). De hecho, esa frecuencia es directamente proporcional a la temperatura absoluta:

donde la constante de proporcionalidad es \(5,879 \times 10^{10} Hz/K\).

El propio Wien dedujo esta ley teóricamente en 1893, siguiendo el razonamiento termodinámico de Boltzmann. Anteriormente había sido observada, al menos de forma semicuantitativa, por un astrónomo estadounidense, Langley. Este desplazamiento ascendente de \(\nu_{max}\ con \(T\) es conocido por todos: cuando se calienta un hierro en el fuego (Figura \(\PageIndex{1}\)), la primera radiación visible (a unos 900 K) es de color rojo intenso, la luz visible de más baja frecuencia. Un mayor aumento de \(T\) hace que el color cambie a naranja, luego a amarillo y finalmente a azul a temperaturas muy altas (10.000 K o más) para las que el pico de intensidad de la radiación se ha desplazado más allá del visible hacia el ultravioleta.

Otra representación de la Ley de Wien (Ecuación \ref{Eq2}) en términos de la longitud de onda pico de la luz es

donde \(T\) es la temperatura absoluta en kelvin y \(b\) es una constante de proporcionalidad llamada constante de desplazamiento de Wien, igual a \(2.89 \times 10^{-3} m\, K\), o más convenientemente para obtener la longitud de onda en micrómetros, \(b≈2900\; μm \cdot K\). Se trata de una relación inversa entre la longitud de onda y la temperatura. Así, cuanto más alta es la temperatura, más corta o menor es la longitud de onda de la radiación térmica. Cuanto menor sea la temperatura, mayor será la longitud de onda de la radiación térmica. En el caso de la radiación visible, los objetos calientes emiten una luz más azul que los objetos fríos.

Si la temperatura superficial del cuerpo es de 90 °F.

1. ¿Cuánta energía radiante en \(W\, m^{-2}\) emitiría su cuerpo?
2. ¿Cuál es la longitud de onda máxima de la radiación emitida?
3. ¿Cuál es la energía radiante total emitida por su cuerpo en vatios? Nota: El varón adulto medio tiene una superficie corporal de unos 1,9 \2\️ y la superficie corporal media de una mujer es de unos 1,6 \️.

Solución

(a) 90 °F son 305 K. Utilizamos la Ley de Stefan-Boltzmann (Ecuación \ref{Eq1}. La cantidad total de radiación emitida será \( P = \sigma T^4 \).

&= 491 W\, m^{-2} end{align*}]

La longitud de onda máxima de la radiación emitida se encuentra utilizando la Ley de Wien:

&= \frac{ 2.898 \N veces 10^{-3} m \cdot K}{305 K} &= 9,5 veces 10^{-6} m = 9,5 \mu mend{align*}]

La densidad de energía radiante total en vatios es :

\text{Energía}{{texto}{femenino} &= (491 W\, m^{-2})(1,6 m^{2}) = 786 W \end{align*}]

Ejemplo \(\PageIndex{3}\N:) La temperatura del Sol

Por ejemplo, si el Sol tiene una temperatura superficial de 5700 K, ¿cuál es la longitud de onda de máxima intensidad de la radiación solar?

Solución

Si sustituimos 5700 K por \(T\) en la ecuación \(\ref{Eq2a}\), tenemos

&= 5.1 \Nveces 10^{-7}

Sabiendo que la luz violeta tiene una longitud de onda de unos \(4,0 \times 10^{-7}\) metros, la amarilla de unos \(5,6 \times 10^{-7}\) metros, y la roja de unos \(6,6 \times 10^{-7}\) metros, ¿qué podemos decir sobre el color de la radiación máxima del Sol? La longitud de onda máxima de la radiación solar es ligeramente más corta que el color amarillo, por lo que es un amarillo ligeramente verdoso. Para ver este tinte verdoso del Sol, habría que mirarlo desde el espacio. Resulta que la atmósfera de la Tierra dispersa algunas de las ondas más cortas de la luz solar, lo que desplaza su longitud de onda máxima al amarillo puro.

Recuerde que la radiación térmica siempre abarca una amplia gama de longitudes de onda (Figura \(\PageIndex{2})) y la ecuación \ref{Eq2a} sólo especifica la única longitud de onda que es el pico del espectro. Por tanto, aunque el Sol aparece de color blanco amarillento, cuando se dispersa la luz solar con un prisma se ve la radiación con todos los colores del arco iris. El amarillo sólo representa una longitud de onda característica de la emisión.

Ejercicio (\PageIndex{1})

1. ¿A qué longitud de onda emite el Sol la mayor parte de su radiación si tiene una temperatura de 5.778 K?
2. ¿A qué longitud de onda emite la Tierra la mayor parte de su radiación si tiene una temperatura de 288 K?
Respuesta a

500 nm

Respuesta b

10,0 micras

La ley de Rayleigh-Jeans

Lord Rayleigh y J. H. Jeans desarrollaron una ecuación que explicaba la radiación del cuerpo negro a bajas frecuencias. La ecuación que parecía expresar la radiación del cuerpo negro se basaba en todas las suposiciones conocidas de la física de la época. La gran suposición que implicaban Rayleigh y Jean era que se añadían continuamente cantidades infinitesimales de energía al sistema cuando se aumentaba la frecuencia. La física clásica suponía que la energía emitida por las oscilaciones atómicas podía tener cualquier valor continuo. Esto era cierto para todo lo que se había estudiado hasta ese momento, incluyendo cosas como la aceleración, la posición o la energía. Su Ley de Rayleigh-Jeans resultante fue

&= \dfrac{8 \pi k_B T}{c^3} \nu^2 d\nu \label{Eq3} \end{align}]

Los datos experimentales realizados en la caja negra mostraron resultados ligeramente diferentes a los esperados por la ley de Rayleigh-Jeans (Figura \(\PageIndex{5}\)). La ley había sido estudiada y ampliamente aceptada por muchos físicos de la época, pero los resultados experimentales no mentían, algo era diferente entre lo que se teorizaba y lo que realmente ocurre. Los resultados experimentales mostraban una curva tipo campana, pero según la ley de Rayleigh-Jeans la frecuencia divergía al acercarse a la región ultravioleta (Ecuación \ref{Eq3}\). Ehrenfest lo bautizó posteriormente como la «catástrofe ultravioleta».

Es importante destacar que la ecuación \(\ref{Eq3}\ es un resultado clásico: las únicas entradas son la dinámica clásica y la teoría electromagnética de Maxwell. La carga \(e\) del oscilador no aparece: el resultado es independiente de la fuerza de acoplamiento entre el oscilador y la radiación, el acoplamiento sólo tiene que ser lo suficientemente fuerte para asegurar el equilibrio térmico. La derivación de la ley se puede encontrar aquí.



Representación diferencial frente a integral de la distribución

La radiación se entiende como una distribución continua de amplitud frente a la longitud de onda o, lo que es lo mismo, frente a la frecuencia (Figura \(\PageIndex{5}\)). A una frecuencia específica \(\nu\), según la ley de Rayleigh-Jeans, la radiación es

En la práctica, es difícil medir una sola frecuencia y nos interesan más los intervalos de frecuencia. Una frecuencia exacta es el límite de una secuencia de intervalos cada vez más pequeños. Si hacemos la suposición de que, para un intervalo suficientemente pequeño, \(ρ(\nu,T)\ no varía, obtenemos su definición para la diferencial \(dρ(ν,T)\) en la ecuación \ref{Eq3}:

La suposición es justa debido a la continuidad de \(ρ(\nu,T)\). Se trata de la aproximación de una integral sobre un intervalo muy pequeño \(d\nu\) por la altura de un punto dentro de este intervalo (\(\frac{8\pi k_bT\nu^2}{c^3}\)) por su longitud (\(d\nu\)). Entonces, si sumamos una cantidad infinita de pequeños intervalos como el anterior obtenemos una integral. La radiación total entre \(\nu_1\) y \(\nu_2\) será:

Obsérvese que \(ρ(\nu,T)\) es cuadrática en \(\nu\).

Ejemplo \(\PageIndex{4}\N: la catástrofe del ultravioleta

¿Cuál es la radiancia espectral total de un radiador que sigue la ley de Rayleigh-Jeans para su espectro de emisión?

Solución

La radiancia espectral total \(\rho_{tot}(T)\Nes la emisión combinada sobre todas las posibles longitudes de onda (o equivalentemente, frecuencias), que es una integral sobre la distribución correspondiente (Ecuación \ref{Eq3} para la ley de Rayleigh-Jeans).

&= \int_0^\infty \dfrac{8 \pi k_B T}{c^3} \nu^2 d\nu \nend{align*}]

pero la integral

no converge. Peor aún, es infinita,

Por lo tanto, la ley clásica de Rayleigh-Jeans predice que la radiación de un cuerpo negro es infinita. Dado que la radiación es la potencia por ángulo y unidad de superficie, esto también implica que la potencia total y, por tanto, la energía que emite un cuerpo negro es infinita, lo cual es claramente absurdo. Esto se llama la catástrofe ultravioleta porque la predicción absurda se debe a que la ley clásica no predice correctamente el comportamiento a altas frecuencias/longitudes de onda pequeñas (Figura \(\PageIndex{5}\)).

Contribuidores

• Michael Fowler (Beams Professor, Department of Physics, University of Virginia)

• David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski («Quantum States of Atoms and Molecules»)

• Paul Flowers (University of North Carolina – Pembroke), Klaus Theopold (University of Delaware) y Richard Langley (Stephen F. Austin State University) con autores colaboradores. El contenido del libro de texto producido por OpenStax College se encuentra bajo una licencia Creative Commons Attribution License 4.0. Descárgalo gratuitamente en http://cnx.org/contents/85abf193-2bd…[email protected]).

• ACuriousMind (StackExchange)

Cuidado con los niños.