El método 3-4-5 para escuadrar las esquinas
Por Robert Robillard en Reparaciones y Remodelaciones del Hogar
Método del triángulo 3-4-5
La carpintería no es una ciencia exacta; es un enfoque pragmático para resolver problemas, construir y reparar. Mi experiencia me ha enseñado que unos pocos principios básicos nos guían sobre lo que funcionará o no. Plomada, Nivel y Escuadra son algunos de esos principios.
Regla 3-4-5 Para Asegurar Trazados Cuadrados
Los carpinteros y constructores suelen utilizar el método 3-4-5 para cuadrar las esquinas y asegurarse de que los proyectos que están construyendo tienen un ángulo preciso de 90 grados.
En el mundo residencial y de la construcción los carpinteros suelen utilizar escuadras de velocidad y escuadras de encuadre para comprobar los trazados.
Cuando el trazado es grande estas escuadras de encuadre son simplemente demasiado pequeñas para garantizar la precisión necesaria. Los grandes proyectos de remodelación y construcción, como el trazado de los cimientos de una casa o de las paredes, a menudo emplean una técnica de triángulo 3-4-5 para garantizar ángulos precisos de 90 grados.
Evite los errores de composición
No importa el proyecto en el que trabaje, si la base o los cimientos no están nivelados, a plomo y a escuadra, el resto del proyecto estará mal. Los errores en la base de una cubierta, una casa o un porche seguirán creciendo y agravándose para cuando llegue a los acabados, los armarios o llegue a la estructura del tejado.

3-4-5 Reglas en términos sencillos:
Si el lado corto del triángulo es de 3 pies, y el cateto que se extiende desde él 90 grados es de 4 pies, la hipotenusa, o cateto más largo, será de 5 pies.
Esta técnica simplemente requiere que el carpintero cree un triángulo en la esquina de las líneas que van a ser cuadradas (90 grados) entre sí.
El triángulo 3-4-5 debe tener
- Un lado (cateto del triángulo) que mide 3 pies
- Un segundo lado (cateto del triángulo) que mide 4 pies
- Un tercer lado, que conecta los dos catetos que miden 5 pies
- 3-4-5
- 6-8-10
- 9-12-15
- 12- 16-20
- 15-20-25
- Ajuste de Puertas Deslizantes
- Reemplazo de Ventanas mosquiteras
- Guía de suelos laminados
- Planificación de una remodelación
- Reparación de faroles de cobre
Cualquier triángulo con lados de 3, 4 y 5 pies tendrá un ángulo de 90 grados frente al lado de 5 pies. La belleza y simplicidad de esta técnica es que si el carpintero o constructor necesita aumentar la precisión en paredes o estructuras más grandes, se puede desplegar cualquier múltiplo de la regla 3-4-5.
Ejemplos de la regla 3-4-5
¿Por qué funciona?
Matemáticamente, ¿por qué el método 3-4-5 para cuadrar esquinas crea un ángulo recto perfecto?
En Geometría, un método bien conocido para construir el ángulo recto es emplear el Teorema de Pitágoras. El matemático Pitágoras descubrió una relación entre los lados de cualquier triángulo rectángulo que ahora se conoce como el Teorema de Pitágoras. Pitágoras demostró que el cuadrado del lado más largo (la hipotenusa) es igual a la suma de los cuadrados de los dos lados restantes.
Esto se escribe como la siguiente ecuación:
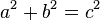
A y B son los dos catetos del triángulo rectángulo y C es la hipotenusa. Si sustituimos los números de un triángulo 3-4-5 en esta fórmula, tenemos entonces 9″ + 16″ = 25″![]()
Recordando el 3-4-5
Utilizar las dimensiones de los triángulos de 3, 4 y 5 es fácil de recordar y desplegar. No hay ecuaciones difíciles de recordar y el método 3-4-5 siempre producirá un ángulo recto perfecto cada vez.
¿Qué pasa si la última medida está apagada?
Cuando se utiliza el método 3-4-5 para cuadrar las esquinas, si su última medida que conecta las dos piernas de medición está apagada y no es cuadrada tendrá que hacer ajustes.
Los ajustes normalmente significan mover un lado, ya sea la pata del triángulo de 3 o 4 pies hacia dentro o hacia fuera para obtener la medida cuadrada de 5 pies.