Esta pregunta es más complicada de lo que crees

¿Cuántas hormigas hacen falta para levantar la Tierra? Esta puede parecer una pregunta muy sencilla. Básicamente, necesitaríamos saber dos cosas: 1, cuánta masa puede levantar una hormiga, y 2, cuánta masa tiene la Tierra. Dividiendo el segundo número entre el primero se obtiene la respuesta deseada. ¿Correcto?
Bueno, en primer lugar, tenemos que decidir dónde vamos a levantar la Tierra en nuestro pequeño experimento mental. Normalmente, cuando hacemos preguntas del tipo «¿Cuánto X se necesita para levantar Y?», nos referimos a «en la Tierra». Para ello tenemos que levantar la Tierra en la Tierra, pero como esto es un experimento mental, no dejemos que eso se interponga. Supongamos que estamos en la Tierra y tenemos una «segunda Tierra», E2, que queremos que nuestras hormigas levanten. Lo único importante de E2 es que tiene la misma masa, forma y tamaño que nuestra Tierra.
E2 tiene un campo gravitatorio igual al de la Tierra.
Muy bien, así que ahora sólo tenemos que dividir la masa de E2 entre la masa que puede levantar una hormiga, como hemos dicho, ¿no? En realidad no. La cuestión es un poco más complicada que esto. Verás, este método funciona para objetos «normales», como un libro, una piedra o incluso un autobús. El E2, sin embargo, es mucho más pesado que esto. Tanto, que tiene un campo gravitatorio igual al de la Tierra (ya que su masa es igual a la de la Tierra). En el caso de los objetos normales que caen, sólo hay que tener en cuenta el campo gravitatorio de la Tierra, no el del objeto, que es efectivamente inexistente. En tal situación, podemos calcular fácilmente la fuerza que ejerce la Tierra sobre un objeto multiplicando la masa en kilogramos del objeto por 9,81 para obtener una fuerza en newtons. E2, sin embargo, es demasiado pesado para esto.
Lo que necesitamos saber es la fuerza que mantiene nuestro hipotético E2 contra la Tierra.
Lo que necesitamos saber es la fuerza que mantiene nuestro hipotético E2 contra la Tierra. Luego podemos calcular cuántas hormigas se necesitan para contrarrestar esta fuerza. La fuerza que mantiene a E2 contra la Tierra se puede calcular con la siguiente fórmula, calculando la fuerza F entre dos masas (ambas denotadas con una m) con una distancia r entre ellas:
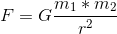
G es la constante gravitatoria. Si E2 se «asienta» sobre la Tierra, los centros de ambas masas están a 12742000 metros de distancia (dos veces el radio de la Tierra). Si rellenamos el resto de los números de la fórmula, obtenemos una fuerza de 1,4662378 * 10²⁵ Newton. Curiosamente, este número es unas cuantas veces MENOR de lo que habría sido si calculáramos (erróneamente) la fuerza como lo hacemos para los objetos «normales» que caen hacia la Tierra (multiplicando por 9,81). Aunque tengamos un cuerpo gravitatorio extra con su propia fuerza en el juego, la fuerza resultante es menor. ¿Cómo es posible? La respuesta es la distancia. Cuanto más se aleja uno de la Tierra, menor es la fuerza gravitatoria, y el centro de E2 está a 6371 kilómetros de la superficie de la Tierra.
Hay suficientes hormigas para llevar a cada humano.
De acuerdo, volvemos a nuestra pregunta original. Todavía necesitamos saber cuánta fuerza de elevación puede entregar una hormiga. Estoy encontrando cifras muy diferentes sobre cuánto puede levantar una hormiga, pero voy a usar el número de 50 veces su propio peso corporal. Combina esto con un peso de hormiga de, digamos, 2 miligramos. 50 veces su masa serían 100 miligramos, lo que da como resultado una fuerza de elevación de 0,000981 Newton. Necesitamos 1,4662378 * 10²⁵ Newton, así que necesitamos alrededor de 1,49 * 10²⁸ hormigas. Ahora bien, la cantidad total de hormigas en este planeta se ha estimado en 10¹⁶, así que no tenemos ni de lejos suficientes hormigas para levantar nuestro planeta. Curiosamente, teniendo en cuenta nuestro número, tenemos suficientes para llevar a todos los humanos. 10¹⁶ hormigas y 7,73 * 10⁹ humanos, tenemos más de un millón de hormigas por cada humano. Un millón de hormigas de 2 miligramos cada una tiene una masa total de 2 kg. Siendo capaces de cargar 50 veces su masa corporal, eso da como resultado 100 kilogramos. El humano medio es mucho más ligero que esto!