La fórmula de la velocidad media se utiliza para encontrar la tasa uniforme que implica que algo se desplace a un ritmo fijo y constante.
Por ejemplo, un coche viaja 3 horas. Recorre 30 millas en la primera hora, 45 millas en la segunda hora y 75 millas en la tercera hora.
Velocidad en la primera hora = 30 millas / hora
Velocidad en la segunda hora = 45 millas / hora
Velocidad en la tercera hora = 75 millas / hora
Tenemos tres velocidades diferentes en las tres horas de viaje.
Si queremos encontrar la velocidad media de todo el trayecto de tres horas, tenemos que encontrar el cociente entre la distancia total recorrida y el tiempo total empleado.
Es decir velocidad constante = (30 + 45 + 75) / 3
= 150 / 3
= 50 millas / hora
En base al ejemplo anterior, la fórmula para encontrar la velocidad media se da a continuación.
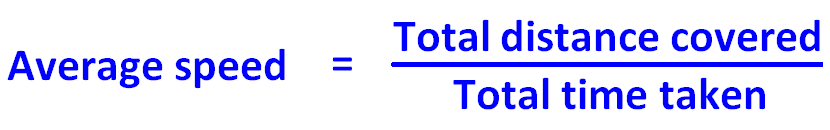
Si una persona viaja de A a B a cierta velocidad, digamos «x» millas por hora. Vuelve de B a A a una velocidad diferente, digamos «y» millas por hora. En ambos casos, cubre la misma distancia, pero a diferentes velocidades.
Entonces, la fórmula para hallar la velocidad media de todo el trayecto se da a continuación.
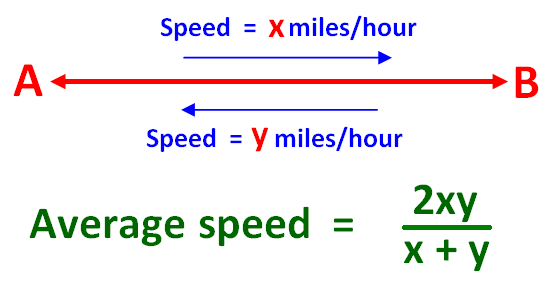
Fórmula de la velocidad media – Ejemplos
Ejemplo 1 :
David condujo durante 3 horas a una velocidad de 80 kilómetros por hora, durante 2 horas a 60 kilómetros por hora y durante 5 horas a una velocidad de 70 kilómetros por hora. Cuál fue su velocidad media durante todo el trayecto ?
Respuesta :
Paso 1 :
La fórmula de la velocidad media es
= Distancia total / Tiempo total empleado.
Y también, la fórmula para la distancia es
= Velocidad ⋅ Tiempo
Paso 2 :
La distancia recorrida en las primeras 3 horas es
= 50 ⋅ 3
= 150 millas
La distancia recorrida en las siguientes 2 horas es
= 60 ⋅ 2
= 120 millas
La distancia recorrida en las últimas 5 horas es
= 70 ⋅ 5
= 350 millas
Paso 3 :
Entonces, la distancia total es
= 150 + 120 + 350
= 620 millas
El tiempo total es
= 3 + 2 + 5
= 10 horas
Paso 4 :
Así, la velocidad media es
= 620 / 10
= 62
Así, la velocidad media de todo el trayecto es de 62 millas por hora.
Ejemplo 2 :
José viaja del lugar A al lugar B a una velocidad determinada. Cuando vuelve del lugar B al lugar A, su velocidad es de 60 millas por hora.Si la velocidad media de todo el viaje es de 72 millas por hora, halla su velocidad cuando viaja del lugar A al B.
Respuesta :
Paso 1 :
Sea «a» la velocidad del lugar A al B.
Velocidad del lugar B al A = 60 millas/hora
Paso 2 :
Aquí, en ambos sentidos, cubre la misma distancia.
Entonces, la fórmula para encontrar la velocidad media es
= 2xy / (x + y)
Paso 3 :
x —-> Velocidad del lugar A al B
x = a
y —-> Velocidad del lugar B al A
y = 60
Paso 4 :
Dado : La velocidad media es de 72 millas/hora.
(2 ⋅ a ⋅ 60) / (a + 60) = 72
120a = 72(a + 60)
120a = 72a + 4320
48a = 4320
a = 90
Entonces, la velocidad del lugar A al B es de 90 millas por hora.
Ejemplo 3 :
David viaja del lugar A al lugar B a una determinada velocidad. Cuando vuelve del lugar B al lugar A, aumenta su velocidad 2 veces. Si la velocidad constante para todo el viaje es de 80 millas por hora, encuentra su velocidad cuando viaja del lugar A al B.
Respuesta :
Paso 1 :
Sea «a» la velocidad del lugar A al B.
Entonces, la velocidad del lugar B al A = 2a
Paso 2 :
La distancia recorrida en ambos sentidos (A a B y B a A) es la misma.
Entonces, la fórmula para encontrar la velocidad media es
= 2xy / (x + y)
Paso 3 :
x —-> Velocidad del lugar A al B
x = a
y —-> Velocidad del lugar B al A
y = 2a
Paso 4 :
Dado : Velocidad media = 80 millas/hora
(2 ⋅ a ⋅ 2a) / (a + 2a) = 80
4a² / 3a = 80
4a / 3 = 80
a = 60
Entonces, la velocidad del lugar A al B es de 60 millas por hora.
Ejemplo 4 :
Una persona tarda 5 horas en viajar del lugar A al lugar B a razón de 40 millas por hora. Vuelve del lugar B al lugar A con un 25% más de velocidad. Halla la velocidad media de todo el trayecto.
Respuesta :
Paso 1 :
Velocidad ( de A a B) = 40 millas/hora
Velocidad ( de B a A) = 50 millas/hora (25% de aumento)
Paso 2 :
La distancia recorrida en ambos sentidos (de A a B y de B a A) es la misma.
Entonces, la fórmula para hallar la distancia media es
= 2xy / (x + y)
Paso 3 :
x —-> Velocidad del lugar A al B
x = 40
y —-> Velocidad del lugar B al A
y = 50
Paso 4 :
Velocidad media = (2 ⋅ 40 ⋅ 50) / (40 + 50)
Velocidad media = 44.44
Entonces, la velocidad media de todo el trayecto es de unos 44,44 kilómetros/hora.
Ejemplo 5 :
Velocidad ( de A a B ) = 20 millas/hora,
Velocidad (de B a C ) = 15 millas/hora,
Velocidad (C a D ) = 30 millas/hora
Si las distancias de A a B, B a C y C a D son iguales y se tarda 3 horas en viajar de A a B, halla la velocidad media de A a D.
Respuesta :
Paso 1 :
La fórmula para hallar la distancia es
= Tasa ⋅ Tiempo
La distancia de A a B es
= 20 ⋅ 3
= 60 millas
Dado : Las distancias de A a B, de B a C y de C a D son iguales.
La distancia total de A a D es
= 60 + 60 + 60
= 180 millas
Paso 2 :
La fórmula para hallar el tiempo es
= Distancia / Velocidad
Tiempo (A a B) = 60 / 20 = 3 horas
Tiempo (B a C) = 60 / 15 = 4 horas
Tiempo (C a D) = 60 / 30 = 2 horas
El tiempo total empleado desde A a D es
= 3 + 4 + 2
= 9 horas
Paso 3 :
La fórmula para hallar la velocidad media es
= Distancia total / Tiempo total tiempo
= 180 / 9
= 20
Entonces, la velocidad media de A a D es de 20 millas por hora.

Para obtener más problemas sobre la velocidad media,
Por favor, haz clic aquí
Aparte de las cosas dadas arriba, si necesitas cualquier otra cosa, por favor usa nuestra búsqueda personalizada de google aquí.
Si tienes algún comentario sobre nuestro contenido de matemáticas, por favor envíanos un correo :
Siempre apreciamos tus comentarios.
También puedes visitar las siguientes páginas web sobre diferentes cosas en matemáticas.
PROBLEMAS DE PALABRAS
Problemas de palabras de FCH y MCI
Problemas de palabras de ecuaciones simples
Problemas de palabras de ecuaciones lineales
Problemas de palabras de ecuaciones cuadráticas
Problemas de palabras sobre álgebra
Problemas de palabras sobre trenes
Problemas de palabras sobre área y perímetro
Problemas de palabras sobre variación directa y variación inversa
Problemas de palabras sobre precio unitario
Problemas de palabras sobre la tasa unitaria
Problemas de palabras sobre la comparación de tasas
Problemas de palabras sobre la conversión de unidades consuetudinarias
Problemas de palabras sobre la conversión de unidades métricas
Problemas de palabras sobre el simple interés
Problemas de palabras sobre interés compuesto
Problemas de palabras sobre tipos de ángulos
Problemas de palabras sobre ángulos complementarios y suplementarios
Problemas de palabras sobre hechos dobles
Problemas de palabras de trigonometría
Problemas de palabras de porcentajes
Problemas de palabras de pérdidas y ganancias
Problemas de palabras de marcas y tildes
Problemas de palabras de decimales
Problemas de palabras de fracciones.
Problemas de palabras sobre fracciones mixtas
Problemas de palabras de ecuaciones de un paso
Problemas de palabras de inecuaciones lineales
Problemas de palabras de relación y proporción
Problemas de palabras de tiempo y trabajo
Problemas de palabras sobre conjuntos y diagramas de Venn
Problemas de palabras sobre edades
Problemas de palabras sobre el teorema de Pitágoras
Problemas de palabras sobre el porcentaje de un número
Problemas de palabras sobre la velocidad constante
Problemas de palabras sobre la velocidad media
Problemas de palabras sobre la suma de los ángulos de un triángulo es de 180 grados
Otros temas
Accesos de pérdidas y ganancias
Accesos de porcentajes
Accesos de tablas de tiempos
Tiempo, velocidad y distancia
Accesos de razón y proporción
Dominio y rango de las funciones racionales
Dominio y rango de las funciones racionales con agujeros
Grafiar funciones racionales
Graficación de funciones racionales con huecos
Conversión de decimales repetidos en fracciones
Representación decimal de números racionales
Hallazgo de la raíz cuadrada mediante la división larga
L.C.M para resolver problemas de tiempo y trabajo
Traducción de los problemas de palabras en expresiones algebraicas
Recuperación cuando 2 potencia 256 se divide entre 17
Recuperación cuando 17 potencia 23 se dividido por 16
Suma de todos los números de tres cifras divisibles por 6
Suma de todos los números de tres cifras divisibles por 7
Suma de todos los números de tres cifras divisibles por 8
Suma de todos los números de tres cifras formados usando 1, 3, 4
Suma de los tres números de cuatro cifras formados con dígitos distintos de cero
Suma de los tres números de cuatro cifras formados con 0, 1, 2, 3
Suma de los tres números de cuatro cifras formados con 1, 2, 5, 6