Mostra avviso mobile Mostra tutte le note Nascondi tutte le note
Sezione 1-12 : Coordinate cilindriche
Come per lo spazio bidimensionale il sistema di coordinate standard \(\sinistra( {x,y,z} destra)\) è chiamato sistema di coordinate cartesiane. Nelle ultime due sezioni di questo capitolo vedremo alcuni sistemi di coordinate alternativi per lo spazio tridimensionale.
Iniziamo con il sistema di coordinate cilindriche. Questo è abbastanza semplice, in quanto non è altro che un’estensione delle coordinate polari in tre dimensioni. Non solo è un’estensione delle coordinate polari, ma lo estendiamo nella terza dimensione proprio come estendiamo le coordinate cartesiane nella terza dimensione. Tutto ciò che facciamo è aggiungere una \(z) come terza coordinata. Le coordinate \r\ e \theta\ sono le stesse delle coordinate polari.
Ecco uno schizzo di un punto in \({mathbb{R}^3}}.
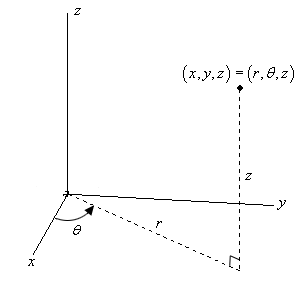
Le conversioni per \(x\) e \(y\) sono le stesse conversioni che abbiamo usato quando stavamo guardando le coordinate polari. Quindi, se abbiamo un punto in coordinate cilindriche, le coordinate cartesiane possono essere trovate usando le seguenti conversioni.
La terza equazione è solo un riconoscimento che la \(z)-coordinata di un punto in coordinate cartesiane e polari è la stessa.
Similmente, se abbiamo un punto in coordinate cartesiane, le coordinate cilindriche possono essere trovate utilizzando le seguenti conversioni.
Diamo una rapida occhiata ad alcune superfici in coordinate cilindriche.
- \(r = 5\)
- \({r^2} + {z^2} = 100\)
- \(z = r\)
Mostra tutte le soluzioni Nascondi tutte le soluzioni
In due dimensioni sappiamo che questo è un cerchio di raggio 5. Dato che ora siamo in tre dimensioni e non c’è \(z) nell’equazione, questo significa che può variare liberamente. Quindi, per ogni dato \(z) avremo un cerchio di raggio 5 centrato sull’asse \(z).
In altre parole, avremo un cilindro di raggio 5 centrato sull’asse \(z).
b \({r^2} + {z^2} = 100\) Mostra la soluzione
Questa equazione sarà facile da identificare una volta convertita in coordinate cartesiane.
\
Quindi, questa è una sfera centrata nell’origine con raggio 10.
c \(z = r\) Mostra Soluzione
Anche questa non sarà troppo male se riconvertiamo in cartesiane. Per ragioni che saranno evidenti alla fine, eleveremo prima al quadrato entrambi i lati, poi convertiremo.
\
Dalla sezione sulle superfici quadriche sappiamo che questa è l’equazione di un cono.