- Comportamento del campione medio (x-bar)
- La distribuzione del campione medio
Comportamento della media campionaria (x-bar)
Finora, abbiamo discusso il comportamento della statistica p-hat, la proporzione del campione, rispetto al parametro p, la proporzione della popolazione (quando la variabile di interesse è categorica).
Passiamo ora a esplorare il comportamento della statistica x-bar, la media del campione, rispetto al parametro μ (mu), la media della popolazione (quando la variabile di interesse è quantitativa).
Iniziamo con un esempio.
EXAMPLE 9: Comportamento delle medie del campione
Il peso alla nascita è registrato per tutti i bambini di una città. Il peso medio alla nascita è di 3.500 grammi, µ = mu = 3.500 g. Se raccogliamo molti campioni casuali di 9 bambini alla volta, come pensi che si comporteranno le medie del campione?
Ancora una volta, stiamo lavorando con una variabile casuale, poiché i campioni casuali avranno medie che variano in modo imprevedibile nel breve periodo, ma mostrano modelli nel lungo periodo.
In base alla nostra intuizione e a ciò che abbiamo imparato sul comportamento delle proporzioni del campione, potremmo aspettarci quanto segue sulla distribuzione delle medie del campione:
Centro: Alcune medie campionarie saranno sul lato basso – diciamo 3.000 grammi o giù di lì – mentre altre saranno sul lato alto – diciamo 4.000 grammi o giù di lì. Nel campionamento ripetuto, potremmo aspettarci che i campioni casuali facciano la media della popolazione sottostante di 3.500 g. In altre parole, la media delle medie dei campioni sarà µ (mu), proprio come la media delle proporzioni dei campioni era p.
Diffusione: Per i grandi campioni, potremmo aspettarci che le medie campionarie non si allontanino troppo dalla media della popolazione di 3.500. Le medie campionarie inferiori a 3.000 o superiori a 4.000 potrebbero essere sorprendenti. Per i campioni più piccoli, saremmo meno sorpresi da medie campionarie che variano abbastanza da 3.500. In altre parole, potremmo aspettarci una maggiore variabilità nelle medie campionarie per i campioni più piccoli. Quindi la dimensione del campione giocherà di nuovo un ruolo nella diffusione della distribuzione delle misure del campione, come abbiamo osservato per le proporzioni del campione.
Forma: Le medie campionarie più vicine a 3.500 saranno le più comuni, con medie campionarie lontane da 3.500 in entrambe le direzioni progressivamente meno probabili. In altre parole, la forma della distribuzione delle medie campionarie dovrebbe gonfiarsi al centro e assottigliarsi alle estremità con una forma in qualche modo normale. Questo, di nuovo, è quello che abbiamo visto quando abbiamo guardato le proporzioni del campione.
Commento:
- La distribuzione dei valori della media del campione (x-bar) in campioni ripetuti è chiamata distribuzione di campionamento di x-bar.
Guardiamo una simulazione:
I risultati che abbiamo trovato nelle nostre simulazioni non sono sorprendenti. La teoria avanzata della probabilità lo conferma affermando quanto segue:
La distribuzione di campionamento della media del campione
Se campioni casuali ripetuti di una data dimensione n sono presi da una popolazione di valori per una variabile quantitativa, dove la media della popolazione è μ (mu) e la deviazione standard della popolazione è σ (sigma) allora la media di tutte le medie del campione (x-bar) è la media della popolazione μ (mu).
Per quanto riguarda la diffusione di tutte le medie campionarie, la teoria detta il comportamento molto più precisamente che dire che c’è meno diffusione per campioni più grandi. Infatti, la deviazione standard di tutte le medie campionarie è direttamente correlata alla dimensione del campione, n, come indicato sotto.
![]()
Siccome la radice quadrata della dimensione del campione n appare nel denominatore, la deviazione standard diminuisce all’aumentare della dimensione del campione.
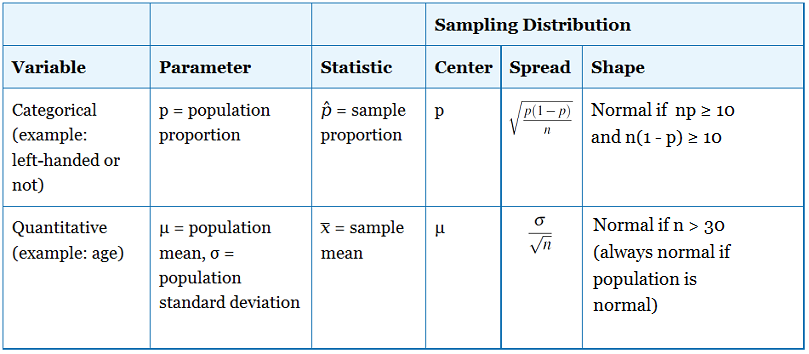
Confrontiamo e contrapponiamo ciò che ora sappiamo sulle distribuzioni di campionamento delle medie campionarie e delle proporzioni campionarie.

Ora studieremo la forma della distribuzione di campionamento delle medie campionarie. Quando stavamo discutendo la distribuzione di campionamento delle proporzioni del campione, abbiamo detto che questa distribuzione è approssimativamente normale se np ≥ 10 e n(1 – p) ≥ 10. In altre parole, avevamo una linea guida basata sulla dimensione del campione per determinare le condizioni in cui potevamo usare calcoli di probabilità normali per le proporzioni del campione.
Quando la distribuzione delle medie del campione sarà approssimativamente normale? Dipende dalla dimensione del campione?
Sembra ragionevole che una popolazione con una distribuzione normale avrà medie campionarie che sono distribuite normalmente anche per campioni molto piccoli. Lo abbiamo visto illustrato nella simulazione precedente con campioni di dimensione 10.
Cosa succede se la distribuzione della variabile nella popolazione è fortemente asimmetrica? Anche le medie dei campioni hanno una distribuzione asimmetrica? Se prendiamo campioni molto grandi, le medie campionarie diventeranno più distribuite normalmente?
Nella prossima simulazione, indagheremo queste domande.
Per riassumere, la distribuzione delle medie del campione sarà approssimativamente normale finché la dimensione del campione è abbastanza grande. Questa scoperta è probabilmente il singolo risultato più importante presentato nei corsi introduttivi di statistica. Viene enunciato formalmente come il Teorema del Limite Centrale.
Dipenderemo dal Teorema del Limite Centrale ancora e ancora per fare calcoli di probabilità normali quando usiamo le medie campionarie per trarre conclusioni sulla media di una popolazione. Ora sappiamo che possiamo farlo anche se la distribuzione della popolazione non è normale.
Quanto grande è la dimensione del campione di cui abbiamo bisogno per assumere che le medie del campione siano distribuite normalmente? Beh, dipende molto dalla distribuzione della popolazione, come abbiamo visto nella simulazione. La regola generale è che campioni di dimensioni pari o superiori a 30 avranno una distribuzione abbastanza normale, indipendentemente dalla forma della distribuzione della variabile nella popolazione.
Commento:
- Per le variabili categoriche, la nostra affermazione che le proporzioni campionarie sono approssimativamente normali per n abbastanza grandi è in realtà un caso speciale del Teorema del limite centrale. In questo caso, pensiamo ai dati come a 0 e 1 e la “media” di questi 0 e 1 è uguale alla proporzione che abbiamo discusso.
Prima di lavorare su alcuni esempi, confrontiamo e contrapponiamo ciò che ora sappiamo sulle distribuzioni di campionamento per medie e proporzioni campionarie.
ESEMPIO 10: Usare la distribuzione di campionamento di x-bar
La dimensione della famiglia negli Stati Uniti ha una media di 2,6 persone e una deviazione standard di 1,4 persone. Dovrebbe essere chiaro che questa distribuzione è inclinata a destra, poiché il valore più piccolo possibile è una famiglia di 1 persona, ma le famiglie più grandi possono essere davvero molto grandi.
(a) Qual è la probabilità che una famiglia scelta a caso abbia più di 3 persone?
Un’approssimazione normale non dovrebbe essere usata qui, perché la distribuzione delle dimensioni delle famiglie sarebbe notevolmente inclinata a destra. Non abbiamo abbastanza informazioni per risolvere questo problema.
(b) Qual è la probabilità che la dimensione media di un campione casuale di 10 famiglie sia superiore a 3?
Secondo gli standard di chiunque, 10 è una piccola dimensione del campione. Il Teorema del Limite Centrale non garantisce che la media di un campione proveniente da una popolazione asimmetrica sia approssimativamente normale, a meno che la dimensione del campione sia grande.
(c) Qual è la probabilità che la media di un campione casuale di 100 famiglie sia più di 3?
Ora possiamo invocare il Teorema del Limite Centrale: anche se la distribuzione della dimensione delle famiglie X è obliqua, la distribuzione della dimensione media delle famiglie del campione (x-bar) è approssimativamente normale per un campione di grandi dimensioni come 100. La sua media è uguale a quella della popolazione. La sua media è uguale alla media della popolazione, 2.6, e la sua deviazione standard è la deviazione standard della popolazione divisa per la radice quadrata della dimensione del campione:

Per trovare
![]()
standardizziamo 3 in uno z-score sottraendo la media e dividendo il risultato per la deviazione standard (della media del campione). Poi possiamo trovare la probabilità usando la calcolatrice o la tabella normale standard.

Le famiglie con più di 3 persone sono, ovviamente, abbastanza comuni, ma sarebbe estremamente insolito che la dimensione media di un campione di 100 famiglie sia più di 3.
Lo scopo della prossima attività è di fare pratica guidata nel trovare la distribuzione campionaria della media del campione (x-bar), e usarla per imparare la probabilità di ottenere certi valori di x-bar.
.