Come la viscosità influenza le pompe centrifughe
L’Hydraulic Institute ha pubblicato uno standard per tenere conto degli effetti della viscosità sulle prestazioni delle pompe centrifughe. Effects of Liquid Viscosity on Rotodynamic Centrifugal and Vertical Pump Performance-disponibile su www.estore.pumps.org-was rivisto nel 2010. Prima di questa pubblicazione, le correzioni di viscosità venivano fatte usando le tabelle di correzione della viscosità.
Il nuovo metodo è molto più facile da usare perché calcola automaticamente le correzioni di viscosità usando le formule fornite. La necessità di “occhio” dalle tabelle è stata rimossa, quindi il nuovo metodo è più accurato. La norma fornisce anche una bella descrizione di base del metodo, nonché i suoi limiti e i tipi di pompa e le caratteristiche di progettazione della pompa per cui la procedura è applicabile. Quanto segue è il risultato di una discussione tra diversi nostri lettori.
Che cosa sono i fluidi newtoniani?
Possiamo assumere che il petrolio greggio o i prodotti raffinati si comportino come fluidi newtoniani? Un’affermazione chiave è “La viscosità è una funzione solo delle condizioni del fluido, in particolare della sua temperatura”. L’acqua, il petrolio, la benzina, l’alcol e persino la glicerina sono esempi di fluidi newtoniani.
Esempi di fluidi non newtoniani sono i fanghi.Newtoniani sono gli slurry, sospensioni, gel e colloidi. Forse ci si potrebbe sentire a proprio agio con questa assunzione per il petrolio greggio e i prodotti raffinati. Ma il greggio pesante ad un certo punto (bassa temperatura) smette di comportarsi come un fluido newtoniano?
La maggior parte dei fluidi sono newtoniani con la definizione di base che la viscosità è costante con la velocità di taglio. Cos’è la velocità di taglio? È lo stress relativo imposto al fluido dal fluido in movimento. Consideriamo, per esempio, una girante chiusa di 10 pollici di diametro esterno (OD), con un gioco radiale di 0,010 pollici tra gli anelli di usura, che sono ad un diametro di 5 pollici. Se ruota a 3.600 rpm, allora la velocità periferica del metallo è di 78 piedi al secondo. Il fluido a contatto diretto con l’anello gira alla stessa velocità, secondo una condizione di non scorrimento. L’anello fermo è a 0,010 pollici di distanza dal movimento, quindi il gradiente di velocità è:
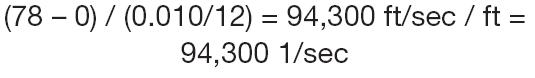
Questo è il tasso di taglio.
Per una girante aperta, la distanza è tra la paletta aperta della girante in rotazione e la parete del corpo. Ora la velocità periferica cambia lungo la posizione radiale della paletta (è a poco meno di 5 pollici rispetto al diametro esterno di, diciamo, 10 pollici). Un valore medio può essere stimato (il calcolo è simile a quello precedente), e la velocità di taglio sarà simile.
Sensibile al taglio, Non-Newtonian Fluids
I fluidi sensibili alI fluidi sensibili al taglio non amano questa azione di taglio. La colla, per esempio, diventa appiccicosa. La colla, tuttavia, non è pompata da pompe centrifughe ma più tipicamente da pompe ad ingranaggi. La velocità di taglio, tuttavia, funziona ancora anche lì: in uno spazio tra l’ingranaggio che gira e la parete, e tale spazio è anche tipicamente nell’intervallo di 0,005 pollici.
Tale velocità di taglio, tuttavia, di solito non è un problema, poiché la quantità di prodotto nello spazio è piccola e la “diluizione” complessiva da parte del fluido appiccicoso e danneggiato è trascurabile. In certi casi, però, è importante. Per esempio, se il fluido pompato da una pompa a ingranaggi è un’emulsione depositata su una pellicola fotografica, allora anche piccole imperfezioni possono causare macchie e difetti, e la pellicola finisce per essere difettosa. Il requisito della pompa è un pompaggio delicato con un basso livello di taglio. Le pompe a cavità progressiva funzionano meglio in questi casi.
In una pompa centrifuga con uno spazio tra la parete della girante e l’involucro di 0,5 pollici, la velocità di taglio è di 0,5 pollici.5 pollici, il tasso di taglio è:
![]()

Figura 1. Diversi tipi di fluidi
Newtoniano & Fluidi non newtoniani e viscosità
Con i fluidi newtoniani, la viscosità non dipende dalla velocità di taglio. Se l’olio pompato ha una viscosità di 300 cSt, per esempio, rimane tale a 3.600 rpm o a 1.800 rpm. La velocità di taglio cambia, ma la viscosità è ancora 300 cSt.
Tuttavia, per alcuni fluidi (non newtoniani), la viscosità cambia, sia verso l’alto che verso il basso, come mostrato nella Figura 1. Questi fluidi sono diluenti o tissotropici. Questo ha un effetto sulla potenza richiesta e può anche causare la degradazione del fluido, oltre ad avere un effetto (e di solito lo ha) sulla potenza. La potenza è forza per la velocità. La forza è lo stress per l’area. Lo stress è la viscosità per la velocità di taglio.
Per i fluidi dilatanti lo stress di taglio sale sempre, all’aumentare della viscosità e della velocità di taglio, ma per i fluidi tissotropici può andare in entrambi i modi. La velocità di taglio può non aumentare così velocemente come la diminuzione della viscosità, e il prodotto (stress) può aumentare, diminuire o rimanere circa lo stesso. Tutto dipende dal fluido pompato. Di solito, comunque, lo sforzo di taglio diminuisce. Ciò significa che anche la potenza della pompa diminuisce con la velocità di taglio. In altre parole, il fluido è inizialmente viscoso, ma una volta che inizia a muoversi, diventa meno viscoso, il che significa che è necessaria meno potenza per pomparlo.
Non considerare la potenza del driver (motore selezionato troppo piccolo) è comune. Viene dimensionato per la viscosità del fluido in movimento, ma poi un motore continua a scattare all’avvio perché è necessaria più potenza per far andare le cose. Il ketchup è un esempio, e questo è il motivo per cui si deve agitare la bottiglia come un pazzo al ristorante per farlo scorrere. Tuttavia, una volta che scorre, lo fa rapidamente.
Come sempre, un quiz di separazione. Perché è una regola “tipica” che le pompe centrifughe non funzionano bene al di sopra del numero magico di 500 centistokes di viscosità? Una risposta corretta vi darà un biglietto d’ingresso gratuito per la prossima sessione della Pump School: