Introduzione: PID Controller Design

In questo tutorial introdurremo una semplice, ma versatile, struttura di compensatore di feedback: il controllore Proporzionale-Integrale-Derivativo (PID). Il controllore PID è ampiamente utilizzato perché è molto comprensibile e perché è abbastanza efficace. Un’attrazione del controllore PID è che tutti gli ingegneri capiscono concettualmente la differenziazione e l’integrazione, quindi possono implementare il sistema di controllo anche senza una profonda comprensione della teoria del controllo. Inoltre, anche se il compensatore è semplice, è abbastanza sofisticato in quanto cattura la storia del sistema (attraverso l’integrazione) e anticipa il comportamento futuro del sistema (attraverso la differenziazione). Discuteremo l’effetto di ciascuno dei parametri PID sulla dinamica di un sistema ad anello chiuso e dimostreremo come usare un controllore PID per migliorare le prestazioni di un sistema.

I comandi MATLAB chiave usati in questo tutorial sono: tf , step , pid , feedback , pidtune

PID Overview

In questo tutorial, considereremo il seguente sistema a feedback unitario:

L’uscita di un controllore PID, che è uguale all’ingresso di controllo dell’impianto, è calcolato nel dominio del tempo dall’errore di retroazione come segue:

(1)$ u(t) = K_p e(t) + K_i \int e(t)dt + K_p \frac{de}{dt} $

Prima di tutto, diamo un’occhiata a come funziona il controllore PID in un sistema a circuito chiuso utilizzando lo schema mostrato sopra. La variabile ($e$) rappresenta l’errore di inseguimento, la differenza tra l’uscita desiderata ($r$) e quella effettiva ($y$). Questo segnale di errore ($e$) è alimentato al controllore PID, e il controllore calcola sia la derivata che l’integrale di questo segnale di errore rispetto al tempo. Il segnale di controllo ($u$) all’impianto è uguale al guadagno proporzionale ($K_p$) per la grandezza dell’errore più il guadagno integrale ($K_i$) per l’integrale dell’errore più il guadagno derivativo ($K_d$) per la derivata dell’errore.

Questo segnale di controllo ($u$) viene alimentato all’impianto e si ottiene la nuova uscita ($y$). La nuova uscita ($y$) viene quindi reimmessa e confrontata con il riferimento per trovare il nuovo segnale di errore ($e$). Il controllore prende questo nuovo segnale di errore e calcola un aggiornamento dell’ingresso di controllo. Questo processo continua mentre il controllore è in funzione.

La funzione di trasferimento di un controllore PID si trova prendendo la trasformata di Laplace dell’equazione (1).

(2)$ K_p + \frac {K_i} {s} + K_d s = \frac{K_d s^2 + K_p s + K_i} {s} $

dove $K_p$ = guadagno proporzionale, $K_i$ = guadagno integrale, e $K_d$ = guadagno derivativo.

Possiamo definire un controllore PID in MATLAB usando direttamente un modello di funzione di trasferimento, per esempio:

Kp = 1;Ki = 1;Kd = 1;s = tf('s');C = Kp + Ki/s + Kd*s
C = s^2 + s + 1 ----------- s Continuous-time transfer function.

In alternativa, possiamo usare l’oggetto pid di MATLAB per generare un controllore equivalente a tempo continuo come segue: 

C = pid(Kp,Ki,Kd)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 1, Ki = 1, Kd = 1 Continuous-time PID controller in parallel form.

Convertiamo l’oggetto pid in una funzione di trasferimento per verificare che dia lo stesso risultato di cui sopra:

tf(C)
ans = s^2 + s + 1 ----------- s Continuous-time transfer function.

Le caratteristiche dei termini P, I e D

Aumentare il guadagno proporzionale ($K_p$) ha l’effetto di aumentare proporzionalmente il segnale di controllo per lo stesso livello di errore. Il fatto che il controllore “spinga” di più per un dato livello di errore tende a far sì che il sistema ad anello chiuso reagisca più rapidamente, ma anche che vada più in eccesso. Un altro effetto dell’aumento di $K_p$ è che tende a ridurre, ma non ad eliminare, l’errore dello stato stazionario.

L’aggiunta di un termine derivativo al controllore ($K_d$) aggiunge la capacità del controllore di “anticipare” l’errore. Con un semplice controllo proporzionale, se $K_p$ è fisso, l’unico modo in cui il controllo aumenta è se l’errore aumenta. Con il controllo derivativo, il segnale di controllo può diventare grande se l’errore comincia a salire, anche quando la grandezza dell’errore è ancora relativamente piccola. Questa anticipazione tende ad aggiungere smorzamento al sistema, diminuendo così l’overshoot. L’aggiunta di un termine di derivazione, tuttavia, non ha alcun effetto sull’errore allo stato stazionario.

L’aggiunta di un termine integrale al controllore ($K_i$) tende a contribuire a ridurre l’errore allo stato stazionario. Se c’è un errore persistente e costante, l’integratore costruisce e costruisce, aumentando così il segnale di controllo e facendo scendere l’errore. Uno svantaggio del termine integrale, tuttavia, è che può rendere il sistema più lento (e oscillatorio) poiché quando il segnale di errore cambia di segno, l’integratore può impiegare un po’ di tempo per “srotolarsi”.

Gli effetti generali di ogni parametro del controllore ($K_p$$K_d$$K_i$) su un sistema ad anello chiuso sono riassunti nella tabella seguente. Notate che queste linee guida valgono in molti casi, ma non in tutti. Se volete veramente conoscere l’effetto del tuning dei singoli guadagni, dovrete fare più analisi, o dovrete eseguire dei test sul sistema reale.

CL RESPONSE
RISE TIME
OVERSHOOT
TEMPO DI IMPOSTAZIONE
S-S ERRORE
Kp
Riduzione
Aumento
Piccolo cambiamento
Riduzione
Ki
Riduci
Aumenta
Aumento
Riduzione
Kd
Piccolo cambiamento
Riduzione
Riduzione
Nessun cambiamento

Esempio di problema

Supponiamo di avere un semplice sistemasistema molla-ammortizzatore.

L’equazione di governo di questo sistema è

(3)$ m\ddot{x} + b\dot{x} + kx = F $

Prendendo la trasformata di Laplace dell’equazione di governo, otteniamo

(4)$ ms^{2}X(s) + bsX(s) + kX(s) = F(s) $

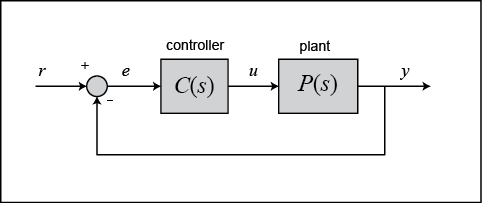
La funzione di trasferimento tra la forza di ingresso $F(s)$ e lo spostamento di uscita $X(s)$ diventa quindi

(5)$ \frac{X(s)}{F(s)} = \frac{1}{ms^2 + bs + k} $

Lascia

 m = 1 kg b = 10 N s/m k = 20 N/m F = 1 N

Sostituendo questi valori nella funzione di trasferimento di cui sopra

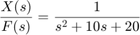
(6)$ \frac{X(s)}{F(s)} = \frac{1}{s^2 + 10s + 20} $

L’obiettivo di questo problema è mostrare come ciascuno dei termini, $K_p$$K_i$, e $K_d$, contribuisce ad ottenere gli obiettivi comuni di:

  • Tempo di salita veloce
  • Minimo overshoot
  • Errore zero allo stato stazionario

Risposta al passo ad anello aperto

Vediamo prima la risposta al passo ad anello aperto. Create un nuovo file m ed eseguite il seguente codice: 

s = tf('s');P = 1/(s^2 + 10*s + 20);step(P)

Il guadagno DC della funzione di trasferimento dell’impianto è 1/20, quindi 0,05 è il valore finale dell’uscita ad un ingresso a gradino unitario. Questo corrisponde a un errore di stato stazionario di 0,95, che è abbastanza grande. Inoltre, il tempo di salita è di circa un secondo, e il tempo di assestamento è di circa 1,5 secondi. Progettiamo un controllore che riduca il tempo di salita, riduca il tempo di assestamento, ed elimini l’errore di stato stazionario.

Controllo proporzionale

Dalla tabella mostrata sopra, vediamo che il controllore proporzionale ($K_p$) riduce il tempo di salita, aumenta l’overshoot, e riduce l’errore di stato costante.

La funzione di trasferimento ad anello chiuso del nostro sistema a retroazione unitaria con un controllore proporzionale è la seguente, dove $X(s)$ è la nostra uscita (uguale a $Y(s)$) e il nostro riferimento $R(s)$ è l’ingresso:

(7)$ T(s) = \frac{X(s)}{R(s)} = \frac{K_p}{s^2 + 10s + (20 + K_p)} $

Lasciate il guadagno proporzionale ($K_p$) uguale a 300 e cambiate il file m-come segue: 

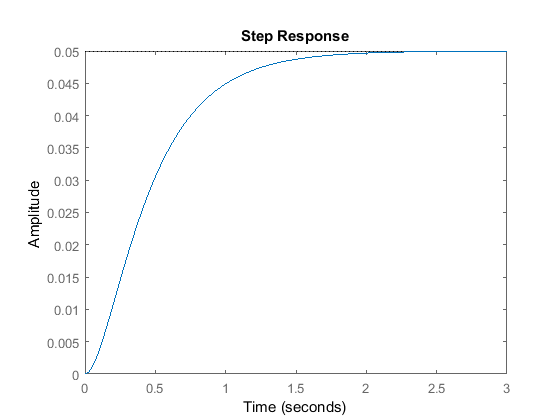
Kp = 300;C = pid(Kp)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp = 300 P-only controller.T = 300 ---------------- s^2 + 10 s + 320 Continuous-time transfer function.

Il grafico qui sopra mostra che il controllore proporzionale ha ridotto sia il tempo di salita che l’errore di stato stazionario, ha aumentato l’overshoot, e diminuito il tempo di assestamento di una piccola quantità.

Controllo proporzionale-derivativo

Ora diamo un’occhiata al controllo PD. Dalla tabella mostrata sopra, vediamo che l’aggiunta del controllo derivativo ($K_d$) tende a ridurre sia l’overshoot che il tempo di assestamento. La funzione di trasferimento ad anello chiuso del sistema dato con un controllore PD è:

(8)$ T(s) = \frac{X(s)}{R(s)} = \frac{K_d s + K_p}{s^2 + (10 + K_d) s + (20 + K_p)} $

Lasciate $K_p$ uguale a 300 come prima e lasciate $K_d$ uguale a 10. Inserite i seguenti comandi in un file m ed eseguitelo nella finestra di comando MATLAB. 

Kp = 300;Kd = 10;C = pid(Kp,0,Kd)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp + Kd * s with Kp = 300, Kd = 10 Continuous-time PD controller in parallel form.T = 10 s + 300 ---------------- s^2 + 20 s + 320 Continuous-time transfer function.

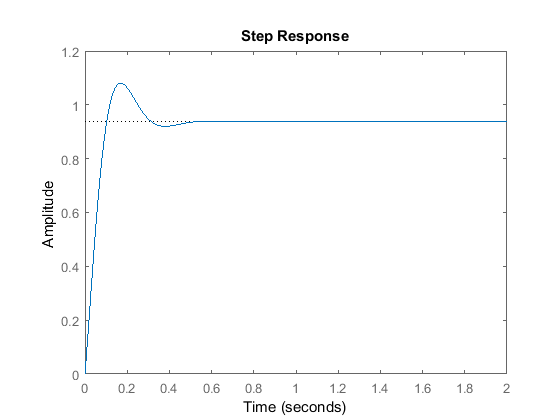
Questo grafico mostra che l’aggiunta del termine derivativo ha ridotto sia l’overshoot che il tempo di assestamento, e ha avuto un effetto trascurabile sul tempo di salita e sull’errore di stato stazionario.

Controllo proporzionale-integrale

Prima di procedere al controllo PID, esaminiamo il controllo PI. Dalla tabella, vediamo che l’aggiunta del controllo integrale ($K_i$) tende a diminuire il tempo di salita, aumenta sia l’overshoot che il tempo di assestamento, e riduce l’errore di stato stazionario. Per il sistema dato, la funzione di trasferimento ad anello chiuso con un controllore PI è:

(9)$ T(s) = \frac{X(s)}{R(s)} = \frac{K_p s + K_i}{s^3 + 10 s^2 + (20 + K_p )s + K_i} $

Riduciamo $K_p$ a 30, e lasciamo che $K_i$ sia uguale a 70. Create un nuovo file m e inserite i seguenti comandi. 

Kp = 30;Ki = 70;C = pid(Kp,Ki)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- s with Kp = 30, Ki = 70 Continuous-time PI controller in parallel form.T = 30 s + 70 ------------------------ s^3 + 10 s^2 + 50 s + 70 Continuous-time transfer function.

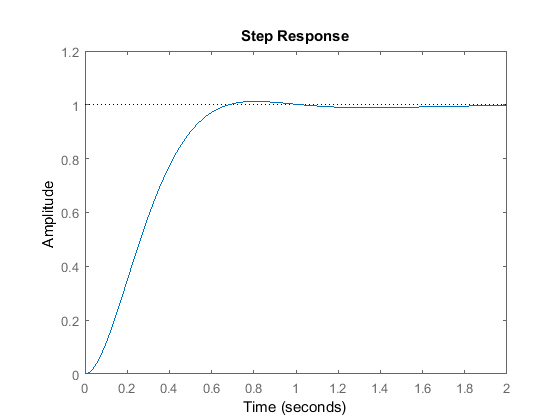
Eseguite questo file m nella finestra dei comandi MATLAB e dovreste generare il grafico di cui sopra. Abbiamo ridotto il guadagno proporzionale ($K_p$) perché il controller integrale riduce anche il tempo di salita e aumenta l’overshoot come fa il controller proporzionale (doppio effetto). La risposta di cui sopra mostra che il controllore integrale ha eliminato l’errore dello stato stazionario in questo caso.

Controllo proporzionale-integrale-derivativo

Esaminiamo ora il controllo PID. La funzione di trasferimento a circuito chiuso del sistema dato con un controllo PID è:

(10)$ T(s) = \frac{X(s)}{R(s)} = \frac{K_d s^2 + K_p s + K_i}{s^3 + (10 + K_d)s^2 + (20 + K_p)s + K_i } $

Dopo diverse iterazioni di tuning, i guadagni $K_p$$K_i$ = 300, e $K_d$ = 50 forniscono la risposta desiderata. Per confermare, inserite i seguenti comandi in un file m ed eseguitelo nella finestra di comando. Dovreste ottenere la seguente risposta di passo. 

Kp = 350;Ki = 300;Kd = 50;C = pid(Kp,Ki,Kd)T = feedback(C*P,1);t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 350, Ki = 300, Kd = 50 Continuous-time PID controller in parallel form.

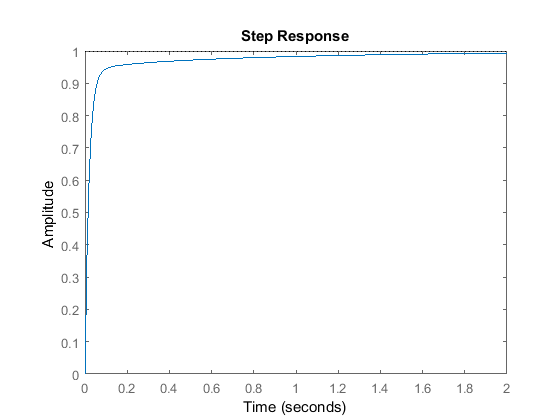
Ora abbiamo progettato un sistema ad anello chiuso senza overshoot, con un tempo di salita veloce e nessun errore allo stato stazionario.

Suggerimenti generali per la progettazione di un controllore PID

Quando si progetta un controllore PID per un dato sistema, seguire i passi indicati di seguito per ottenere la risposta desiderata.

  1. Ottenere una risposta ad anello aperto e determinare cosa deve essere migliorato
  2. Aggiungere un controllo proporzionale per migliorare il tempo di salita
  3. Aggiungere un controllo derivativo per ridurre l’overshoot
  4. Aggiungere un controllo integrale per ridurre l’errore di statostato stazionario
  5. Regolare ciascuno dei guadagni $K_p$$K_i$, e $K_d$ fino ad ottenere la risposta complessiva desiderata. Puoi sempre fare riferimento alla tabella mostrata in questa pagina “PID Tutorial” per scoprire quale controllore controlla quali caratteristiche.

Infine, tieni presente che non è necessario implementare tutti e tre i controllori (proporzionale, derivato e integrale) in un unico sistema, se non è necessario. Per esempio, se un controllore PI soddisfa i requisiti dati (come l’esempio precedente), allora non è necessario implementare un controllore derivativo sul sistema. Mantenete il controllore il più semplice possibile.

Un esempio di messa a punto di un controllore PI su un sistema fisico reale può essere trovato al seguente link. Questo esempio comincia anche a illustrare alcune sfide dell’implementazione del controllo, tra cui: saturazione del controllo, wind-up dell’integratore e amplificazione del rumore.

Tuning PID automatico

MATLAB fornisce strumenti per scegliere automaticamente i guadagni PID ottimali che rendono inutile il processo di prova ed errore descritto sopra. È possibile accedere all’algoritmo di tuning direttamente usando pidtune o attraverso una bella interfaccia grafica (GUI) usando pidTuner.

L’algoritmo di tuning automatico di MATLAB sceglie i guadagni PID per bilanciare le prestazioni (tempo di risposta, larghezza di banda) e la robustezza (margini di stabilità). Per default, l’algoritmo progetta per un margine di fase di 60 gradi.

Esploriamo questi strumenti automatici generando prima un controllore proporzionale per il sistema massa-molla-ammortizzatore inserendo il comando mostrato sotto. Nella sintassi mostrata, P è il modello di impianto generato in precedenza, e ‘p’ specifica che l’accordatore impiega un controllore proporzionale. 

 pidTuner(P,'p')

La finestra dell’interfaccia grafica di pidTuner, come quella mostrata sotto, dovrebbe apparire.

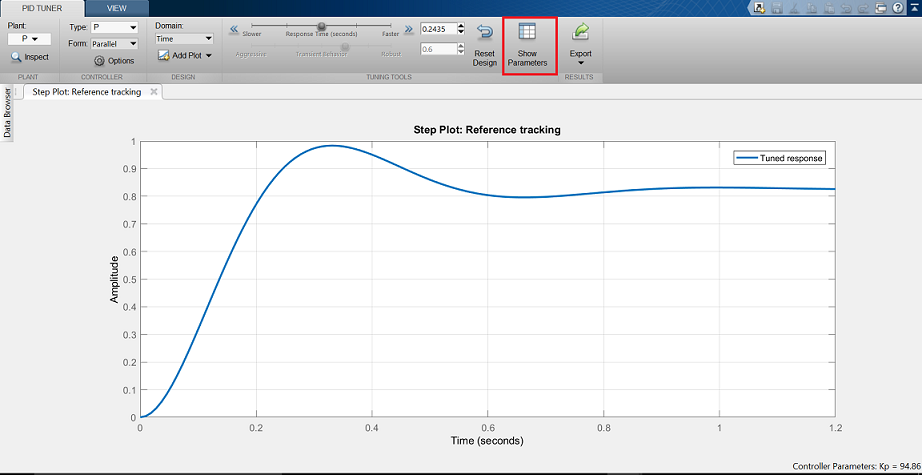
Nota che la risposta a passi mostrata è più lenta del controllore proporzionale che abbiamo progettato a mano. Ora clicchiamo sul pulsante Show Parameters in alto a destra. Come previsto, il guadagno proporzionale, $K_p$, è più piccolo di quello che abbiamo impiegato, $K_p$< 300.

Possiamo ora sintonizzare interattivamente i parametri del controller e vedere immediatamente la risposta risultante nella finestra dell’interfaccia grafica. Provate a trascinare il cursore del tempo di risposta a destra fino a 0,14 s, come mostrato nella figura sottostante. Questo fa sì che la risposta sia effettivamente più veloce, e possiamo vedere che $K_p$ è ora più vicino al valore scelto manualmente. Possiamo anche vedere altri parametri di performance e robustezza del sistema. Notate che prima che abbiamo regolato il cursore, il margine di fase di destinazione era di 60 gradi. Questo è il valore predefinito per il pidTuner e generalmente fornisce un buon equilibrio tra robustezza e prestazioni.

Ora proviamo a progettare un controller PID per il nostro sistema. Specificando il controllore precedentemente progettato o (baseline), C, come secondo parametro, pidTuner progetterà un altro controllore PID (invece di P o PI) e confronterà la risposta del sistema con il controllore automatico con quella della baseline. 

 pidTuner(P,C)

Vediamo nella finestra di output che il controllore automatico risponde più lentamente e mostra più overshoot rispetto alla linea di base. Ora scegliete l’opzione Domain: Frequency dalla barra degli strumenti, che rivela i parametri di regolazione del dominio della frequenza.

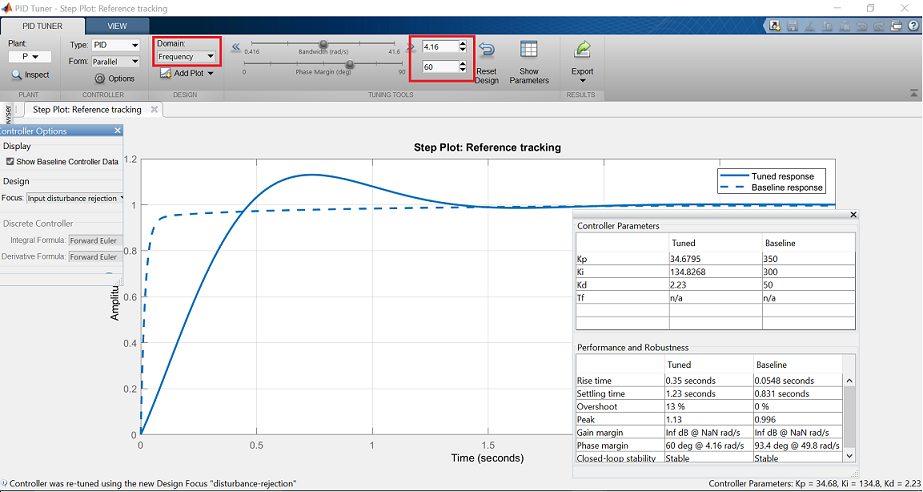
Ora digitate 32 rad/s per Bandwidth e 90 deg per Phase Margin, per generare un controllore con prestazioni simili alla linea di base. Tenete a mente che una maggiore larghezza di banda ad anello chiuso si traduce in un tempo di salita più veloce, e un margine di fase più grande riduce l’overshoot e migliora la stabilità del sistema.

Infine, notiamo che possiamo generare lo stesso controllore usando lo strumento a riga di comando pidtune invece della GUI pidTuner utilizzando la seguente sintassi. 

opts = pidtuneOptions('CrossoverFrequency',32,'PhaseMargin',90); = pidtune(P, 'pid', opts)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 320, Ki = 796, Kd = 32.2 Continuous-time PID controller in parallel form.info = struct with fields: Stable: 1 CrossoverFrequency: 32 PhaseMargin: 90

Pubblicato con MATLAB® 9.2

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *