I calcoli di PPT sono fatti nel calibro E, il che significa che il campo laser è preso come onde elettromagnetiche. Il tasso di ionizzazione può anche essere calcolato nel calibro A, che enfatizza la natura particellare della luce (assorbendo più fotoni durante la ionizzazione). Questo approccio è stato adottato dal modello Krainov basato sui lavori precedenti di Faisal e Reiss. Il tasso risultante è dato da
W K R A = ∑ n = N ∞ 2 π ω 2 p ( n – n o s c ) 2 ∫ d Ω | F T ( I K A R Ψ ( r ) | 2 J n 2 ( n f , n o s c 2 ) {displaystyle W_{KRA}=\sum _{n=N}^{\infty }2\pi \omega ^{2}p\sinistra(n-n_{\mathrm {osc} a destra)^{2}int \mathrm {d} \Omega \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità \falsità

dove:
- n i = E i / ω , {\displaystyle n_{i}=E_{i}/\omega ,}
- n o s c = U p / ω {displaystyle n_{mathrm {osc} = U_{p}/\omega }
con U p {displaystyle U_{p}}
essendo l’energia ponderomotrice,
- N = {\displaystyle N=}
è il numero minimo di fotoni necessari per ionizzare l’atomo,
- J n ( u , v ) {\displaystyle J_{n}(u,v)}
è la doppia funzione di Bessel,
- p = 2 ω ( n – n o s c – n i ) , {\displaystyle p={\sqrt {2\omega (n-n_{mathrm {osc} }-n_{i})},}
- n f = 2 n o s c / ω p cos ( θ ) {\displaystyle n_{f}=2{sqrt {n_{\mathrm {osc} / \omega }p\cos(\theta )}
l’angolo tra la quantità di moto dell’elettrone, p, e il campo elettrico del laser, F,
- FT è la trasformata tridimensionale di Fourier, e
- I K A R = ( 2 Z 2 n 2 F r ) n {displaystyle I_{KAR}=\left({\frac {2Z^{2}}{n^{2}}Fr}}\right)^{n}
incorpora la correzione Coulomb nel modello SFA.
Stabilizzazione atomica/intrappolamento della popolazioneModifica
Nel calcolare il tasso di MPI degli atomi si considerano solo le transizioni agli stati continui. Tale approssimazione è accettabile finché non c’è risonanza multifotonica tra lo stato fondamentale e alcuni stati eccitati. Tuttavia, nella situazione reale di interazione con i laser pulsati, durante l’evoluzione dell’intensità del laser, a causa del diverso spostamento di Stark degli stati terrestri ed eccitati c’è la possibilità che qualche stato eccitato vada in risonanza multifotonica con lo stato terrestre. Nell’immagine dell’atomo vestito, lo stato fondamentale vestito da m {displaystyle m}

fotoni e lo stato risonante subiscono un incrocio evitato all’intensità di risonanza I r {displaystyle I_{r}}

. La distanza minima, V m {displaystyle V_{m}

, all’attraversamento evitato è proporzionale alla frequenza di Rabi generalizzata, Γ ( t ) = Γ m I ( t ) m / 2 {\displaystyle \Gamma (t)=\Gamma _{m}I(t)^{m/2}}

accoppiando i due stati. Secondo Story et al. la probabilità di rimanere nello stato di terra, P g {displaystyle P_{g}}

, è data da P g = exp ( – 2 π W m 2 d W / d t ) {displaystyle P_{g}=exp \left(-{frac {2\pi W_{m}^{2}}{\mathrm {d} W/\mathrm {d} t}}} a destra)}

dove W {displaystyle W}

è la differenza di energia dipendente dal tempo tra i due stati vestiti. Nell’interazione con un impulso breve, se la risonanza dinamica è raggiunta nella parte ascendente o discendente dell’impulso, la popolazione rimane praticamente nello stato fondamentale e l’effetto delle risonanze multifotone può essere trascurato. Tuttavia, se gli stati vanno in risonanza al picco dell’impulso, dove d W / d t = 0 {displaystyle \mathrm {d} W / d t=0} t=0}

, allora lo stato eccitato è popolato. Dopo essere stato popolato, poiché il potenziale di ionizzazione dello stato eccitato è piccolo, ci si aspetta che l’elettrone venga ionizzato istantaneamente.
Nel 1992, de Boer e Muller hanno dimostrato che gli atomi di Xe sottoposti a brevi impulsi laser potevano sopravvivere negli stati altamente eccitati 4f, 5f e 6f . Si credeva che questi stati fossero stati eccitati dallo spostamento dinamico di Stark dei livelli in risonanza multifotonica con il campo durante la parte ascendente dell’impulso laser. La successiva evoluzione dell’impulso laser non ha ionizzato completamente questi stati lasciando alcuni atomi altamente eccitati. Ci riferiremo a questo fenomeno come “population trapping”.

Citiamo il calcolo teorico che la ionizzazione incompleta avviene ogni volta che c’è un’eccitazione risonante parallela in un livello comune con perdita di ionizzazione. Consideriamo uno stato come il 6f di Xe che consiste di 7 livelli quasi-degnerati nell’intervallo della larghezza di banda del laser. Questi livelli insieme al continuo costituiscono un sistema lambda. Il meccanismo dell’intrappolamento di tipo lambda è presentato schematicamente in figura. Nella parte ascendente dell’impulso (a) lo stato eccitato (con due livelli degenerati 1 e 2) non sono in risonanza multifotonica con lo stato fondamentale. L’elettrone viene ionizzato attraverso l’accoppiamento multifotonico con il continuo. All’aumentare dell’intensità dell’impulso, lo stato eccitato e il continuo sono spostati in energia a causa dello spostamento di Stark. Al picco dell’impulso (b) gli stati eccitati vanno in risonanza multifotonica con lo stato fondamentale. Quando l’intensità comincia a diminuire (c), i due stati sono accoppiati attraverso il continuo e la popolazione è intrappolata in una sovrapposizione coerente dei due stati. Sotto l’azione successiva dello stesso impulso, a causa dell’interferenza nelle ampiezze di transizione del sistema lambda, il campo non può ionizzare completamente la popolazione e una frazione della popolazione sarà intrappolata in una sovrapposizione coerente dei livelli quasi degenerati. Secondo questa spiegazione, gli stati con un momento angolare più alto – con più sottolivelli – avrebbero una maggiore probabilità di intrappolare la popolazione. In generale la forza dell’intrappolamento sarà determinata dalla forza dell’accoppiamento a due fotoni tra i livelli quasi degenerati attraverso il continuum. Nel 1996, usando il laser molto stabile e minimizzando gli effetti di mascheramento dell’espansione della regione focale con l’aumentare dell’intensità, Talebpour et al. hanno osservato strutture sulle curve degli ioni singolarmente carichi di Xe, Kr e Ar. Queste strutture sono state attribuite all’intrappolamento degli elettroni nel forte campo laser. Una dimostrazione più inequivocabile dell’intrappolamento della popolazione è stata riportata da T. Morishita e C. D. Lin.
Ionizzazione multipla non sequenzialeModifica
Il fenomeno della ionizzazione non sequenziale (NSI) di atomi esposti a intensi campi laser è stato oggetto di molti studi teorici e sperimentali dal 1983. Il lavoro pionieristico è iniziato con l’osservazione di una struttura a “ginocchio” sulla curva del segnale dello ione Xe2+ rispetto all’intensità da parte di L’Huillier et al. Dal punto di vista sperimentale, la doppia ionizzazione NS si riferisce a processi che in qualche modo aumentano il tasso di produzione di ioni con carica doppia di un fattore enorme a intensità inferiori all’intensità di saturazione dello ione con carica singola. Molti, d’altra parte, preferiscono definire la NS come un processo attraverso il quale due elettroni sono ionizzati quasi simultaneamente. Questa definizione implica che oltre al canale sequenziale A + L – > A + + L – > A + + {\displaystyle A+L->A^{+}+L->A^{++}

c’è un altro canale A + L – > A + + {\displaystyle A+L->A^{++}

che è il principale contributo alla produzione di ioni doppiamente carichi a basse intensità. La prima osservazione di un NSI triplo nell’argon che interagisce con un laser da 1 µm fu riportata da Augst et al. Più tardi, studiando sistematicamente l’NSI di tutti gli atomi di gas rari, fu osservato il quadruplo NSI di Xe. La conclusione più importante di questo studio fu l’osservazione della seguente relazione tra il tasso di NSI a qualsiasi stato di carica e il tasso di ionizzazione tunnel (previsto dalla formula ADK) agli stati di carica precedenti; W N S ( A n + ) = ∑ i = 1 n – 1 α n ( λ ) W A D K ( A i + ) {\displaystyle W_{NS}(A^{n+})=\sum _{i=1}^{n-1}{alpha _{n}\left(\lambda \right)W_{ADK}\left(A^{i+}\right)}

dove W A D K ( A i + ) {\displaystyle W_{ADK} a sinistra(A^{i+} a destra)}

è il tasso di tunneling quasi-statico verso lo stato di carica i’th e α n ( λ ) {displaystyle \alpha _{n}(\lambda )}

sono delle costanti che dipendono dalla lunghezza d’onda del laser (ma non dalla durata dell’impulso).
Sono stati proposti due modelli per spiegare la ionizzazione non sequenziale: il modello shake-off e il modello di ridispersione degli elettroni. Il modello shake-off (SO), proposto per la prima volta da Fittinghoff et al., è adottato dal campo della ionizzazione degli atomi da raggi X e proiettili di elettroni dove il processo SO è uno dei principali meccanismi responsabili della ionizzazione multipla degli atomi. Il modello SO descrive il processo NS come un meccanismo in cui un elettrone viene ionizzato dal campo laser e la partenza di questo elettrone è così rapida che gli elettroni rimanenti non hanno abbastanza tempo per adattarsi ai nuovi stati energetici. Pertanto, c’è una certa probabilità che, dopo la ionizzazione del primo elettrone, un secondo elettrone venga eccitato a stati con energia più alta (shake-up) o addirittura ionizzato (shake-off). Dobbiamo menzionare che, fino ad ora, non c’è stato nessun calcolo quantitativo basato sul modello SO, e il modello è ancora qualitativo.
Il modello di rescattering degli elettroni è stato sviluppato indipendentemente da Kuchiev, Schafer et al, Corkum, Becker e Faisal e Faisal e Becker. Le caratteristiche principali del modello possono essere comprese facilmente dalla versione di Corkum. Il modello di Corkum descrive la ionizzazione NS come un processo per cui un elettrone viene ionizzato in tunnel. L’elettrone poi interagisce con il campo laser dove viene accelerato lontano dal nucleo nucleare. Se l’elettrone è stato ionizzato in una fase appropriata del campo, passerà vicino alla posizione dello ione rimanente mezzo ciclo dopo, dove può liberare un ulteriore elettrone per impatto elettronico. Solo la metà delle volte l’elettrone viene rilasciato con la fase appropriata e l’altra metà non torna mai al nucleo nucleare. L’energia cinetica massima che l’elettrone di ritorno può avere è 3,17 volte il potenziale ponderomotore ( U p {\displaystyle U_{p}}

) del laser. Il modello di Corkum pone un limite di cut-off sull’intensità minima ( U p {displaystyle U_{p}}

è proporzionale all’intensità) in cui può avvenire la ionizzazione dovuta al re-scattering.
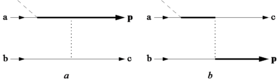
Il modello di ri-scattering nella versione di Kuchiev (modello di Kuchiev) è quantomeccanico. L’idea di base del modello è illustrata dai diagrammi di Feynman nella figura a. Prima entrambi gli elettroni sono nello stato fondamentale di un atomo. Le linee marcate a e b descrivono gli stati atomici corrispondenti. Poi l’elettrone a viene ionizzato. L’inizio del processo di ionizzazione è mostrato dall’intersezione con una linea tratteggiata inclinata, dove avviene il MPI. La propagazione dell’elettrone ionizzato nel campo laser, durante la quale assorbe altri fotoni (ATI), è mostrata dalla linea spessa piena. La collisione di questo elettrone con lo ione atomico padre è mostrata da una linea verticale tratteggiata che rappresenta l’interazione Coulomb tra gli elettroni. Lo stato segnato con c descrive l’eccitazione dello ione in uno stato discreto o continuo. La figura b descrive il processo di scambio. Il modello di Kuchiev, contrariamente al modello di Corkum, non prevede alcuna soglia di intensità per il verificarsi della ionizzazione NS.
Kuciev non ha incluso gli effetti Coulomb sulla dinamica dell’elettrone ionizzato. Questo ha portato alla sottostima del tasso di doppia ionizzazione di un fattore enorme. Ovviamente, nell’approccio di Becker e Faisal (che è equivalente al modello di Kuchiev nello spirito), questo inconveniente non esiste. Infatti, il loro modello è più esatto e non soffre del gran numero di approssimazioni fatte da Kuchiev. I loro risultati di calcolo si adattano perfettamente ai risultati sperimentali di Walker et al. Becker e Faisal sono stati in grado di adattare i risultati sperimentali sugli NSI multipli di atomi di gas rari utilizzando il loro modello. Di conseguenza, la ricaduta degli elettroni può essere presa come il meccanismo principale per il verificarsi del processo NSI.
Ionizzazione multifotonica degli elettroni di valenza interna e frammentazione delle molecole poliatomicheModifica
La ionizzazione degli elettroni di valenza interna è responsabile della frammentazione delle molecole poliatomiche in forti campi laser. Secondo un modello qualitativo la dissociazione delle molecole avviene attraverso un meccanismo a tre fasi:
- MPI di elettroni dagli orbitali interni della molecola che si traduce in uno ione molecolare in livelli ro-vibrazionali di uno stato elettronico eccitato;
- Rapida transizione senza radiazioni ai livelli ro-vibrazionali alti di uno stato elettronico inferiore; e
- Successiva dissociazione dello ione in diversi frammenti attraverso vari canali di frammentazione.







