Come gestire gli eventi dipendenti
La vita è piena di eventi casuali! Hai bisogno di “sentirli” per essere una persona intelligente e di successo.
Eventi indipendenti
Gli eventi possono essere “indipendenti”, cioè ogni evento non è influenzato da nessun altro evento.

Esempio: Lancio di una moneta.
Ogni lancio di una moneta è una cosa perfettamente isolata.
Quello che ha fatto in passato non influenzerà il lancio attuale.
La probabilità è semplicemente 1 su 2, o 50%, proprio come ogni lancio della moneta.
Quindi ogni lancio è un evento indipendente.
Eventi dipendenti
Ma gli eventi possono anche essere “dipendenti” … il che significa che possono essere influenzati da eventi precedenti …

Esempio: Biglie in un sacchetto
2 biglie blu e 3 rosse sono in un sacchetto.
Quali sono le probabilità di ottenere una biglia blu?
La probabilità è 2 su 5
Ma dopo averne tolta una le probabilità cambiano!
Quindi la prossima volta:
se abbiamo avuto una biglia rossa prima, allora la probabilità di una biglia blu dopo è 2 su 4
se abbiamo avuto una biglia blu prima, allora la probabilità di una biglia blu dopo è 1 su 4
Questo perché stiamo rimuovendo biglie dal sacchetto.
Quindi l’evento successivo dipende da ciò che è successo nell’evento precedente, ed è chiamato dipendente.
Sostituzione
Nota: se sostituiamo le biglie nel sacchetto ogni volta, allora le probabilità non cambiano e gli eventi sono indipendenti:
- Con la sostituzione: gli eventi sono indipendenti (le probabilità non cambiano)
- Senza sostituzione: gli eventi sono dipendenti (le probabilità cambiano)
Gli eventi dipendenti sono quelli che guardiamo qui.
Diagramma ad albero
Un diagramma ad albero: è un modo meraviglioso per immaginare cosa sta succedendo, quindi costruiamone uno per il nostro esempio delle biglie.
C’è una probabilità di 2/5 di estrarre una biglia blu, e una probabilità di 3/5 per la rossa:
Possiamo fare un passo avanti e vedere cosa succede quando prendiamo una seconda biglia:
Se una biglia blu è stata selezionata per prima c’è ora 1/4 di possibilità di ottenere una biglia blu e 3/4 di ottenere una biglia rossa.
Se una biglia rossa è stata selezionata per prima, ora c’è una probabilità di 2/4 di ottenere una biglia blu e una probabilità di 2/4 di ottenere una biglia rossa.
Ora possiamo rispondere a domande come “Quali sono le probabilità di estrarre 2 biglie blu?”
Risposta: è una probabilità di 2/5 seguita da una probabilità di 1/4:
Hai visto come abbiamo moltiplicato le probabilità? E abbiamo ottenuto 1/10 come risultato.
La probabilità di estrarre 2 biglie blu è 1/10
Notazione
Adoriamo la notazione in matematica! Significa che possiamo usare la potenza dell’algebra per giocare con le idee. Quindi ecco la notazione per la probabilità:
P(A) significa “Probabilità dell’evento A”
Nel nostro esempio delle biglie l’evento A è “ottenere un marmo blu per primo” con una probabilità di 2/5:
P(A) = 2/5
E l’evento B è “ottenere un marmo blu per secondo” … ma per questo abbiamo 2 scelte:
- Se abbiamo ottenuto un Blue Marble prima la probabilità è ora 1/4
- Se abbiamo ottenuto un Red Marble prima la probabilità è ora 2/4
Così dobbiamo dire quale vogliamo, e usare il simbolo “|” per significare “dato”:
P(B|A) significa “Evento B dato Evento A”
In altre parole, l’evento A è già accaduto, ora qual è la probabilità dell’evento B?
P(B|A) si chiama anche “Probabilità condizionata” di B dato A.
E nel nostro caso:
P(B|A) = 1/4
Quindi la probabilità di ottenere 2 biglie blu è:
E lo scriviamo come
“La probabilità dell’evento A e dell’evento B è uguale
alla probabilità dell’evento A per la probabilità dell’evento B dato l’evento A”
Facciamo il prossimo esempio usando solo la notazione:
Esempio: Pescare 2 Re da un mazzo
L’evento A è pescare un Re per primo, e l’evento B è pescare un Re per secondo.
Per la prima carta la probabilità di pescare un Re è 4 su 52 (ci sono 4 Re in un mazzo di 52 carte):
P(A) = 4/52
Ma dopo aver rimosso un Re dal mazzo la probabilità che la seconda carta pescata sia un Re è minore (solo 3 delle 51 carte rimaste sono Re):
P(B|A) = 3/51
E quindi:
P(A e B) = P(A) x P(B|A) = (4/52)x (3/51) = 12/2652 = 1/221
Quindi la probabilità di ottenere 2 Re è 1 su 221, o circa 0.5%
Trovare i dati nascosti
Utilizzando l’algebra possiamo anche “cambiare il soggetto” della formula, come questo:
| Inizia con: | P(A e B) = P(A) x P(B|A) | |
| Scambiate i lati: | P(A) x P(B|A) = P(A e B) | |
| Dividete per P(A): | P(B|A) = P(A e B) / P(A) |
E abbiamo un’altra formula utile:
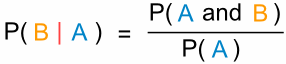
“La probabilità dell’evento B dato l’evento A è uguale
alla probabilità dell’evento A e dell’evento B diviso la probabilità dell’evento A
Esempio: Gelato
Al 70% dei tuoi amici piace il cioccolato, e al 35% piace il cioccolato E piace la fragola.
Quale percentuale di quelli a cui piace il cioccolato piace anche la fragola?
P(fragola|cioccolato) = P(cioccolato e fragola) / P(cioccolato)
50% dei tuoi amici a cui piace il cioccolato piace anche la fragola

Grande esempio: Partita di calcio
Sei fuori a calcio, e vuoi essere il portiere, ma questo dipende da chi è l’allenatore oggi:
- con l’allenatore Sam la probabilità di essere portiere è 0,5
- con l’allenatore Alex la probabilità di essere portiere è 0.3
Sam è allenatore più spesso … circa 6 su 10 partite (una probabilità di 0,6).
Quindi, qual è la probabilità che tu sia un portiere oggi?
Costruiamo un diagramma ad albero. Prima mostriamo i due possibili allenatori: Sam o Alex:
La probabilità di ottenere Sam è 0,6, quindi la probabilità di Alex deve essere 0,4 (insieme la probabilità è 1)
Ora, se si ottiene Sam, c’è 0,5 probabilità di essere portiere (e 0.5 di non essere portiere):
Se si ottiene Alex, c’è 0,3 probabilità di essere portiere (e 0.7 no):
Il diagramma ad albero è completo, ora calcoliamo le probabilità complessive. Ricordate che:
P(A e B) = P(A) x P(B|A)
Ecco come fare per il ramo “Sam, Sì”:
(Quando prendiamo lo 0.6 possibilità che Sam sia allenatore moltiplicato per lo 0,5 che Sam ti lasci fare il portiere, ci ritroviamo con una probabilità di 0,3.)
Ma non abbiamo ancora finito! Non abbiamo incluso Alex come Allenatore:
Uno 0,4 di probabilità di Alex come Allenatore, seguito da uno 0,3 dà 0,12
E i due rami “Sì” dell’albero insieme fanno:
0,3 + 0,12 = 0.42 probabilità di essere un Portiere oggi
(Questo è un 42% di probabilità)
Controlla
Un ultimo passo: completa i calcoli e assicurati che sommino a 1:
0.3 + 0.3 + 0.12 + 0.28 = 1
Sì, si sommano a 1, quindi sembra giusto.
Amici e numeri casuali
Ecco un altro esempio abbastanza diverso di probabilità condizionata.
4 amici (Alex, Blake, Chris e Dusty) scelgono ciascuno un numero casuale tra 1 e 5. Qual è la probabilità che uno di loro abbia scelto lo stesso numero?
Aggiungiamo i nostri amici uno alla volta…
Primo, qual è la probabilità che Alex e Blake abbiano lo stesso numero?
Blake confronta il suo numero con quello di Alex. C’è una possibilità su 5 di corrispondenza.
Come diagramma ad albero:
Nota: “Sì” e “No” insieme fanno 1
(1/5 + 4/5 = 5/5 = 1)
Ora, includiamo Chris …
Ma ora ci sono due casi da considerare:
- Se Alex e Blake corrispondono, allora Chris ha un solo numero da confrontare.
- Ma se Alex e Blake non corrispondono, Chris ha due numeri da confrontare.
E otteniamo questo:
Per la linea superiore (Alex e Blake hanno avuto una corrispondenza) abbiamo già una corrispondenza (una probabilità di 1/5).
Ma per “Alex e Blake non sono stati abbinati” c’è ora una probabilità di 2/5 che Chris sia abbinato (perché Chris può abbinare il suo numero sia con Alex che con Blake).
E possiamo calcolare la probabilità combinata moltiplicando le probabilità che ci sono volute per arrivare lì:
Seguendo il percorso “No, Sì” … c’è una probabilità di 4/5 di No, seguita da una probabilità di 2/5 di Sì:
Seguendo il percorso “No, No” … c’è un 4/5 di probabilità di No, seguito da un 3/5 di probabilità di No:
Si noti anche che quando sommiamo tutte le probabilità otteniamo ancora 1 (un buon controllo che non abbiamo fatto un errore):
(5/25) + (8/25) + (12/25) = 25/25 = 1
Ora cosa succede quando includiamo Dusty?
È la stessa idea, solo più di questa:
OK, sono tutti e 4 gli amici, e le possibilità di “Sì” insieme fanno 101/125:
Risposta: 101/125
Ma qui c’è qualcosa di interessante … se seguiamo il percorso “No” possiamo saltare tutti gli altri calcoli e semplificarci la vita:
Le probabilità di non corrispondenza sono:
(4/5) × (3/5) × (2/5) = 24/125
Quindi le probabilità di corrispondenza sono:
1 – (24/125) = 101/125
(E non abbiamo davvero bisogno di un diagramma ad albero per questo!)
















