Che cos’è la probabilità congiunta?
La probabilità congiunta è un tipo di misura trovata calcolando la probabilità che due eventi accadano insieme. In altre parole, è la probabilità che l’evento X accada contemporaneamente all’evento Y, come un’intersezione di due eventi.
Probabilità congiunta per eventi dipendenti
Per misurare la probabilità congiunta, entrambi gli eventi devono accadere nello stesso momento e devono essere indipendenti l’uno dall’altro. Ciò significa che la probabilità congiunta per eventi dipendenti non può essere determinata.
Si dice che si vuole determinare se pioverà nello stesso momento in cui ci sono le nuvole in cielo. Questi due eventi sono dipendenti l’uno dall’altro perché quando piove, molto probabilmente ci sarà la presenza di nuvole. Pertanto, questi eventi sono dipendenti l’uno dall’altro.
Invece della probabilità congiunta, la probabilità condizionata dovrebbe essere usata per gli eventi dipendenti.
Probabilità congiunta per eventi indipendenti
Come detto, per determinare la probabilità congiunta, entrambi gli eventi devono essere indipendenti l’uno dall’altro. Per esempio, la probabilità di ottenere “croce” o “testa” nel lancio di una moneta sono eventi indipendenti. In altre parole, la probabilità di ottenere una coda al primo lancio non avrà un impatto sulla probabilità di ottenere una testa quando si lancia la moneta una seconda volta.
Come calcolare la probabilità congiunta
Quando si impara a calcolare la probabilità congiunta, è fondamentale capire che la formula richiede che i due eventi siano indipendenti tra loro. Ciò significa che il risultato di un evento non può influenzare l’impatto del risultato dell’altro evento. Prima di calcolare la probabilità congiunta, chiedetevi se il risultato di un evento influenzerà il risultato dell’altro.
Siccome la probabilità congiunta può essere descritta come “l’intersezione di due eventi”, la formula includerà i due – e come possono intersecarsi.
Nella formula qui sotto, vedrete il simbolo “∩” usato per rappresentare un’intersezione. Per gli studenti più visivi, usare un diagramma di Venn è il modo migliore per illustrare come due eventi possono intersecarsi insieme.
Formula della probabilità congiunta
La formula della probabilità congiunta è la seguente:
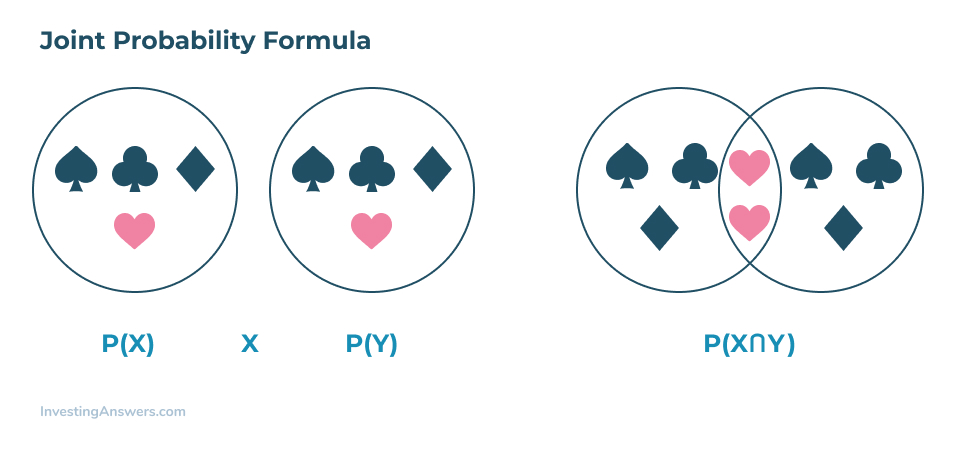
In questa formula, X e Y rappresentano entrambi due diversi eventi che si intersecano, e P è uguale alla probabilità di unione di entrambi X e Y.
Altri modi per esprimere la formula della probabilità congiunta includono anche P( X e Y) e P(XY).
Esempio di probabilità congiunta #1
Diciamo che si voglia calcolare la probabilità congiunta per un lancio di moneta dove si può ottenere una coda (evento X) seguita da una testa (evento Y).
In questo caso, la probabilità dell’evento X è del 50% (o 0,5) e la probabilità dell’evento Y è anche del 50%. Ora possiamo inserire i numeri nella formula:
P(0.5 x 0.5) = 0.25 o 25%
Questo significa che la probabilità congiunta di ottenere una coda e poi una testa nel lancio della moneta è del 25%.
Esempio di probabilità congiunta #2
Stai lanciando un dado e vuoi capire la probabilità congiunta di far uscire il numero sei due volte di seguito. La probabilità di seguire un sei la prima volta è 1/6, poiché ci sono solo sei opzioni in un dado a sei facce. Questo equivale a ⅙, o 17% (in decimali è 0,1666). È lo stesso per il lancio di un sei la seconda volta.
Utilizzando queste informazioni, possiamo determinare che la probabilità congiunta di tirare un sei la prima e la seconda volta sarà la seguente:
P(0.1666 x 0.1666) = 0.02777 o 2.8%
Questo significa che hai il 2.8% di probabilità che entrambi gli eventi accadano.
Quando usare la probabilità congiunta
La probabilità congiunta è utile quando vuoi misurare due eventi indipendenti per determinare se possono accadere contemporaneamente.
Come si usa la probabilità congiunta in relazione agli investimenti?
La probabilità congiunta è una statistica utile per analisti e statistici quando due o più fenomeni osservabili possono verificarsi simultaneamente. Per esempio, quando un declino del Dow Jones Industrial Average è accompagnato da una perdita sostanziale del valore del dollaro.
Si possono anche confrontare due azioni separate per vedere se il valore di una sale (e se lo farà anche l’altra).