
La regressione logistica è stata utilizzata nelle scienze biologiche all’inizio del ventesimo secolo. È stata poi utilizzata in molte applicazioni delle scienze sociali. La regressione logistica è usata quando la variabile dipendente (obiettivo) è categorica.
Per esempio,
- Prevedere se un’email è spam (1) o (0)
- Se il tumore è maligno (1) o no (0)
Considera uno scenario dove abbiamo bisogno di classificare se un’email è spam o no. Se usiamo la regressione lineare per questo problema, c’è bisogno di impostare una soglia in base alla quale la classificazione può essere fatta. Diciamo che se la classe effettiva è maligna, il valore continuo previsto è 0,4 e il valore di soglia è 0,5, il punto dati sarà classificato come non maligno, il che può portare a gravi conseguenze in tempo reale.
Da questo esempio, si può dedurre che la regressione lineare non è adatta al problema della classificazione. La regressione lineare non ha limiti, e questo porta la regressione logistica nel quadro. Il loro valore varia strettamente da 0 a 1.
Regressione logistica semplice
(Codice sorgente completo: https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb)
Modello
Output = 0 o 1
Ipotesi => Z = WX + B
hΘ(x) = sigmoide (Z)
Sigmoide Funzione

Se ‘Z’ va all’infinito, Y(predetto) diventa 1 e se ‘Z’ va all’infinito negativo, Y(predetto) diventa 0.
Analisi dell’ipotesi
L’output dell’ipotesi è la probabilità stimata. Questo è usato per dedurre con quanta fiducia il valore predetto può essere il valore reale quando viene dato un input X. Consideriamo l’esempio seguente,
X = =
Sulla base del valore x1, diciamo che abbiamo ottenuto la probabilità stimata di 0.8. Questo dice che c’è l’80% di possibilità che un’email sia spam.
Matematicamente questo può essere scritto come,

Questo giustifica il nome “regressione logistica”. I dati vengono inseriti in un modello di regressione lineare, che poi viene agito da una funzione logistica che predice la variabile dipendente categorica di destinazione.
Tipi di regressione logistica
1. Regressione logistica binaria
La risposta categorica ha solo due 2 possibili risultati. Esempio: Spam o No
2. Regressione logistica multinomiale
Tre o più categorie senza ordine. Esempio: Predire quale cibo è preferito di più (Veg, Non-Veg, Vegan)
3. Regressione logistica ordinale
Tre o più categorie con ordinamento. Esempio: Valutazione di un film da 1 a 5
Limite di decisione
Per prevedere a quale classe appartiene un dato, si può impostare una soglia. Sulla base di questa soglia, la probabilità stimata ottenuta è classificata in classi.
Ad esempio, se valore_previsto ≥ 0.5, allora si classifica l’email come spam altrimenti come non spam.
Il confine di decisione può essere lineare o non lineare. L’ordine polinomiale può essere aumentato per ottenere un confine decisionale complesso.
Funzione di costo
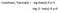
Perché la funzione di costo che è stata usata per la lineare non può essere usata per la logistica?
La regressione lineare usa l’errore quadratico medio come funzione di costo. Se questa viene usata per la regressione logistica, allora sarà una funzione non convessa dei parametri (theta). La discesa del gradiente convergerà nel minimo globale solo se la funzione è convessa.

Spiegazione della funzione di costo


Funzione di costo semplificata

Perché questa funzione di costo?
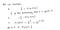
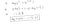
Questa funzione negativa è perché quando ci alleniamo, abbiamo bisogno di massimizzare la probabilità minimizzando la funzione di perdita. Diminuendo il costo aumenterà la massima verosimiglianza assumendo che i campioni siano tratti da una distribuzione identicamente indipendente.
Derivare la formula per l’algoritmo Gradient Descent


Implementazione Python
def weightInitialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w,bdef sigmoid_activation(result):
final_result = 1/(1+np.exp(-result))
return final_result
def model_optimize(w, b, X, Y):
m = X.shape
#Prediction
final_result = sigmoid_activation(np.dot(w,X.T)+b)
Y_T = Y.T
cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result)))))
#
#Gradient calculation
dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T))
db = (1/m)*(np.sum(final_result-Y.T))
grads = {"dw": dw, "db": db}
return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations):
costs =
for i in range(no_iterations):
#
grads, cost = model_optimize(w,b,X,Y)
#
dw = grads
db = grads
#weight update
w = w - (learning_rate * (dw.T))
b = b - (learning_rate * db)
#
if (i % 100 == 0):
costs.append(cost)
#print("Cost after %i iteration is %f" %(i, cost))
#final parameters
coeff = {"w": w, "b": b}
gradient = {"dw": dw, "db": db}
return coeff, gradient, costsdef predict(final_pred, m):
y_pred = np.zeros((1,m))
for i in range(final_pred.shape):
if final_pred > 0.5:
y_pred = 1
return y_pred
Costo vs Numero_di_Iterazioni

L’accuratezza di allenamento e test del sistema è del 100%
Questa implementazione è per la regressione logistica binaria. Per dati con più di 2 classi, deve essere usata la regressione softmax.
Questo è un post educativo e ispirato dal corso di deep learning del Prof. Andrew Ng.
Codice completo : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb