Meccanica dei Materiali
Shear Stress Equations and Applications
Sollecitazione di taglio generale:
La formula per calcolare la tensione media di taglio è:
dove τ = la sollecitazione di taglio; F = la forza applicata; A = l’area della sezione trasversale del materiale con area perpendicolare al vettore della forza applicata;
Sollecitazione di taglio della trave:
La sollecitazione di taglio della trave è definita come la sollecitazione di taglio interna di una trave causata dalla forza di taglio applicata alla trave stessa.
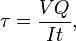dove V = forza di taglio totale nel punto in questione; Q = momento statico dell’area; t = spessore nel materiale perpendicolare al taglio; I = momento d’inerzia dell’intera sezione trasversale. Questa formula è anche conosciuta come formula di Jourawski.Semi-monocoque shearShear stress all’interno di una struttura semi-monoscocca può essere calcolato idealizzando la sezione trasversale della struttura in un insieme di traversi (portando solo carichi assiali) e webs (portando solo flussi di taglio). Dividendo il flusso di taglio per lo spessore di una data porzione della struttura semi-monoscocca si ottiene la sollecitazione di taglio. Così, la massima sollecitazione di taglio si verificherà o nell’anima di massimo flusso di taglio o di minimo spessore. Anche le costruzioni nel suolo possono fallire a causa del taglio; per esempio, il peso di una diga o di un argine riempito di terra può causare il collasso del sottosuolo, come una piccola frana.Taglio da impattoLa massima sollecitazione di taglio creata in una barra rotonda solida soggetta a impatto è data dall’equazione:
dove U = variazione di energia cinetica; G = modulo di taglio; V = volume della barra; e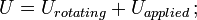 
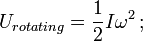
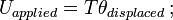
= momento di inerzia di massa; ω = velocità angolare.
Sollecitazione di taglio nei fluidi:
Qualunque fluido reale (liquidi e gas inclusi) che si muova lungo un confine solido subirà una sollecitazione di taglio su quel confine. La condizione di non scorrimento impone che la velocità del fluido al confine (relativa al confine) sia zero, ma ad una certa altezza dal confine la velocità del flusso deve essere uguale a quella del fluido. La regione tra questi due punti è giustamente chiamata strato limite. Per tutti i fluidi newtoniani in flusso laminare lo sforzo di taglio è proporzionale al tasso di deformazione nel fluido dove la viscosità è la costante di proporzionalità. Tuttavia, per i fluidi non newtoniani, questo non è più il caso poiché per questi fluidi la viscosità non è costante. Lo sforzo di taglio è impartito sul confine come risultato di questa perdita di velocità. La tensione di taglio, per un fluido newtoniano, in un elemento di superficie parallelo a una piastra piana, nel punto y, è data da:
dove μ è la viscosità dinamica del fluido; u è la velocità del fluido lungo il confine; y è l’altezza sopra il confine. In particolare, lo sforzo di taglio sulla parete è definito come: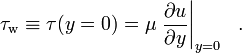 
In caso di vento, lo stress di taglio al confine è chiamato stress da vento.
1. Timoshenko, Stephen P. (1983), Storia della forza dei materiali, Courier Dover Publications, p. 141, ISBN 0486611876, http://books.google.com/?id=tkScQmyhsb8C .
2. Day, Michael A. (2004), The no-slip condition of fluid dynamics, Springer Netherlands, pp. 285-296, ISSN (Print) 1572-8420 (Online) 0165-0106 (Print) 1572-8420 (Online), http://www.springerlink.com/content/k1m4t1p02m778u88/.
3. Naqwi, A. A.; Reynolds, W. C. (jan 1987), “Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow”, NASA STI/Recon Technical Report N 87
4. Große, S.; Schröder, W. (2009), “Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars”, AIAA Journal 47 (2): 314-321, Bibcode 2009AIAAJ..47..314G, doi:10.2514/1.36892
5. Große, S.; Schröder, W. (2008), “Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³”, International Journal of Heat and Fluid Flow 29 (3): 830-840, doi:10.1016/j.ijheatfluidflow.2008.01.008