Ci sono diversi tipi di singolarità, ognuna con diverse caratteristiche fisiche che hanno caratteristiche rilevanti per le teorie da cui sono originariamente emerse, come la diversa forma delle singolarità, conica e curva. Si è anche ipotizzato che si verifichino senza Orizzonti degli Eventi, strutture che delineano una sezione di spaziotempo da un’altra in cui gli eventi non possono influire oltre l’orizzonte; questi sono chiamati nudi.
Conica
Una singolarità conica si verifica quando c’è un punto in cui il limite di ogni quantità invariante del diffeomorfismo è finito, nel qual caso lo spaziotempo non è liscio nel punto del limite stesso. Così, lo spaziotempo si presenta come un cono intorno a questo punto, dove la singolarità si trova sulla punta del cono. La metrica può essere finita ovunque il sistema di coordinate sia usato.
Un esempio di tale singolarità conica è una stringa cosmica e un buco nero di Schwarzschild.
CurvatureEdit
Le soluzioni alle equazioni della relatività generale o di un’altra teoria della gravità (come la supergravità) portano spesso a incontrare punti in cui la metrica esplode all’infinito. Tuttavia, molti di questi punti sono completamente regolari, e gli infiniti sono semplicemente il risultato dell’uso di un sistema di coordinate inappropriato in questo punto. Per verificare se c’è una singolarità in un certo punto, bisogna controllare se in questo punto le quantità invarianti al diffeomorfismo (cioè gli scalari) diventano infinite. Tali quantità sono le stesse in ogni sistema di coordinate, quindi questi infiniti non “andranno via” con un cambio di coordinate.
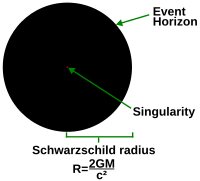
Un esempio è la soluzione di Schwarzschild che descrive un buco nero non rotante e senza carica. Nei sistemi di coordinate convenienti per lavorare in regioni lontane dal buco nero, una parte della metrica diventa infinita all’orizzonte degli eventi. Tuttavia, lo spaziotempo all’orizzonte degli eventi è regolare. La regolarità diventa evidente quando si passa ad un altro sistema di coordinate (come le coordinate di Kruskal), dove la metrica è perfettamente liscia. D’altra parte, al centro del buco nero, dove anche la metrica diventa infinita, le soluzioni suggeriscono l’esistenza di una singolarità. L’esistenza della singolarità può essere verificata notando che lo scalare di Kretschmann, essendo il quadrato del tensore di Riemann, cioè R μ ν ρ σ R μ ν ρ σ {displaystyle R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }}

, che è invariante al diffeomorfismo, è infinito.
Mentre in un buco nero non rotante la singolarità si verifica in un singolo punto nelle coordinate del modello, chiamato “singolarità puntiforme”, in un buco nero rotante, noto anche come buco nero di Kerr, la singolarità si verifica su un anello (una linea circolare), noto come “singolarità anulare”. Una tale singolarità può anche diventare teoricamente un wormhole.
Più in generale, uno spaziotempo è considerato singolare se è geodeticamente incompleto, il che significa che ci sono particelle in caduta libera il cui moto non può essere determinato oltre un tempo finito, essendo dopo il punto di raggiungimento della singolarità. Per esempio, qualsiasi osservatore all’interno dell’orizzonte degli eventi di un buco nero non rotante cadrebbe nel suo centro entro un periodo di tempo finito. La versione classica del modello cosmologico del Big Bang dell’universo contiene una singolarità causale all’inizio del tempo (t=0), dove tutte le geodetiche del tempo non hanno estensioni nel passato. Estrapolando all’indietro a questo ipotetico tempo 0 si ottiene un universo con tutte le dimensioni spaziali di dimensione zero, densità infinita, temperatura infinita e curvatura spaziale infinita.
Singolarità nudaModifica
Fino ai primi anni ’90, era opinione diffusa che la relatività generale nascondesse ogni singolarità dietro un orizzonte degli eventi, rendendo impossibile le singolarità nude. Questo è indicato come l’ipotesi della censura cosmica. Tuttavia, nel 1991, i fisici Stuart Shapiro e Saul Teukolsky hanno eseguito simulazioni al computer di un piano rotante di polvere che indicavano che la relatività generale potrebbe consentire singolarità “nude”. Non si sa quale sarebbe l’aspetto di questi oggetti in un tale modello. Né si sa se le singolarità sorgerebbero ancora se le ipotesi semplificatrici usate per fare la simulazione fossero rimosse. Tuttavia, si ipotizza che la luce che entra in una singolarità avrebbe analogamente le sue geodetiche terminate, facendo così apparire la singolarità nuda come un buco nero.
Gli orizzonti degli eventi che scompaiono esistono nella metrica di Kerr, che è un buco nero che gira nel vuoto, se il momento angolare ( J {displaystyle J}

) è abbastanza alto. Trasformando la metrica di Kerr in coordinate di Boyer-Lindquist, si può dimostrare che la coordinata (che non è il raggio) dell’orizzonte degli eventi è, r ± = μ ± ( μ 2 – a 2 ) 1 / 2 {\displaystyle r_{\pm }=\mu \pm (\mu ^{2}-a^{2})^{1/2}

, dove μ = G M / c 2 {displaystyle \mu =GM/c^{2}}

, e a = J / M c {\displaystyle a=J/Mc}

. In questo caso, “gli orizzonti degli eventi scompaiono” significa quando le soluzioni sono complesse per r ± {displaystyle r_{\pm }}

, oppure μ 2 < a 2 {displaystyle \mu ^{2}<a^{2}

. Tuttavia, questo corrisponde ad un caso in cui J {\displaystyle J}

supera G M 2 / c {\displaystyle GM^{2}/c}

(o in unità Planck, J > M 2 {displaystyle J>M^{2}}

), cioè lo spin supera quello che è normalmente visto come il limite superiore dei suoi valori fisicamente possibili.
Similmente, la scomparsa degli orizzonti degli eventi può essere vista anche con la geometria di Reissner-Nordström di un buco nero carico se la carica ( Q {displaystyle Q}

) è abbastanza alta. In questa metrica, si può dimostrare che le singolarità si verificano a r ± = μ ± ( μ 2 – q 2 ) 1 / 2 {\displaystyle r_{\pm }=\mu \pm (\mu ^{2}-q^{2})^{1/2}

, dove μ = G M / c 2 {displaystyle \mu =GM/c^{2}}


. Dei tre casi possibili per i valori relativi di μ {displaystyle \mu }

e q {displaystyle q}

, il caso in cui μ 2 < q 2 {displaystyle \mu ^{2}<q^{2}

provoca sia r ± {displaystyle r_{\pm}

siano complessi. Questo significa che la metrica è regolare per tutti i valori positivi di r {\displaystyle r}

, o in altre parole, la singolarità non ha orizzonte degli eventi. Tuttavia, questo corrisponde a un caso in cui Q / 4 π ϵ 0 {displaystyle Q/{sqrt {4\pi \epsilon _{0}}}}

supera M G {displaystyle M{sqrt {G}}

(o in unità Planck, Q > M {displaystyle Q>M}

), cioè la carica supera quello che è normalmente considerato il limite superiore dei suoi valori fisicamente possibili. Inoltre, i buchi neri astrofisici reali non dovrebbero possedere alcuna carica apprezzabile.
Un buco nero che possiede il più basso M {displaystyle M}

valore coerente con il suo J {displaystyle J}

e Q {\displaystyle Q}
