Vi starete chiedendo cosa sono tutte queste somme di quadrati. Forse è quello che vi ha portato qui in primo luogo. Bene, sono i fattori determinanti di una buona regressione lineare. Questo tutorial si basa sulla struttura ANOVA che potreste aver sentito prima.
Prima di leggerlo, però, assicuratevi di non confondere la regressione con la correlazione. Se hai controllato questo, possiamo passare direttamente all’azione.
Una rapida nota a margine: vuoi imparare di più sulla regressione lineare? Guarda i nostri video esplicativi Il modello di regressione lineare. Rappresentazione geometrica e Il modello di regressione lineare semplice.
SST, SSR, SSE: definizione e formule
Ci sono tre termini che dobbiamo definire. La somma dei quadrati totali, la somma della regressione dei quadrati e la somma dell’errore dei quadrati.

Cos’è la SST?
La somma dei quadrati totali, indicata con SST, è la differenza al quadrato tra la variabile dipendente osservata e la sua media. Si può pensare a questo come alla dispersione delle variabili osservate intorno alla media – un po’ come la varianza nelle statistiche descrittive.
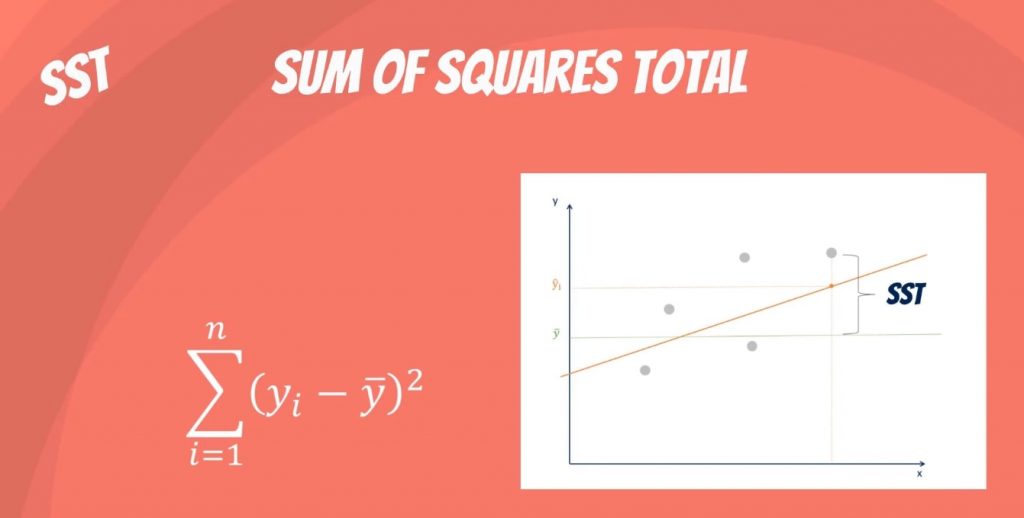
È una misura della variabilità totale del dataset.
Nota a margine: c’è un’altra notazione per la SST. È TSS o somma totale dei quadrati.
Che cos’è la SSR?
Il secondo termine è la somma dei quadrati dovuti alla regressione, o SSR. È la somma delle differenze tra il valore predetto e la media della variabile dipendente. Pensatelo come una misura che descrive quanto bene la nostra linea si adatti ai dati.

Se questo valore di SSR è uguale alla somma dei quadrati totali, significa che il nostro modello di regressione cattura tutta la variabilità osservata ed è perfetto. Ancora una volta, dobbiamo menzionare che un’altra notazione comune è ESS o somma spiegata dei quadrati.
Che cos’è l’SSE?
L’ultimo termine è l’errore della somma dei quadrati, o SSE. L’errore è la differenza tra il valore osservato e il valore previsto.

Di solito vogliamo minimizzare l’errore. Più piccolo è l’errore, migliore è il potere di stima della regressione. Infine, dovrei aggiungere che è anche conosciuto come RSS o somma residua dei quadrati. Residuo come: rimanente o inspiegabile.
La confusione tra le diverse abbreviazioni
Diventa davvero confuso perché alcune persone lo denotano come SSR. Questo rende poco chiaro se stiamo parlando della somma dei quadrati dovuti alla regressione o della somma dei residui al quadrato.

In ogni caso, nessuno dei due è universalmente adottato, quindi la confusione rimane e dovremo conviverci.
Basta ricordare che le due notazioni sono SST, SSR, SSE, o TSS, ESS, RSS.

C’è un conflitto sulle abbreviazioni, ma non sul concetto e la sua applicazione. Quindi, concentriamoci su questo.
Come sono correlati?
Matematicamente, SST = SSR + SSE.

La logica è la seguente: la variabilità totale del set di dati è uguale alla variabilità spiegata dalla linea di regressione più la variabilità non spiegata, nota come errore.

Data una variabilità totale costante, un errore inferiore causerà una regressione migliore. Al contrario, un errore più alto causerà una regressione meno potente. Ed è questo che dovete ricordare, indipendentemente dalla notazione.
Passo successivo: Il quadrato R
Bene, se non siete sicuri del perché abbiamo bisogno di tutte quelle somme di quadrati, abbiamo lo strumento giusto per voi. Il quadrato R. Volete saperne di più? Basta tuffarsi nel tutorial collegato dove capirete come misurare il potere esplicativo di una regressione lineare!
***
Interessato ad imparare di più? Puoi portare le tue competenze da buone a ottime con il nostro corso di statistica.
Prova gratuitamente il corso di statistica
Il prossimo tutorial: Misurare la variabilità con il quadrato R