La trasformata di Fourier (FT) decompone un segnale nelle frequenze che lo compongono.
Cosa significa? Abbiamo un segnale S1.

Se vogliamo misurare la forza di questo segnale in un momento specifico. Lo misuriamo dalla sua ampiezza.
Quindi, l’ampiezza del segnale S1 è 1
Se facciamo lo stesso per un altro segnale e selezioniamo lo stesso momento nel tempo e misuriamo la sua ampiezza. Abbiamo un altro segnale S2 come questo

Anche l’ampiezza del segnale S2 è 2
Ora, cosa succede quando emettiamo questi due segnali contemporaneamente (S1 e S2) ?
Quindi, quando emettiamo questi due segnali nello stesso istante di tempo, otteniamo un nuovo segnale che è la somma dell’ampiezza di questi due segnali. È così perché questi due segnali vengono sommati.

Quindi, l’ampiezza di S3 = ampiezza di S1 + ampiezza di S2 = 1 + 2 = 3
Quindi, l’ampiezza del segnale S3 è 3
Ora, la domanda interessante è :
Se ci viene dato solo il segnale S3 (che è la somma dei segnali S1 e S2).Possiamo recuperare i segnali originali S1 e S2?
Sì. Questo è ciò che fa una trasformata di Fourier. Prende un segnale e lo decompone alle frequenze che lo compongono.
Nel nostro esempio, una trasformata di Fourier decomporrebbe il segnale S3 nelle sue frequenze costituenti come i segnali S1 e S2
Ma, come possiamo recuperare i segnali originali? Cosa farà la trasformata di Fourier per noi?

Lasciamo che i tre segnali nella figura precedente siano S1, S2, e S3 e quando uniamo questi tre segnali insieme otteniamo il segnale in rosso che è in realtà la somma dei tre segnali S1+S2+S3.
Quello che fa la trasformata di Fourier è che ci sposta dal dominio del tempo al dominio della frequenza.
In caso, se qualcuno si sta chiedendo, cosa succede se vogliamo tornare dal dominio della frequenza al dominio del tempo? Ma non ne parleremo in questo articolo.
Generazione del segnale e spostamento di fase
Se vogliamo descrivere un segnale, abbiamo bisogno di tre cose :
- La frequenza del segnale che mostra, quante occorrenze nel periodo abbiamo.
- Ampiezza che mostra l’altezza del segnale o in altri termini la forza del segnale.
- Spostamento di fase come dove inizia il segnale.
Il primo esempio che abbiamo preso era molto semplice, ogni segnale aveva la stessa frequenza e differenza di fase e solo diverse ampiezze.
Ora guarderemo un esempio leggermente complesso e guarderemo il singolo segnale dell’esempio precedente perché per capire meglio la trasformata di Fourier dobbiamo guardare i singoli segnali da vicino.
Di seguito i segnali originali che stavamo guardando sopra.



Frequenza: Se guardiamo da vicino i tre segnali, noteremo che la frequenza di tutti e tre i segnali è diversa.
Se per lo stesso periodo di tempo, nel segnale 1 c’è n numero di onde allora ci sono 2n numero di onde nel segnale 2 e viceversa.
Fase: Inoltre, quando guardiamo da vicino dove inizia effettivamente il segnale. Troveremo che mentre il segnale 1 inizia a (0,0), il segnale 2 inizia a (-0,5,0) se tracciamo l’onda per incontrare l’asse y a 0. Quindi, a 0 abbiamo già la massima ampiezza del segnale. Questo è ciò che chiamiamo spostamento di fase.
Ampiezza: Tutti e tre i segnali hanno ampiezze diverse, il segnale 1 ha un’ampiezza di 1 mentre il segnale 2 e il segnale 3 hanno un’ampiezza di 2 e 3 rispettivamente.
Tutto questo è catturato in una formula matematica elegante e super semplice. Quindi, negli esempi di cui sopra, se l’asse x è definito come x e l’asse y è definito come y. Possiamo generare y come funzione di t tale che :

Usando questa formula, possiamo generare qualsiasi tipo di segnale che vogliamo e poi possiamo unirli insieme e giocare con loro. Per esempio, se uniamo i segnali 1, 2 e 3. otterremo un segnale come questo:

La matematica dietro la trasformata di Fourier
L’idea principale dietro la trasformata di Fourier è che :
Ogni segnale continuo nel dominio del tempo può essere rappresentato univocamente e senza ambiguità da una serie infinita di sinusoidi.
Cosa significa questo?
Significa che, se abbiamo un segnale e questo segnale è generato da qualche funzione x(t) allora possiamo trovare un’altra funzione f(t) tale che :

Quindi, Non importa quanto sia forte il segnale, possiamo trovare una funzione come f(t) che è una somma di una serie infinita di sinusoidi che rappresenterà effettivamente il segnale perfettamente.
Ora, la domanda che sorge è: come facciamo a trovare i coefficienti qui nell’equazione di cui sopra, perché questi sono i valori che determinano la forma dell’uscita e quindi il segnale.
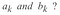
Quindi, per ottenere questi coefficienti usiamo la trasformata di Fourier e il risultato della trasformata di Fourier è un gruppo di coefficienti. Quindi, usiamo X(F) per indicare i coefficienti di Fourier ed è una funzione di frequenza che si ottiene risolvendo l’integrale tale che :
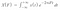
La parte difficile in questo integrale è in realtà il i che denota un numero complesso. Quindi, probabilmente ricordiamo che i² = -1 o i = √-1. Potrebbe anche aiutare a ricordare che la forma di un numero complesso è a + ib . Quindi, ha una parte reale e una immaginaria.
Inoltre, quando risolviamo effettivamente l’integrale di cui sopra, otteniamo questi numeri complessi dove a e b corrispondono ai coefficienti che stiamo cercando.
Abbiamo però tre problemi che dobbiamo affrontare :
- Come affrontare
i. - Come trattare i segnali discreti.
Perciò, iniziamo con il secondo.
Per capire la trasformata discreta di Fourier, dobbiamo prima capire come campionare un segnale continuo?
Secondo Wikipedia, Nell’elaborazione dei segnali, il campionamento è la riduzione di un segnale a tempo continuo a un segnale a tempo discreto. Ecco un esempio di come la forma del segnale cambia con il cambiamento della frequenza di campionamento :
Lasciamo che il segnale originale sia un segnale con un’ampiezza di due e una frequenza di cinque su un periodo di un secondo:
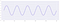
Ora, diminuendo la frequenza di campionamento, guardiamo come cambia la forma del segnale:
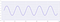
Man mano che diminuiamo la frequenza di campionamento otteniamo :

Quindi, la linea di fondo è : Più alta è la frequenza di campionamento, migliore è la qualità del segnale e inoltre possiamo distinguere tra più frequenze.
Ora che sappiamo come campionare i segnali, guarderemo la modifica degli algoritmi conosciuti come Trasformata Discreta di Fourier.
Trasformata discreta di Fourier
Ogni segnale campionato di lunghezza N nel dominio del tempo può essere rappresentato univocamente e senza ambiguità da una serie finita di sinusoidi.
Quindi, non abbiamo più a che fare con l’infinito nella nostra nuova definizione.
Qual è la differenza?
Nella trasformata di Fourier standard, abbiamo usato una funzione del tempo x(t) per generare un segnale continuo. Ora, nel caso discreto, non abbiamo una funzione, abbiamo un set di dati, un insieme di punti che otteniamo campionando il segnale continuo. Quindi, userò {x} per donare un dataset tale che contenga la lettura del campionamento tale che :

e quello che la Trasformata Discreta di Fourier Transform farà per noi è che trasformerà il dataset di {x} in un altro dataset {X} che conterrà i coefficienti di Fourier tali che :

Se guardiamo la definizione di trasformata di Fourier, ogni X in {X} è un numero complesso e contiene le a e b componenti delle frequenze.
Ma come mai i due dataset {x} e {X} hanno la stessa lunghezza?
Se pensiamo, ciò che guida la lunghezza del {x} dataset è la frequenza di campionamento perché, in un periodo di tempo, il numero di punti dati che leggo è esattamente la frequenza di campionamento giusto? Se pensiamo all’altro dataset {X} , abbiamo detto che la frequenza è il numero di occorrenze per unità di tempo. Quindi, se sto campionando con una certa frequenza, non posso riconoscere i segnali che hanno una frequenza maggiore della frequenza di campionamento solo perché non abbiamo abbastanza punti dati.
Quindi, se abbiamo segnali con frequenze molto alte su una frequenza di campionamento molto bassa, non saremo in grado di riconoscere questi segnali. Quindi, il numero di frequenze che possiamo riconoscere applicando la trasformata di Fourier è in realtà guidato anche dalla frequenza di campionamento.
Quindi, ora che abbiamo il nostro dataset {x} otterremo {Xk} tale che è un elemento in {X} che sono i miei coefficienti di Fourier tali che :
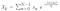
Dunque, questa è essenzialmente la trasformata discreta di Fourier. Possiamo fare questo calcolo e produrrà un numero complesso nella forma di a + ib dove abbiamo due coefficienti per la serie di Fourier.
Ora, sappiamo come campionare i segnali e come applicare una Trasformata Discreta di Fourier. L’ultima cosa che vorremmo fare è sbarazzarci del numero complesso i perché non è supportato in mllib o systemML utilizzando qualcosa conosciuto come formula di Eulero che afferma :
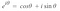
Quindi, Se inseriamo la formula di Eulero nell’equazione della trasformata di Fourier, otteniamo

sappiamo anche che cos(-θ) = cos(θ) e sin(-θ) = -sin(θ) e se usiamo questo nell’equazione di cui sopra, l’equazione potrebbe essere semplificata come :

e possiamo effettivamente spezzare l’equazione di cui sopra in due somme in modo tale che :

ora, Se confrontiamo l’equazione di cui sopra con l’equazione di un numero complesso che è a + ib allora otteniamo il valore corrispondente come :
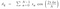
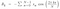
Quindi, ora possiamo mettere questi valori nell’equazione di f(t) e ottenere il risultato.
Conclusione
In pratica usiamo una leggera modifica della trasformata discreta di Fourier conosciuta come trasformata veloce di Fourier perché la trasformata discreta di Fourier è molto semplice, basilare e anche lenta. Non è adatta allo scopo se vogliamo davvero fare qualcosa in ambiente di produzione. La complessità di calcolo della Trasformata discreta di Fourier è quadratica O(n²) e la Trasformata veloce di Fourier per confronto è quasi lineare O(nlogn). La Fast Fourier Transform fa questo sfruttando l’assimetria nella trasformazione di Fourier.