統計学の定義 >
リッカート尺度とは?
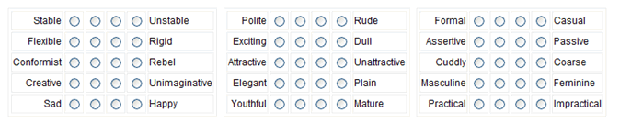
リッカート尺度のバリエーション
リッカート尺度とは、態度や意見を測定するための評価尺度の一種です。 この尺度では、回答者は項目を同意のレベルで評価するよう求められます。 例:
- 大賛成
- 賛成
- どちらともいえない
- 反対
- 大反対
通常、5~7項目が尺度に使用されます。 尺度は「賛成」「反対」だけではなく、「賛成」「頻度」「質」「重要性」などのテーマで数十のバリエーションが可能です。 例えば:
- 同意。
- 同意:強く同意する~強く同意しない。
- 頻度:頻繁にある~全くない。
- 頻度:「よくある」から「まったくない」まで。
- Likelihood(可能性):非常に良いから非常に悪い。
- 重要性:「非常に重要」から「重要ではない」まで。
これらの項目をリッカート尺度の回答アンカーと呼びます。
回答者が答えた後、その回答に番号を付けます。 例えば、
大賛成=5
賛成=4
どちらでもない=3
反対=2
大反対=1
これにより、回答に意味を持たせることができます。 例えば、カスタマーサービスに関するアンケートでは、どのカスタマーサービス担当者が良いサービスを提供しているか (平均スコアが 4-5) 、どの担当者が悪いサービスを提供しているか (平均スコアが 1-2) を知ることができます。
リッカート尺度を開発するためのステップ
- 焦点を定義する:測定しようとしているのは何か? トピックは一次元でなければなりません。 たとえば、「カスタマーサービス」や「このウェブサイト」などです。
- リッカート尺度の項目を作成します。 項目は、何らかの尺度で評価できるものでなければなりません。 このページのトップにある画像には、いくつかの提案があります。 たとえば、礼儀正しさ/無礼さは、”非常に礼儀正しい”、”礼儀正しい”、”礼儀正しくない”、”非常に無礼である “と評価できます。
- リッカート尺度の項目を評価してください。 焦点が合っているかどうかを確認したいので、何人かのチームを選んで、上記ステップ2の項目を見て、焦点に対して好ましい/中立/好ましくないと評価してもらいます。
- リッカート尺度テストの実施
リッカート尺度の仮説検定
リッカート尺度データの分析を行うことがわかっている場合、データを収集してから分析について決定するのではなく、開発段階で質問を調整するほうが簡単です。
リッカート尺度のデータに対して、t 検定のようなパラメトリックな検定を行うべきか、Mann-Whitney のようなノンパラメトリックな仮説検定を行うべきかについては、教育や研究の現場でも意見が分かれています。
「結論として、t 検定と一般的に同等の検出力を持ちますが、歪んだ分布、尖った分布、多峰性の分布については、2 つの検定の間に強い検出力の差が生じます。
つまり、歪んだ分布、尖った分布、多峰性の分布を除き、パラメトリック検定とノンパラメトリック検定の結果に実質的な違いはないようです。 どのような方法を取るかは、あなたやあなたの部署、そしておそらく投稿先のジャーナル(もしあれば)次第です。 決断の段階で最も重要なステップは、データを順序データと区間データのどちらで扱うかを決めることです。 そして、以下のデータタイプのセクションを読んでください。
- リッカート尺度で回答する一連の質問については、データを順序変数として扱います。
- 単一の構成要素 (性格特性や態度) を記述する一連のリッカート尺度の質問については、データを間隔変数として扱います。
2つのオプション
ほとんどのリッカート尺度は順序変数に分類されます。 変数間の距離が一定であることが100%確実な場合は、テスト目的で間隔変数として扱うことができます。 ほとんどの場合、データは順序変数になります。例えば、「強く同意する」と「同意する」、「同意する」と「どちらでもない」の違いを見分けることは不可能だからです。
Ordinal Scale Data
ほとんどの変数タイプ (interval、ratio、nominal) では、平均を求めることができます。 しかし、リッカート尺度データには当てはまりません。 リッカート尺度では、データ項目間の「距離」がわからないため、平均を求めることができません。 つまり、1,2,3の平均を求めることはできても、”賛成”、”反対”、”どちらでもない “の平均を求めることはできません。
「『まあまあ』と『良い』の平均は『まあまあ』ではない。 – Susan Jamieson paraphrasing Kuzon Jr et al. (Jamieson, 2004)
Statistics Choices
使用できる統計は以下の通りです。
仮説検証
リッカート尺度の仮説検証では、独立変数はグループを、従属変数は測定対象の構成要素を表します。 たとえば、思いやりのレベルを測定するために看護学生を調査する場合、独立変数は看護学生のグループで、従属変数は思いやりのレベルです。
実行可能なテストの種類:
- Kruskal Wallis: 2つのグループの中央値が異なるかどうかを判断する。
- Mann Whitney U 検定: 2つのグループの中央値が異なるかどうかを判断する。 単一のリッカート尺度の質問を評価するのは簡単ですが、中心傾向バイアス、黙認バイアス、社会的望ましさバイアスなど、いくつかのバイアスに悩まされます。
2つのカテゴリーでより多くの選択肢
回答を、例えば「賛成」と「反対」のように2つのカテゴリーにまとめると、より多くのテストの選択肢が開けます。
- カイ二乗。 この検定は、結果がカテゴリーに入れられたカウントである多項実験用に設計されています。
- McNemar 検定。
- McNemar 検定: カテゴリに対する応答が 2 つのグループ/条件で同じであるかどうかを検定します。
- Cochran’s Q 検定。
- Friedman 検定: 複数の試行における治療法の違いを見つけるための検定。
Measures of Association
あるリッカート尺度の項目に対して、あるグループの人々が他のグループの人々と異なる回答(高いまたは低い)をしているかどうかを知りたい場合があります。 この質問に答えるには、(上に挙げたような) 差の検定ではなく、関連性の尺度を使用します。
年齢グループのように、グループが何らかの方法で順序付けられている場合は、以下のように使用することができます。
- Kendallのタウ係数またはタウの変種 (例えば、ガンマ係数、SomersのD)。
- スピアマン順位相関
グループが順序的でない場合は、以下のいずれかを使用します:
- ファイ係数
- コンティンジェンシー係数
- クラーマーのV。
インターバルスケールデータ
インターバルスケールのリッカート尺度データに適した統計:
- 平均値。
- 標準偏差
インターバルスケールのリッカートデータに適した仮説検定:
- T-テスト
- ANOVA
- 回帰分析(順序付きロジスティック回帰または多項ロジスティック回帰のいずれか)。
——————————————————————————
宿題やテストの問題で助けが必要ですか? Chegg Studyでは、その分野の専門家からステップバイステップで質問に対する解決策を得ることができます。 Cheggチューターとの最初の30分は無料です。