
ロジスティック回帰は、20世紀初頭に生物科学の分野で使用されました。 その後、多くの社会科学の分野で使われるようになりました。
例えば、
- 電子メールがスパムであるかどうかを予測する(1)または(0)
- 腫瘍が悪性であるかどうか(1)または(0)
電子メールがスパムであるかどうかを分類する必要があるシナリオを考えてみましょう。 この問題に線形回帰を使用する場合、分類を行うことができるしきい値を設定する必要があります。 例えば、実際のクラスが悪性で、予測連続値が0.4、閾値が0.5の場合、データポイントは悪性ではないと分類されますが、これはリアルタイムで深刻な結果につながる可能性があります。
この例から、線形回帰は分類問題には適していないと推測できます。
この例から、線形回帰が分類問題に適していないことが推測できます。線形回帰は境界がないため、ロジスティック回帰が登場します。 その値は厳密には0から1の範囲です。
シンプルなロジスティック回帰
(全ソースコード。 https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb)
モデル
出力=0または1
仮説=> Z = WX + B
hΘ(x)=sigmoid (Z)
Sigmoid 関数

‘Z’が無限大になれば、Y(predified)は1になり、’Z’が負の無限大になれば、Y(predified)は0になります。
仮説の分析
仮説の出力は、推定確率です。 これは、入力Xが与えられたときに、予測値が実際の値になる確率を推測するために使用されます。 これは、電子メールがスパムである確率が80%であることを意味します。
数学的には次のように書くことができます。

これで「ロジスティック回帰」という名前が正当化されました。
ロジスティック回帰の種類
1. 2値ロジスティック回帰
カテゴリー別の回答には2つの可能な結果があります。 例 スパムか否か
2.多項ロジスティック回帰
順序付けされていない3つ以上のカテゴリーがある。 例。 どの食べ物がより好まれるかを予測する(Veg, Non-Veg, Vegan)
3.順序ロジスティック回帰
3つ以上のカテゴリーで順序付けがあるもの。 例。
Decision Boundary
あるデータがどのクラスに属するかを予測するために、閾値を設定することができます。
予測値が0.5以上であれば、メールをスパムとして分類し、そうでなければスパムではないと分類することができます。 多項式の次数を増やすことで、複雑な決定境界を得ることができます。
コスト関数
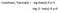
なぜ、線形で使われていたコスト関数がロジスティックでは使えないのか?
線形回帰では、平均二乗誤差をコスト関数として使用します。 これをロジスティック回帰に使用すると、パラメータ(θ)の非凸関数となります。 勾配降下法は、関数が凸である場合にのみグローバル・ミニマムに収束します。

コスト関数の説明
div

。

単純化されたコスト関数

なぜこのコスト関数なのか?
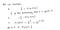
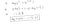
この負の関数は、トレーニングをするときに、損失関数を最小にして確率を最大にする必要があるからです。 コストを減少させることで、サンプルが同一の独立した分布から引き出されると仮定した場合、最大尤度が増加します。
Gradient Descent Algorithmの計算式の導出

。

Pythonでの実装
def weightInitialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w,bdef sigmoid_activation(result):
final_result = 1/(1+np.exp(-result))
return final_result
def model_optimize(w, b, X, Y):
m = X.shape
#Prediction
final_result = sigmoid_activation(np.dot(w,X.T)+b)
Y_T = Y.T
cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result)))))
#
#Gradient calculation
dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T))
db = (1/m)*(np.sum(final_result-Y.T))
grads = {"dw": dw, "db": db}
return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations):
costs =
for i in range(no_iterations):
#
grads, cost = model_optimize(w,b,X,Y)
#
dw = grads
db = grads
#weight update
w = w - (learning_rate * (dw.T))
b = b - (learning_rate * db)
#
if (i % 100 == 0):
costs.append(cost)
#print("Cost after %i iteration is %f" %(i, cost))
#final parameters
coeff = {"w": w, "b": b}
gradient = {"dw": dw, "db": db}
return coeff, gradient, costsdef predict(final_pred, m):
y_pred = np.zeros((1,m))
for i in range(final_pred.shape):
if final_pred > 0.5:
y_pred = 1
return y_pred
コストと反復回数の関係p

システムのトレーニングとテストの精度は100%
この実装は、バイナリロジスティック回帰のためのものです。
これは教育的な投稿であり、Andrew Ng教授の深層学習コースからヒントを得ています。
Full code : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb