材料力学
剪断応力の式と応用
一般的な剪断応力：
平均的な剪断応力を計算する式は次のとおりです。
ここでτ=せん断応力、F=加えられた力、A=加えられた力ベクトルに垂直な面積を持つ材料の断面積
梁のせん断:
梁のせん断は、梁に加えられたせん断力によって生じる梁の内部せん断応力と定義されます。
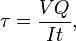ここで、V = 当該位置での全せん断力、Q = 面積の静力学的モーメント、t = せん断に垂直な材料の厚さ、I = 断面積全体の慣性モーメント。 セミモノコックのせん断セミモノコック構造内のせん断応力は、構造体の断面をストリンガー（軸方向の荷重のみを受ける）とウェブ（せん断流のみを受ける）のセットに理想化することで計算できます。 せん断流をセミモノコック構造の所定の部分の厚さで割ると，せん断応力が得られる。 したがって、最大せん断応力は、最大せん断流または最小厚さのウェブのいずれかで発生することになります。 例えば、土で埋められたダムや堤防の重さで、小さな地滑りのように下層土が崩壊することがあります。衝撃せん断固体の丸棒に衝撃を与えたときに生じる最大のせん断応力は、次の式で与えられます。
ここで、U = 運動エネルギーの変化、G = せん断弾性率、V = 棒の体積。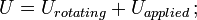 
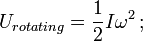
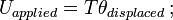
= 質量慣性モーメント; ω=角速度。
流体のせん断応力:
固体の境界に沿って移動する実在の流体 (液体と気体を含む) は、その境界にせん断応力を発生させます。 滑り止め条件では、境界での流体の速度 (境界に対する相対的な速度) はゼロですが、境界からある高さでは、流れの速度が流体の速度と等しくなければなりません。 この2つの点の間の領域を境界層と呼びます。 層流のすべてのニュートン流体では、せん断応力は、粘度を比例定数とする流体のひずみ速度に比例します。 しかし、非ニュートン流体の場合は、粘度が一定ではないため、これはもはや当てはまりません。 剪断応力は、この速度低下の結果、境界に与えられます。 ニュートン流体の場合、平板に平行な表面要素の点yでのせん断応力は次のように与えられます。
ここで、μは流体の動的粘度、uは境界に沿った流体の速度、yは境界上の高さです。 具体的には、壁せん断応力は次のように定義されます。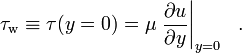 
風の場合、境界でのせん断応力を風応力と呼びます。
1. Timoshenko, Stephen P. (1983), History of Strength of Material, Courier Dover Publications, p. 141, ISBN 0486611876, http://books.google.com/?id=tkScQmyhsb8C .
2. Day, Michael A. (2004), The no-slip condition of fluid dynamics, Springer Netherlands, pp.285-296, ISSN (Print) 1572-8420 (Online) 0165-0106 (Print) 1572-8420 (Online), http://www.springerlink.com/content/k1m4t1p02m778u88/.
3. Naqwi, A. A.; Reynolds, W. C. (jan 1987), “Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow”, NASA STI/Recon Technical Report N 87
4. Große, S.; Schröder, W. (2009), “Two-Dimensional wave laser-Doppler method for measurement of skin friction in fluid flow”, NASA STI/Recon Technical Report N 87
5. (2009), “Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars”, AIAA Journal 47 (2): 314-321, Bibcode 2009AIAAJ..47…314G, doi:10.2514/1.36892
5. Große, S.; Schröder, W. (2008), “Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³”, International Journal of Heat and Fluid Flow 29 (3): 830-840, doi:10.1016/j.ijheatfluidflow.2008.01.008
。