Guinguette Marais Poitevin

依存性のある事象の扱い方

人生にはランダムな事象がたくさんあります。

独立事象

事象は「独立」することができ、各事象は他の事象の影響を受けないことを意味します。 Tossing a coin.

コインの各トスは、完全に孤立したものです。

過去に行われたことは、現在のトスには影響しません。

確率は、コインのどのトスと同様に、単純に 2 分の 1、つまり 50% です。

従って、各トスは独立事象です。

依存事象

しかし、事象は「依存」することもできます…つまり、以前の事象によって影響を受けることができます…。

これは、袋からビー玉を取り出しているからです。

このように、次のイベントは前のイベントで起こったことに依存しており、これを依存性と呼びます。

従属事象はここで見ているものです。

ツリーダイアグラム

ツリーダイアグラムは、何が起こっているのかをイメージするのに非常に優れた方法ですので、ビー玉の例で作ってみましょう。

青のビー玉を取る確率は 2/5、赤のビー玉を取る確率は 3/5 です。

さらに一歩進んで、2 つ目のビー玉を取るとどうなるかを見てみましょう。

青いビー玉が最初に選ばれた場合、青いビー玉を得る確率は1/4、赤いビー玉を得る確率は3/4です。

赤いビー玉が最初に選ばれた場合、青いビー玉を得る確率は 2/4、赤いビー玉を得る確率は 2/4 になります。

記法

数学では記法が大好きです! それは、代数の力を使ってアイデアを弄ることができるということです。

P(A)は「事象Aの確率」を意味します

ビー玉の例では、事象Aは「青いビー玉を最初に手に入れる」ことであり、その確率は2/5です:

P(A)=2/5

そして、事象Bは「青いビー玉を2番目に手に入れる」ことです…。

• 青いビー玉を先に手に入れた場合、確率は1/4になります
• 赤いビー玉を先に手に入れた場合、確率は2/4になります

だから、どちらが欲しいかを言わなければならないし、「｜」という記号は「与えられた」という意味で使います。

P(B|A)は「事象Aが与えられた事象B」を意味します

つまり、事象Aはすでに起こっていて、次に事象Bが起こる可能性は？

P(B|A)は、Aが与えられたBの「条件付き確率」とも呼ばれます。

そして、今回のケースでは、

P(B|A) = 1/4

つまり、青いビー玉を2個手に入れる確率は。

そして、次のように書きます

。

「事象Aと事象Bの確率は、
事象Aの確率×事象Aを与えられた事象Bの確率に等しい」

次の例を記法だけでやってみましょう。

隠されたデータの発見

代数を使って、次のように式の「主語を変える」こともできます：

Start with:		P(A and B) = P(A) x P(B|A)
Swap sides:		P(A) x P(B|A) = P(A and B)
P(A)で割る。		P(B|A) = P(A and B) / P(A)

そして、もう一つの便利な公式があります。

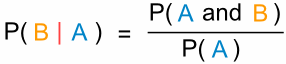
「事象Aが与えられたときの事象Bの確率は、
事象Aと事象Bの確率を事象Aの確率で割ったものに等しい」

大きな例。 サッカーゲーム

あなたはサッカーに行くことになり、ゴールキーパーになりたいと思っていますが、それは今日のコーチが誰かによります：

• サムコーチの場合、ゴールキーパーになる確率は0.5です
• アレックスコーチの場合、ゴールキーパーになる確率は0.3

サムがコーチになる頻度は、10試合に6回程度（確率は0.6）です。

では、今日、あなたがゴールキーパーになる確率はどれくらいでしょうか？

ツリーダイアグラムを作ってみましょう。 まず、2人の可能なコーチを示します。

Sam が選ばれる確率は 0.6 で、Alex が選ばれる確率は 0.4 です (合わせて 1)

さて、Sam が選ばれた場合、ゴールキーパーになる確率は 0.5 です (ゴールキーパーにならない確率は 0. 5 です)。5):

Alexを得た場合、Goalieになる確率は0.3 (そして、Goalieにならない確率は0.7):

樹形図が完成しましたので、全体の確率を計算してみましょう。

P(A and B) = P(A) x P(B|A)

ここでは、「Sam, Yes」の枝についてのやり方を説明します：

(Samがコーチになる確率0.

しかし、まだ終わっていません!

Alex がコーチである確率が 0.4 で、それに 0.3 が続くと 0.12 になります

そして、ツリーの 2 つの「はい」の枝を合わせると、次のようになります。42

(42% の確率です)

確認

最後のステップとして、計算を完了し、それらの合計が 1 になることを確認します。3 + 0.3 + 0.12 + 0.28 = 1

はい、足して1になるので、正しいようです。

友人と乱数

ここでは、条件付き確率のまったく異なる例を紹介します。

4 人の友人 (Alex、Blake、Chris、Dusty) が、それぞれ 1 から 5 までの乱数を選びます。

友人を一人ずつ追加していきましょう。

まず、アレックスとブレイクが同じ数字を持つ確率は？

ブレイクは自分の数字とアレックスの数字を比べます。

樹形図としては、

注：「はい」と「いいえ」を合わせると1になります
(1/5 + 4/5 = 5/5 = 1)

次に、クリスを入れてみましょう・・・。

しかし、考慮すべき2つのケースがあります。

• AlexとBlakeが一致した場合、Chrisが比較する数字は1つだけです。
• しかし、AlexとBlakeが一致しなかった場合、Chrisが比較する数字は2つです。

そして、次のようになります。

一番上の行 (Alex と Blake が一致した) では、すでに一致しています (確率は 1/5)。

しかし、「AlexとBlakeがマッチしなかった」の場合、Chrisがマッチする確率は2/5になりました（ChrisはAlexとBlakeの両方に対して自分の番号をマッチさせることができるため）。

そして、そこに至るまでにかかったチャンスを掛け合わせることで、複合的なチャンスを計算することができます:

「いいえ、いいえ」のパスをたどると……4/5の確率で「いいえ」となり、続いて2/5の確率で「はい」となります。

また、すべての確率を足しても1になることに気付きます（間違いを犯していないかどうかの良いチェックになります）。

(5/25) + (8/25) + (12/25) = 25/25 = 1

では、Dustyを含めるとどうなるでしょうか？

同じ考え方で、数が増えるだけです:

OK、これで4人の友達全員です。「はい」のチャンスを合わせると101/125になります:

答えです。 101/125