Introduction: PIDコントローラの設計

このチュートリアルでは、シンプルで汎用性の高いフィードバック補償器の構造である比例・積分・微分(PID)コントローラを紹介します。 PID制御器は非常にわかりやすく、効果的なので広く採用されています。 PID制御器の魅力の1つは，すべての技術者が微分・積分を概念的に理解しており，制御理論を深く理解していなくても制御系を実装できることである． さらに、補償器は単純であっても、システムの履歴を（統合によって）捉え、システムの将来の挙動を（微分によって）予測するという点で、かなり高度なものとなっています。 ここでは、PIDパラメータのそれぞれが閉ループシステムのダイナミクスに与える影響について説明し、システムの性能を向上させるためにPIDコントローラを使用する方法を実演します。

このチュートリアルで使用される主なMATLABコマンドは：tf , step , pid , feedback , pidtune

PID Overview

このチュートリアルでは、以下のユニティフィードバックシステムを考えます。

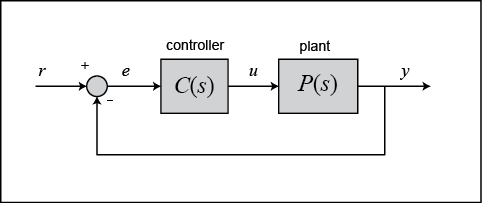
プラントへの制御入力に等しいPIDコントローラの出力は、フィードバックエラーから時間領域で次のように計算されます。

(1)$ u(t) = K_p e(t) + K_i ˶int e(t)dt + K_p ˶int e(t)dt} $

まず、PID制御器が閉ループシステムでどのように動作するかを、上に示した回路図を用いて見てみましょう。 変数($e$$r$$y$$e$）はPIDコントローラに与えられ、コントローラはこの誤差信号の時間に対する微分と積分の両方を計算します。 プラントへの制御信号($u$$K_p$$K_p$$K_i$$K_d$)に誤差の微分値をかけたものを加えたものになります。

この制御信号（$u$$y$$y$$e$）が求められます。 コントローラはこの新しいエラー信号を受け取り、制御入力の更新を計算します。 このプロセスは、コントローラが有効である間継続します。

PID制御器の伝達関数は、式(1)のラプラス変換を取ることで求められます。

(2)$ K_p + ˶ˆ꒳ˆ˵ {K_i} {s} + K_d s = ˶ˆ꒳ˆ˵ {K_d s^2 + K_p s + K_i} {s} $

ここで、$K_p$$K_i$$K_d$＝微分ゲインとなります。

MATLABでは、伝達関数モデルを直接使用して、PIDコントローラを定義することができます。 

C = pid(Kp,Ki,Kd)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 1, Ki = 1, Kd = 1 Continuous-time PID controller in parallel form.

pidオブジェクトを伝達関数に変換して、上記と同じ結果が得られることを確認してみましょう。

tf(C)
ans = s^2 + s + 1 ----------- s Continuous-time transfer function.

P、I、Dの各項の特性

比例ゲイン（$K_p$$K_p$を増加させるもう1つの効果は、定常状態の誤差をなくすことはできないものの、減少させる傾向があることです。

コントローラに微分項（$K_d$$K_p$が固定されている場合、制御が増加するのはエラーが増加した場合だけです。 微分制御では、誤差の大きさがまだ比較的小さいうちから、誤差が上向きに傾斜し始めると、制御信号が大きくなることがあります。 この期待感がシステムにダンピングを与え、オーバーシュートを減少させる傾向があります。 しかし、微分項を追加しても、定常誤差には影響がありません。

コントローラに積分項を追加すると ($K_i$)、定常誤差を減らすのに役立つ傾向があります。 安定した誤差が続くと、積分項がどんどん増えていき、制御信号が増えて誤差が減ります。 しかし、積分項の欠点は、誤差信号が符号を変えたとき、積分器が「元に戻る」までに時間がかかることがあるため、システムをより緩慢 (および振動) にする可能性があることです。

各コントローラーのパラメーター（$K_p$$K_d$$K_i$）が閉ループシステムに与える一般的な影響を以下の表にまとめました。 なお、これらのガイドラインは多くの場合に当てはまりますが、すべてではありません。 個々のゲインのチューニングの効果を本当に知りたい場合は、より多くの分析を行うか、実際のシステムでテストを行う必要があります。

tr

CL RESPONSE
RISE TIME
OVERSHOOT
SETTLING TIME
S-S ERROR
Kp
Decrease
td
Kd
変化なし

問題の例

単純なマス・スプリング・ダンパー・システムがあるとします。spring-damperシステムがあるとします。

この系の支配方程式は

(3)$ m\ddot{x}. + b\\ + kx = F $

支配方程式をラプラス変換してみると

(4)$ ms^{2}X(s) + bsX(s) + kX(s) = F(s) $

入力された力$F(s)$との間の伝達関数が と出力変位$X(s)$との間の伝達関数は次のようになります。

(5)$ ˶‾᷅˵‾᷅˵ $

Let

 m = 1 kg b = 10 N s/m k = 20 N/m F = 1 N

これらの値を上の伝達関数に代入すると

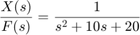
(6)$ ˶frac{X(s)}{F(s)} = ˶frac{1}{s^2 + 10s + 20} $

この問題の目的は、それぞれの項がどのようになっているかを示すことです。 $K_p$$K_i$$K_d$の各項が、以下の共通目標を得ることに貢献することです。

  • 速い立ち上がり時間
  • 最小のオーバーシュート
  • ゼロの定常誤差

オープンループ・ステップ・レスポンス

まず、オープンループ・ステップ・レスポンスを見てみましょう。 新しい m-file を作成し、以下のコードを実行します。 

s = tf('s');P = 1/(s^2 + 10*s + 20);step(P)

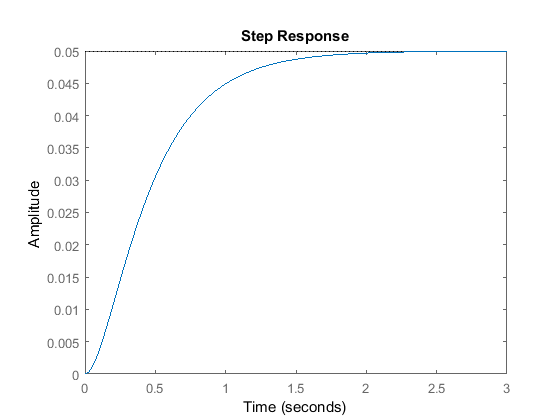
植物の伝達関数のDCゲインは1/20なので、0.05が単位ステップ入力に対する出力の最終値となります。 これは定常誤差0.95に相当し、かなり大きな値となります。 さらに、立ち上がり時間は約1秒、整定時間は約1.5秒となっています。 そこで、立ち上がり時間を短くし、整定時間を短くし、定常誤差をなくす制御器を設計してみましょう。

比例制御

上の表から、比例制御器（$K_p$）は立ち上がり時間を短くし、オーバーシュートを大きくし、定常誤差を小さくすることがわかります。

比例制御器を用いたユニティフィードバックシステムの閉ループ伝達関数は次のようになります。ここで、$X(s)$$Y(s)$$R(s)$は入力です。

(7)$ T(s)= \frac{X(s)}{R(s)} = ┄frac{K_p}{s^2 + 10s + (20 + K_p)}。 $

比例ゲイン($K_p$)を300とし、m-ファイルを以下のように変更します。ファイルを以下のように変更します。 

Kp = 300;C = pid(Kp)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp = 300 P-only controller.T = 300 ---------------- s^2 + 10 s + 320 Continuous-time transfer function.

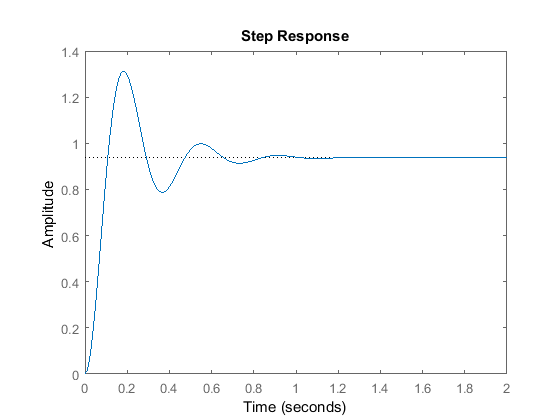
上のプロットは、比例コントローラが立ち上がり時間と定常誤差の両方を減少させ、オーバーシュートを増加させ、セトリング時間をわずかに減少させたことを示しています。

比例微分制御

ここで、PD制御について見てみましょう。 上の表から、微分制御（$K_d$）を追加することで、オーバーシュートとセトリングタイムの両方が減少する傾向にあることがわかります。 PDコントローラを用いた与えられたシステムの閉ループ伝達関数は次のとおりです。

(8)$ T(s) = ˶ˆ꒳ˆ˵ X(s)}{R(s)} = ˶ˆ꒳ˆ˵ K_d s + K_p}{s^2 + (10 + K_d) s + (20 + K_p)} $

PDコントローラを用いたシステムの閉ループ伝達関数は次のようになる。 $

先ほどと同様に$K_p$$K_d$を10とします。 以下のコマンドをmファイルに入力し、MATLABのコマンドウィンドウで実行します。 

Kp = 300;Kd = 10;C = pid(Kp,0,Kd)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = Kp + Kd * s with Kp = 300, Kd = 10 Continuous-time PD controller in parallel form.T = 10 s + 300 ---------------- s^2 + 20 s + 320 Continuous-time transfer function.

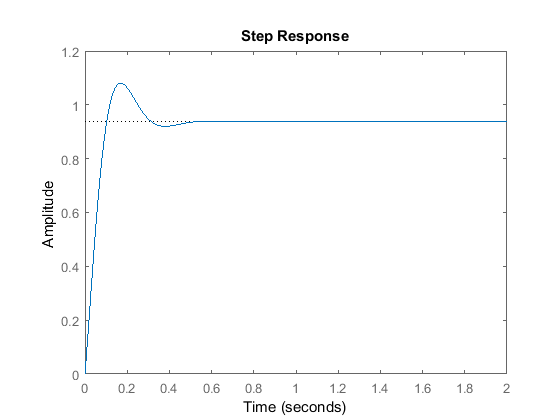
このプロットから、微分項を追加することで、オーバーシュートとセトリングタイムの両方が減少し、立ち上がり時間と定常誤差にはごくわずかな影響しかないことがわかります。

比例-積分制御

PID制御に進む前に、PI制御について調べてみましょう。 表から、積分制御（$K_i$）を追加すると、立ち上がり時間が短くなり、オーバーシュートとセトリングタイムの両方が長くなり、定常誤差が小さくなる傾向があることがわかります。 与えられたシステムでは、PIコントローラによる閉ループ伝達関数は次のようになります。

(9)$ T(s) = ˶frac{X(s)}{R(s)} = ˶frac{K_p s + K_i}{s^3 + 10 s^2 + (20 + K_p )s + K_i} $

$K_p$$K_i$を70にします。 新しいmファイルを作成し、以下のコマンドを入力します。 

Kp = 30;Ki = 70;C = pid(Kp,Ki)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- s with Kp = 30, Ki = 70 Continuous-time PI controller in parallel form.T = 30 s + 70 ------------------------ s^3 + 10 s^2 + 50 s + 70 Continuous-time transfer function.

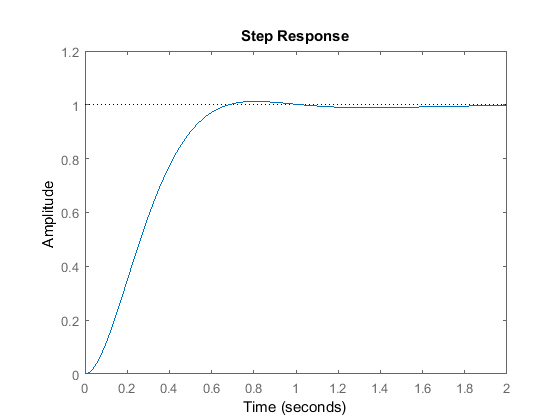
MATLABのコマンドウィンドウでこのm-fileを実行すると、上のようなプロットが生成されます。 比例ゲイン($K_p$)を下げていますが、これは積分コントローラが比例コントローラと同様に立ち上がり時間を短縮し、オーバーシュートを増加させるからです(二重効果)。 上の回答は、このケースでは積分コントローラが定常状態のエラーを解消したことを示しています。

比例-積分-微分制御

ここで、PID制御について見てみましょう。

(10)$ T(s) = ˶frac{X(s)}{R(s)} = ˶frac{K_d s^2 + K_p s + K_i}{s^3 + (10 + K_d)s^2 + (20 + K_p)s + K_i }

PID制御を用いた場合の閉ループ伝達関数は次のようになります。 $

チューニングを何度か繰り返した結果、ゲイン$K_p$$K_i$$K_d$=50で望ましいレスポンスが得られました。 確認のため、以下のコマンドをmファイルに入力し、コマンドウィンドウで実行します。 次のようなステップ応答が得られるはずです。 

Kp = 350;Ki = 300;Kd = 50;C = pid(Kp,Ki,Kd)T = feedback(C*P,1);t = 0:0.01:2;step(T,t)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 350, Ki = 300, Kd = 50 Continuous-time PID controller in parallel form.

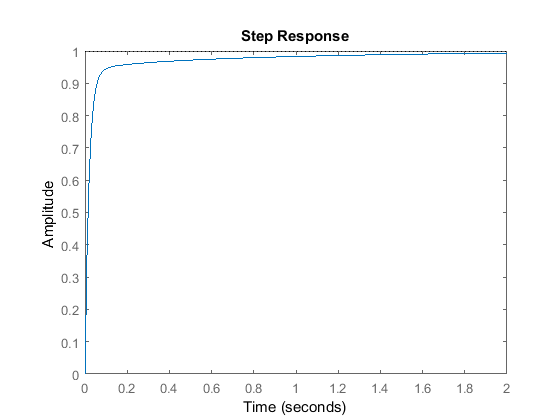
これで、オーバーシュートがなく、立ち上がりが早く、定常誤差がない閉ループシステムを設計することができました。

PIDコントローラ設計の一般的なヒント

あるシステムに対してPIDコントローラを設計する場合、望ましい応答を得るために以下に示すステップを踏んでください。

  1. 開ループ応答を得て、改善すべき点を決定する
  2. 立ち上がり時間を改善するために比例制御を追加する
  3. オーバーシュートを減らすために微分制御を追加する
  4. 定常誤差を減らすために積分制御を追加するli$K_p$$K_i$$K_d$の各ゲインを、望ましい全体的な応答が得られるまで調整します。 どのコントローラがどのような特性を制御するかは、この「PIDチュートリアル」のページで示した表をいつでも参照することができます。

最後に、必要がなければ、3つのコントローラ（比例、微分、積分）すべてを1つのシステムに実装する必要はないということを覚えておいてください。 例えば、PIコントローラが所定の要件を満たしている場合（上記の例のように）、微分コントローラをシステムに実装する必要はありません。 コントローラーはできるだけシンプルに保つようにしましょう。

実際の物理システムにおけるPIコントローラのチューニング例は、以下のリンクを参照してください。 この例では、制御の飽和、積分器の巻き上げ、ノイズの増幅など、制御を実装する上でのいくつかの課題が説明されています。

自動 PID チューニング

MATLABには、最適なPIDゲインを自動的に選択するツールが用意されており、上記のような試行錯誤のプロセスが不要になります。 チューニングアルゴリズムには、pidtuneを使って直接アクセスすることも、pidTunerを使って素敵なグラフィカルユーザーインターフェース(GUI)を介してアクセスすることもできます。

MATLABの自動チューニングアルゴリズムは、パフォーマンス(応答時間、帯域幅)とロバスト性(安定性マージン)のバランスをとるためにPIDゲインを選択します。 デフォルトでは、アルゴリズムは60度の位相マージンを設計します。

これらの自動化されたツールを試すために、まず、以下に示すコマンドを入力して、質量-バネ-ダンパーシステムの比例制御器を生成してみましょう。 表示されている構文では、Pは以前に生成されたプラントモデルで、「p」はチューナーが比例制御装置を採用することを指定しています。 

 pidTuner(P,'p')

下記のようなpidTunerのGUIウィンドウが表示されます。

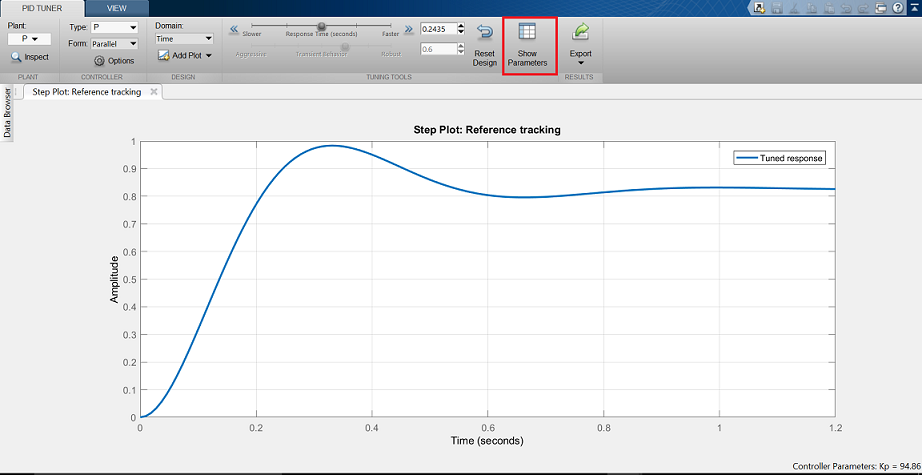
表示されているステップ応答は、私たちが手作業で設計した比例コントローラよりも遅いことに注意してください。 次に、右上の「Show Parameters」ボタンをクリックします。 予想通り、比例ゲイン $K_p$$K_p$< 300 となりました。

コントローラのパラメータをインタラクティブに調整し、その結果のレスポンスをGUIウィンドウですぐに確認できるようになりました。 下図のように、「応答時間」のスライダを右にドラッグして0.14秒にしてみてください。 これにより、応答が実際に高速化され、$K_p$が手動で選択した値に近づいていることがわかります。 また、システムの他のパフォーマンスとロバストネスのパラメータも確認できます。 スライダを調整する前は、目標とする位相余裕は60度だったことに注意してください。 これは pidTuner のデフォルトであり、一般的に堅牢性とパフォーマンスのバランスが取れています。

さて、このシステムの PID コントローラーを設計してみましょう。 前に設計したまたは(ベースライン)コントローラのCを第2パラメータとして指定することで、pidTunerは別のPIDコントローラ(PまたはPIの代わりに)を設計し、自動化されたコントローラを使用したシステムの応答をベースラインのそれと比較します。 

 pidTuner(P,C)

出力ウィンドウでは、自動化コントローラがベースラインよりも応答が遅く、オーバーシュートが多いことがわかります。 次に、ツールストリップから「Domain.Frequency」オプションを選択します。 ツールストリップから「Domain: Frequency」オプションを選択すると、周波数ドメインのチューニングパラメータが表示されます。

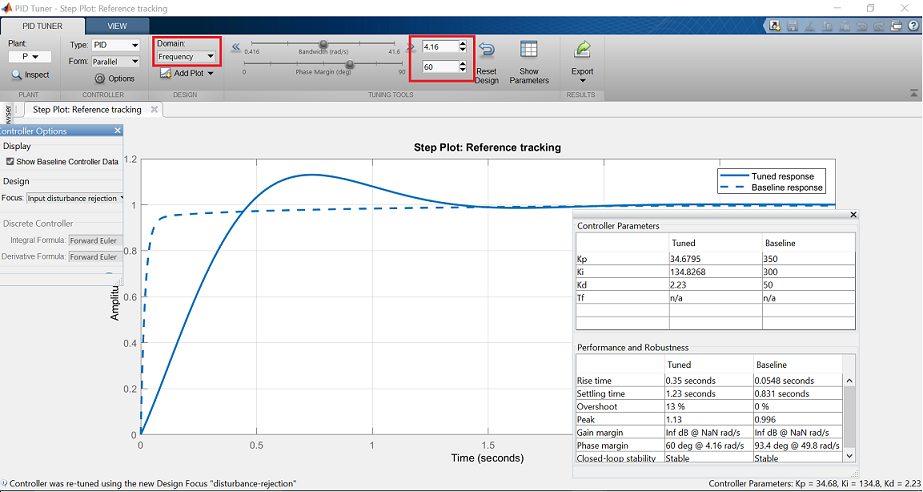
ここで、Bandwidth に 32 rad/s、Phase Margin に 90 deg を入力すると、ベースラインと同様のパフォーマンスを持つコントローラーが生成されます。 閉ループの帯域幅を大きくすると立ち上がり時間が早くなり、位相余裕を大きくするとオーバーシュートが減少してシステムの安定性が向上することに留意してください。

最後に、pidTuner GUI の代わりにコマンド ライン ツール pidtune を使用して、以下の構文で同じコントローラーを生成できることに注目してください。 

opts = pidtuneOptions('CrossoverFrequency',32,'PhaseMargin',90); = pidtune(P, 'pid', opts)
C = 1 Kp + Ki * --- + Kd * s s with Kp = 320, Ki = 796, Kd = 32.2 Continuous-time PID controller in parallel form.info = struct with fields: Stable: 1 CrossoverFrequency: 32 PhaseMargin: 90

Published with MATLAB® 9.2

MATLAB® 9.2で公開されました。

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です