こんにちは! このウェブページでは、コンピュータ サイエンスで使用される一般的なアルゴリズムの空間的および時間的な Big-O 複素数について説明します。 以前、技術面接の準備をしていたとき、質問されたときに困ってしまわないように、検索やソートのアルゴリズムの最高、平均、最悪のケースの複雑さをまとめるために、インターネットを何時間も検索していました。 ここ数年、私はシリコンバレーのスタートアップ企業や、Google、Facebook、Yahoo、LinkedIn、Uberなどの大企業で面接を受けてきましたが、面接の準備をするたびに、「なぜ誰もBig-Oのチートシートを作らないのだろう」と思っていました。 そこで、皆さんの時間を大幅に節約するために、私は先にチートシートを作成しました。 お楽しみください。 – Eric
El Graphoをチェックしてみてください。 数百万のノードとエッジをサポートするグラフ データ ビジュアライゼーション ライブラリです。Oの複雑さのチャート
Horrible |
Bad |
Fair |
Good |
Excellent |
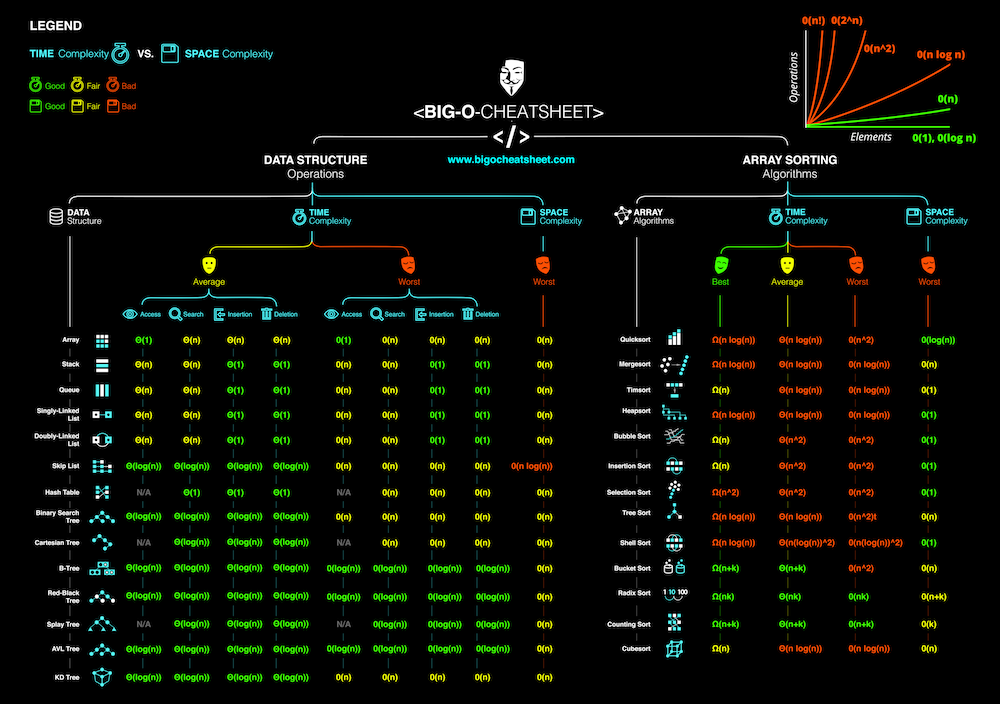
O(log n)です。 O(1) O(n) O(n log n) O(n^2) O(2^n) O(n!) 操作の要素
一般的なデータ構造の操作
| データ構造 | 時間的複雑さ | 空間的複雑さ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| アクセス | 検索 | 挿入 | 削除 | ||||||||
| アクセス | 検索 | 挿入 | 削除 | ||||||||
| アクセス | 検索 | 挿入 | 削除th | 検索 | 挿入 | 削除 | |||||
| Array | Θ(1) |
Θ(n) |
Θ(n)td |
Θ(n) |
O(1) |
O(n) |
O(n) |
O(n) |
O(n)td |
O(n) |
|
| スタック | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
||
| Queue | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
||
| Singly-…リンクリスト | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
||
| ダブリューリーリンクされたリスト | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
||
| スキップリスト | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n log(n)) |
||
| ハッシュテーブル | N/A |
Θ(1) |
Θ(1) |
Θ(1) |
N/A |
O(n) |
O(n) |
O(n) |
O(n) |
||
| バイナリーサーチツリー | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n) |
||
| カルテジアンツリー | N/A |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n))td |
N/A |
O(n) |
O(n) |
O(n) |
O(n) |
||
| B-?木 | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n))td |
O(log(n)) |
O(n) |
| 赤-。ブラックツリー | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n))td |
O(n) |
||
| プレイツリー | N/A |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
N/A |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
||
| AVLツリー | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
||
| KDツリー | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n) |
||
Array Sorting Algorithms
| Algorithm | 時間的な複雑さ | 空間的な複雑さ | ||
|---|---|---|---|---|
| ベスト | アベレージ | ワーストth | ワースト | |
| クイックソート | Ω(n log(n)) |
Θ(n log(n)) |
O(n^2) |
O(log(n)) |
| Mergesort | Ω(n log(n)) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
| Timsort | Ω(n) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
| ヒープソート | Ω(n log(n)) |
Θ(n log(n))td |
O(n log(n)) |
O(1) |
| バブルソート | Ω(n) |
Θ(n^2) |
O(n^2) |
O(1)td |
| 挿入ソート | Ω(n) |
Θ(n^2) |
O(n^2) |
O(1) |
| iv | セレクション・ソート | Ω(n^2) |
Θ(n^2) |
O(n^2) |
O(1) |
| ツリーソート | Ω(n log(n)) |
Θ(n log(n)) |
O(n^2) |
O(n) |
| シェル・ソート | Ω(n log(n)) |
Θ(n(log(n))^2) |
O(n(log(n))^2) |
O(1) |
| バケツ・ソート | Ω(n+k) |
Θ(n+k) |
O(n^2) |
O(n) |
| Radix Sort | Ω(nk) |
Θ(nk) |
O(nk) |
O(n+k) |
| カウンティング・ソート | Ω(n+k) |
Θ(n+k) |
O(n+k) |
O(k) |
| キューブソート | Ω(n) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
Learn More
- Cracking the Coding Interview: プログラミングに関する150の質問と回答
- Introduction to Algorithms, 第3版
- Data Structures and Algorithms in Java (2nd Edition)
- High Performance JavaScript (Build Faster Web Application Interfaces)
Get the Official Big-O Cheat Sheet Poster
Get the Official Big-O Cheat Sheet?Oチートシートポスター
Contributors
- Eric Rowell
- Quentin Pleple
- Michael Abed
- Nick Dizazzo
- Adam Forsyth
- Felix Zhu
- ジェイ・エンジニア
- ジョシュ・デイビス
- ノディル・トゥラクロフ
- ジェニファー・ハモン
- デビッド・ドーフマン
- Bart Massey
- Ray Pereda
- Si Pham
- Mike Davis
- mcverry
- Max. Hoffmann
- Bahador Saket
- Damon Davison
- Alvin Wan
- Alan Briolat
- Drew Hannay
- Andrew Rasmussen
- Dennis Tsang
- Vinnie Magro
- Adam Arold
- アレハンドロ・ラミレス
- アネール・ナザレス
- ラフル・チャウドリー
- ジョナサン・マッケロイ
- steven41292
- ブランドン・エイモス
- ジョエル・フリードリー
- キャスパー・ヴァン・ゲルーウェ
- エリック・ルフェーヴル-。アーダン
- オレグ
- レンフレッド・ハーパー
- パイパー・チェスター
- ミゲル・アミゴト
- アプルバ・K
- マシュー・ダロンコ
- ユン-。チェン・リン
- クレイ・タイラー
- オルハン・カン・オザルプ
- アイマン・シン
- デビッド・モートン
- オーレリアン・オームズ
- セバスティアンli Paaske Torholm
- Koushik Krishnan
- Drew Bailey
- Robert Burke
Make this page better
これらのテーブルを編集しよう!