- Behavior of the Sample Mean (x-bar)
- The Sampling Distribution of the Sample Mean
標本平均の振る舞い (x-bar)
これまで、母集団の割合であるパラメータpに対する、標本の割合である統計量p-hatの振る舞いについて説明してきました(対象となる変数がカテゴリー型の場合)。
ここからは、母平均であるパラメータμ(mu)に対する統計量x-bar(サンプル平均)の振る舞いについて見ていきます。 サンプル平均値の振る舞い
ある町のすべての赤ちゃんの出生体重が記録されています。 一度に9人の赤ちゃんの無作為なサンプルをたくさん集めた場合、サンプルの平均値はどのように振る舞うと思いますか
ここでも私たちはランダム変数を扱っています。
直観とサンプル比率の挙動について学んだことに基づいて、サンプル平均の分布について次のように予想することができます。 いくつかのサンプル平均値は低い方、例えば3,000グラム程度で、他のサンプル平均値は高い方、例えば4,000グラム程度になるでしょう。 言い換えれば、サンプルの比率の平均がpであったように、サンプル平均の平均はμ(ミュー)となります。 大規模なサンプルの場合、サンプルの平均値は3,500の母平均からあまり離れないことが予想されます。 サンプルの平均値が3,000より低かったり、4,000より高かったりすると驚くかもしれません。 小さいサンプルでは、サンプル平均が3,500からかなり離れていても、あまり驚かないでしょう。 言い換えれば、小さいサンプルではサンプル平均のばらつきが大きいと予想されます。 つまり、サンプル サイズは、サンプル比率で観察したように、サンプル平均の分布の広がりに再び役割を果たすことになります。
形状。 3,500に最も近いサンプル平均が最も一般的で、3,500から遠く離れたサンプル平均は、どちらの方向にも徐々に少なくなります。 言い換えれば、サンプル平均の分布の形は、中央が膨らみ、両端が先細りになるような、ある程度正常な形になります。
Comment:
- 繰り返しのサンプルにおけるサンプル平均 (x-bar) の値の分布は、x-bar のサンプリング分布と呼ばれます。
シミュレーションを見てみましょう。 Simulation #3 (x-bar) (4:31)
私たちがシミュレーションで見つけた結果は驚くべきものではありません。
サンプル平均のサンプリング分布
ある量的変数の値の母集団から、任意の大きさの無作為サンプルをn個繰り返して採取した場合、母平均をμ(mu)、母標準偏差をσ(sigma)とすると、すべてのサンプル平均(x-bar)の平均は母平均μ(mu)となります。
すべてのサンプル平均の広がりについては、理論的には、「サンプルが大きいほど広がりが少ない」ということよりも、はるかに正確な挙動が示されます。 実際、すべてのサンプル平均の標準偏差は、以下に示すようにサンプルサイズnに直接関係しています。
![]()
分母にサンプルサイズ n の平方根が現れるので、サンプルサイズが大きくなると標準偏差は減少します。
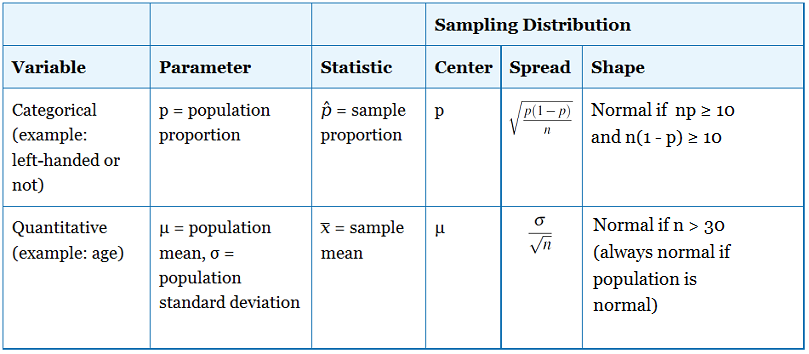
標本平均と標本比率のサンプリング分布について、今わかっていることを比較してみましょう。

ここでは、標本平均のサンプリング分布の形を調べてみます。 標本比率のサンプリング分布について説明したとき、np ≥ 10かつn(1 – p) ≥ 10の場合、この分布は近似的に正規分布であると言いました。
標本平均の分布が近似的に正規分布になるのはどのような場合でしょうか。
正規分布を持つ母集団では、非常に小さいサンプルであっても、サンプル平均が正規分布を持つことは合理的であると思われます。
母集団における変数の分布が大きく歪んでいる場合はどうなるでしょうか。 また、サンプルの平均も歪んだ分布になるのでしょうか?
次のシミュレーションでは、これらの問題を検討します。
要約すると、サンプルサイズが十分に大きい限り、サンプル平均の分布はほぼ正規になるということです。 この発見は、おそらく統計学の入門コースで提示される最も重要な結果です。
私たちは、母平均に関する結論を導き出すためにサンプル平均を使用する際、正規の確率計算を行うために、中心極限定理に何度も依存することになります。
サンプル平均が正規分布すると仮定するには、どのくらいのサンプルサイズが必要でしょうか。 シミュレーションで見たように、それは母集団の分布に依存します。
Comment:
- カテゴリー変数の場合、十分に大きな n に対してサンプル比率がほぼ正規であるという主張は、実際には中心極限定理の特別なケースです。 この場合、私たちはデータを 0 と 1 として考え、これらの 0 と 1 の「平均」は、私たちが議論した割合と等しくなります。
いくつかの例を扱う前に、標本平均と標本比例のサンプリング分布について、今わかっていることを比較対照してみましょう。
EXAMPLE 10: x-barのサンプリング分布を利用する
米国の世帯人数は、平均2.6人、標準偏差1.4人です。
(a) 無作為に選ばれた世帯が3人以上である確率は何ですか
世帯サイズの分布がかなり右に傾いているので、ここでは正規近似を使用すべきではありません。
(b) 10世帯の無作為抽出サンプルの平均サイズが3以上である確率は?
誰が見ても、10は小さなサンプルサイズです。
(c)100世帯の無作為抽出サンプルの平均サイズが3以上である確率はいくらか。
ここで、中心極限定理を援用します。世帯サイズXの分布が歪んでいても、サンプル平均世帯サイズ(x-bar)の分布は、サンプルサイズが100のように大きい場合には、ほぼ正規分布となります。 その平均値は,母集団の平均値と同じ2.そして、その標準偏差は、母集団の標準偏差をサンプルサイズの平方根で割ったものです。

求める
![]()
![]() pprobxbar2
pprobxbar2
平均値を差し引き、その結果を(サンプル平均の)標準偏差で割ることで、3をZスコアに標準化します。

3人以上の世帯はもちろんよくあることですが、100世帯のサンプルの平均サイズが3人以上であることは非常に珍しいことです。
次のアクティビティの目的は、サンプル平均(x-bar)のサンプリング分布を見つけるためのガイド付き練習を行い、x-barの特定の値を得る可能性について学ぶためにそれを使用することです。
Did I Get This?