あなたは、これらの二乗和がいったい何なのか気になっているかもしれません。 そもそもここに来たのもそれが理由かもしれません。 それは、良い線形回帰を決定するものです。
読む前に、回帰を相関と間違えていないか確認してください。
ちょっとした余談ですが、線形回帰についてもっと詳しく知りたいですか? 線形回帰について詳しく知りたい方は、説明ビデオ「The Linear Regression Model.
SST, SSR, SSE: Definition and Formulas
定義しなければならない3つの用語があります。

SSTとは
SSTと表記されるsum of squares totalは、観測された従属変数とその平均値の間の二乗された差です。
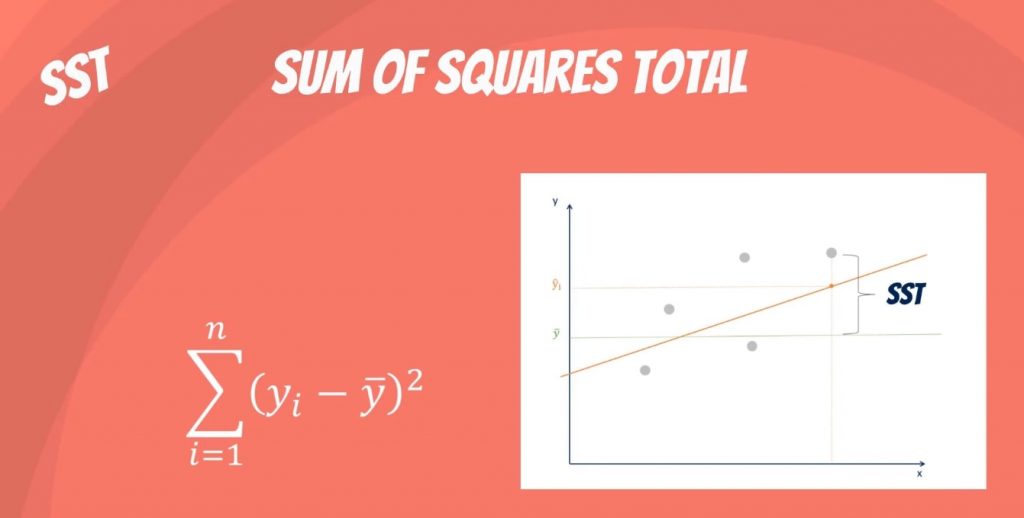
データセットの全体的な変動性の指標です。
余談ですが、SST には別の表記法があります。
SSRとは SSRとは 回帰による二乗の総和
第2項はSSRと呼ばれます。 これは、予測された値と従属変数の平均との差の合計です。

このSSRの値がsum of squares totalと等しい場合、私たちの回帰モデルは観測されたすべての変動を捉えており、完璧であることを意味します。
SSEとは
最後の項は、二乗誤差の合計、すなわちSSEです。

私たちは通常、誤差を最小化したいと考えます。 誤差が小さければ小さいほど、回帰の推定力は高くなります。 最後に、RSSまたは残差二乗和とも呼ばれていることを付け加えておきます。
異なる略語間の混乱
一部の人がSSRと表記しているため、非常に混乱しています。

いずれにしても、これらは普遍的に採用されているわけではないので、混乱は残り、それに耐えるしかありません。
2つの表記はSST、SSR、SSE、またはTSS、ESS、RSSと覚えておけばよいでしょう。

略語については対立していますが、概念やその応用については対立していません。 そこで、その点に注目してみましょう。
How Are They Related?
mathemically, SST = SSR + SSE.

根拠は次のとおりです。データセットの総変動は、回帰線によって説明される変動に、誤差と呼ばれる説明されない変動を加えたものに等しい。

全体の変動性が一定であれば、誤差が小さい方が良い回帰となります。 逆に、誤差が大きいと、回帰の力が弱くなります。 これは、どのような表記方法であっても、覚えておかなければならないことです。
次のステップ。 R-squared
さて、なぜこのような二乗和が必要なのかわからないという方のために、適切なツールをご紹介します。 それが R-squared です。 もっと詳しく知りたいですか? 線形回帰の説明力をどのように測定するかを理解するために、リンク先のチュートリアルに飛び込んでみてください!
***
もっと学びたいと思いませんか? 私たちの統計学コースで、あなたのスキルを良いものから素晴らしいものへと変えていきましょう。
Try statistics course for free
Next Tutorial: R二乗で変動性を測定する