Contents:
- Tテストとは何か?
- Tスコア
- T値とP値
- T検定の計算
- Paired T Test (Paired Samples T Test)とは
T検定とは
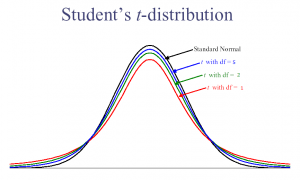
Student’s Tの様々な自由度
t検定は、グループ間の差がどれだけ有意であるかを教えてくれます; 言い換えれば、それらの差(平均値で測定)が偶然起こったものかどうかを知ることができます。
非常に簡単な例を挙げましょう。 風邪をひいて、自然療法を試してみたとします。 その風邪は2、3日続きました。 次に風邪をひいたとき、あなたは市販の医薬品を購入し、風邪は1週間続きました。 友人にアンケートを取ると、彼らは皆、ホメオパシーのレメディーを飲んだ時の方が風邪の期間が短かった(平均3日)と答えました。 あなたが本当に知りたいのは、この結果に再現性があるかどうかです。 t 検定は、2 つのグループの平均値を比較することで、これらの結果が偶然に起こる確率を知ることができます
別の例。 Student’s T-testは、平均値を比較するために実生活で使用することができます。 たとえば、製薬会社が新しい抗がん剤をテストして、それが平均寿命を向上させるかどうかを調べたいとします。 実験には、必ず対照群(プラセボ(砂糖の錠剤)を与えられた群)があります。 対照群は平均寿命が5年であるのに対し、新薬を服用した群は6年になるかもしれません。 薬が効いているのではないかと思われます。 しかし、それはたまたまかもしれません。
まだ問題がありますか?
Tスコア
Tスコアとは、2つのグループ間の差とグループ内の差の比率です。 tスコアが大きいほど、グループ間の差が大きいことを意味します。 tスコアが小さければ小さいほど、グループ間の類似性が高いことを意味します。 tスコアが3であれば、グループ間の差がグループ内の差の3倍であることを意味します。
- 大きなtスコアは、グループが異なっていることを示しています。
- 小さなtスコアは、グループが類似していることを示しています。
T-Value and P-values
“十分に大きい “とはどれくらいの大きさなのか? すべてのt-valueには、それに付随するp-valueがあります。 p値とは、サンプルデータから得られた結果が偶然に発生した確率のことです。 P値は0%から100%までの値です。 P値は通常、10進数で表記されます。 例えば、p値が5%の場合、0.05となります。 P値が低いことは良いことで、データが偶然ではなかったことを示します。 例えば、p値が0.01の場合、実験の結果が偶然である可能性が1%しかないことを意味します。 ほとんどの場合、p値が0.05(5%)であれば、そのデータは有効であると認められます。
統計量の計算・検定の種類
t検定には主に3つの種類があります:
- 独立標本のt検定は、2つのグループの平均値を比較します。
- 対の標本のt-testは、同じグループの異なる時期(例えば、1年違い)の平均を比較する。
- 1つの標本のt-testは、1つのグループの平均を既知の平均に対して検定する。
おそらく、検定を手で計算したくないでしょう(計算が非常に面倒になる可能性がありますが、どうしてもやりたい場合は、独立標本のt-testの手順をここで見つけることができます)。
以下のツールを使用して、t 検定を計算します。
How to do a T test in Excel.
T test in SPSS.
T distribution on the TI 89.
T distribution on the TI 83.
Paired T Test (Paired Samples T Test / Dependent Samples T Test)とは
Paired T test (correlated pairs t-test, paired samples t test or dependent samples t testとも呼ばれる)とは、従属的なサンプルに対してt検定を行うものです。 従属サンプルとは、基本的につながっているもので、同じ人や物についてのテストです。 例えば:
- 2つの異なる病院での膝のMRI費用
- トレーニング前とトレーニング後の同じ人に対する2つのテスト
- 異なる機器を使った同じ人に対する2つの血圧測定
。
When to choose a Paired T Test / Paired Samples T Test / Dependent Samples T Test
同じアイテム、人、または物に関する2つの測定値がある場合は、ペアのt-テストを選択します。 また、ユニークな条件で測定されている2つのアイテムがある場合にも、この検定を選択する必要があります。 例えば、Vehicle Research and Testingで車の安全性能を測定していて、車に一連の衝突テストを課しているとします。 メーカーは違いますが、同じ条件で測定していることになります。
「通常の」2標本のt検定では、2つの異なるサンプルの平均値を比較します。 例えば、2つの異なるグループのカスタマーサービス担当者にビジネス関連のテストを行ったり、2つの大学の学生に英語のスキルをテストしたりする場合です。
独立標本のt検定の帰無仮説は、μ1 = μ2です。 言い換えれば、平均値が等しいと仮定します。 対のt検定では、2つの検定の対の差が等しいというのが帰無仮説です(H0: µd = 0)。 2つの検定の違いは非常に微妙で、どちらを選択するかは、データ収集方法によります。
手書きによる一対のサンプルT検定
例題です。 以下のデータについて、手書きで対のt検定を計算します。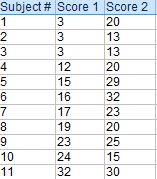
Step 1: 各Xスコアから各Yスコアを引きます。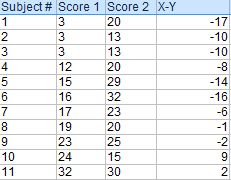
Step 2: Step 1の値をすべて加算します。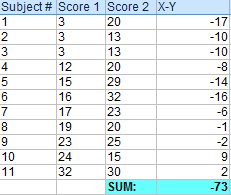
Step 3: Step 1の差を二乗します。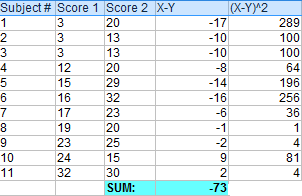
Step 4: Step 3の二乗された差をすべて加算します。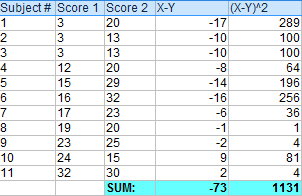
ステップ5:次の式を使ってtスコアを計算します: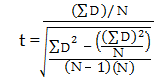
- ΣD: 差の総和(Step2のX-Yの総和)
- ΣD2:差の2乗の総和(Step4の総和)
- (ΣD)2:差の2乗の総和(Step2の総和)。
Σに慣れていない方は、先にsummation表記について読んでおくと良いでしょう。
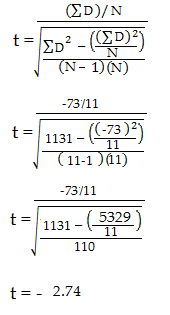
Step 6: サンプルサイズから1を引いて自由度を求めます。 11個のアイテムがあるので、11-1=10となります。
Step7:Step6の自由度を使って、t-tableでp値を求めます。 アルファレベルの指定がない場合は、0.05(5%)を使います。 この例題では、df=10の場合、t値は2.228です。
Step 8: Step 7のt表の値(2.228)と計算されたt値(-2.74)を比較します。 計算されたt値は、アルファレベル0.05の場合、表の値より大きいです。 p値はアルファレベルよりも小さい:p <.05。
注意: ±は方向を示しているので、2つのt値を比較するときにマイナス記号を無視することができ、p値はどちらの方向でも同じです。
YouTubeチャンネルでは、さらに多くの統計のヘルプやヒントをご覧いただけます!
Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York: Wiley, pp.50-55, 1956.
Stephanie Glen. “T test (Student’s T-Test): Definition and Examples” From StatisticsHowTo.com: 私たちのための初歩的な統計学です。 https://www.statisticshowto.com/probability-and-statistics/t-test/
——————————————————————————
宿題やテストの問題で助けが必要ですか? Chegg Studyでは、その分野の専門家からステップバイステップで質問に対する解決策を得ることができます。 Cheggチューターとの最初の30分は無料です。