潜在的な因果関係を調査する研究において、交絡変数とは、想定される原因と想定される結果の両方に影響を与える、測定されていない第三の変数のことです。
結果の妥当性を確保するためには、潜在的な交絡変数を考慮し、研究デザインにおいてそれらを考慮することが重要です。
交絡変数とは
交絡変数は、交絡因子または交絡要因とも呼ばれ、研究の独立変数および従属変数と密接に関連しています。
- 独立変数と相関していなければなりません。
- 従属変数と因果関係があること。
ここで、交絡変数は気温です。気温が高いと、人々はより多くのアイスクリームを食べ、より多くの時間を屋外で太陽の下で過ごし、その結果、より多くの日焼けをします。
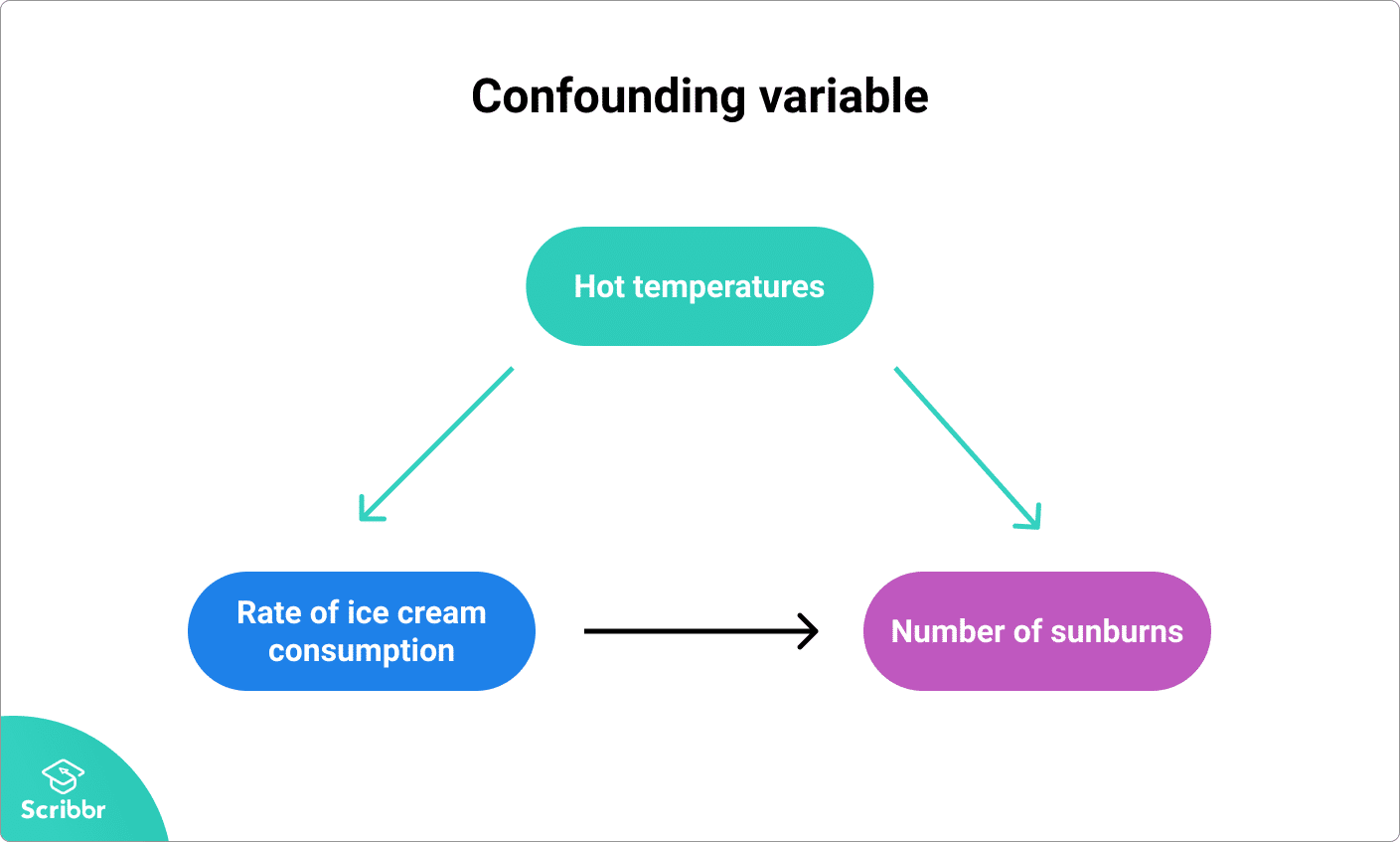

交絡変数が重要な理由
研究の内部妥当性を確保するためには、交絡変数を考慮する必要があります。 交絡変数を考慮しなければなりません。
例えば、実際には存在しない因果関係を見つけることができます。なぜなら、あなたが測定した効果は、交絡変数によって引き起こされたものであり、独立変数によって引き起こされたものではないからです。 これは、最低賃金が高いほど雇用率が高いことを意味しているのでしょうか
必ずしもそうではありません。 最低賃金が高い州の方が雇用率が高いのではなく、雇用市場が充実している州の方が最低賃金を上げる傾向にあるのかもしれません。
たとえ因果関係を正しく特定したとしても、交絡変数によって、独立変数が従属変数に与える影響を過大評価したり過小評価したりする可能性があります。
交絡変数の影響を減らす方法
交絡変数を考慮する方法はいくつかあります。 人間、動物、植物、化学物質など、どのような種類の対象を研究する場合でも、以下の方法を使用することができます。
Restriction
この方法では、潜在的な交絡因子の値が同じである被験者のみを含むことで、治療群を制限します。
これらの値は研究の対象者間で異なることはないので、独立変数と相関することはなく、研究している因果関係を混乱させることはありません。
- 比較的簡単に実施できる
- サンプルをかなり限定できる
- 他の潜在的な交絡因子を考慮できないかもしれない
マッチング
この方法では、治療群と一致する比較群を選択します。
これにより、交絡変数の違いが治療群と比較群の間の結果のばらつきの原因となる可能性を排除することができます。
低炭水化物ダイエットを行っている各被験者は、ダイエットを行っていない同じ特徴を持つ別の被験者とマッチングされます。 例えば、高学歴の40歳の男性が低炭水化物ダイエットを実践すると、高学歴の40歳の男性が低炭水化物ダイエットを実践しない場合、2人の被験者の体重減少を比較するのです。 治療サンプルの他の被験者も同じようにします。
- 制限よりも多くの被験者を含めることができます
- すべての潜在的な交絡変数で一致する被験者のペアが必要なので、実施が困難な場合があります
- 一致させることができない他の変数も交絡変数である可能性があります
統計的コントロール
すでにデータを収集している場合。 回帰モデルにコントロール変数として交絡因子の可能性を含めることができます。 こうすることで、交絡変数の影響をコントロールすることができます。
交絡の可能性のある変数が従属変数に与える影響は、回帰の結果に現れ、独立変数の影響を分離することができます。
- 実施が簡単
- データ収集後に実施可能
- 直接観察した変数しかコントロールできませんが、説明していない他の交絡変数が残っている可能性があります
無作為化
交絡変数の影響を最小化するもう一つの方法は、独立変数の値を無作為化することです。
無作為化により、十分に大きいサンプルでは、すべての潜在的な交絡変数 (研究で直接観察できないものも含む) が、異なるグループ間で同じ平均値を持つことが保証されます。
この方法では、他の方法ではほとんど不可能な、すべての潜在的な交絡変数を考慮することができるため、交絡変数の影響を軽減するための最良の方法であると考えられています。
無作為化により、治療群(低炭水化物ダイエット群)と対照群の両方が、同じ平均年齢、教育、運動レベルだけでなく、測定していない他の特性についても同じ平均値を持つことが保証されます。
- すべての可能な交絡変数を考慮することができます。 考慮することができます
- 交絡変数の影響を最小化するための最良の方法と考えられています
- 実行するのが最も困難です
- データ収集を開始する前に実施しなければなりません
- 治療群(対照群ではない)の人だけが治療を受けることを保証しなければなりません
i
交絡変数についてのよくある質問
交絡変数とは、交絡因子や混同因子とも呼ばれ、潜在的な因果関係を調べる研究における第三の変数のことです。
交絡変数は、研究の想定される原因と想定される効果の両方に関係しています。
研究デザインでは、交絡変数の可能性を特定し、その影響をどのように軽減するかを計画することが重要です。
交絡変数は、研究における独立変数と従属変数の両方と密接に関係しています。 独立変数は、想定される原因を表し、従属変数は想定される効果を表します。
交絡変数を考慮しないと、独立変数と従属変数の関係を誤って推定してしまう可能性があります。
研究の内的妥当性を確保するためには、交絡変数の影響を考慮しなければなりません。
制限では、潜在的な交絡変数の値が同じである特定の被験者のみを含めることでサンプルを制限します。
マッチングでは、治療群の被験者と比較群の被験者をマッチングさせます。
マッチングでは、治療群の被験者と比較群の被験者をマッチさせます。マッチさせた被験者は、潜在的な交絡変数の値が同じで、独立変数だけが異なります。
統計的コントロールでは、潜在的な交絡変数を回帰の変数として含めます。
無作為化では、十分に多くの被験者に治療法(または独立変数)を無作為に割り当てます。これにより、すべての潜在的な交絡変数をコントロールすることができます。
