フーリエ変換(FT)は、信号を構成する周波数に分解します。
これはどういうことでしょうか?
では、例を挙げてみましょう。 S1という信号があるとします。

この信号の強さを、ある特定の時間に測定したいとします。
つまり、信号S1の振幅は1
別の信号についても同じようにして、同じ時間を選んでその振幅を測定します。 次のような信号S2があるとします

また、信号S2の振幅は2です
さて、この2つの信号(S1とS2)を同時に発するとどうなるでしょうか。
つまり、この2つの信号を同時に発すると、この2つの信号の振幅の合計である新しい信号が得られるのです。 これは、この2つの信号が足し合わされているからです。

つまり。 S3の振幅=S1の振幅+S2の振幅=1+2=3
だから、信号S3の振幅は3
さて、面白い問題があります。
もし、信号S3だけが与えられたとすると、それは信号S1とS2の合計です。
はい、それがフーリエ変換の役目です。
この例では、フーリエ変換によって、信号S3は、信号S1とS2のような構成周波数に分解されます
しかし、元の信号をどうやって復元するのでしょうか? フーリエ変換は何をしてくれるのでしょうか?

上の写真の3つの信号をS1.S2.S3とします。
上の写真の3つの信号をS1、S2、S3とすると、これら3つの信号を合成すると赤の信号が得られますが、これは実際には3つの信号S1+S2+S3の合計です。
フーリエ変換は、一種の時間領域から周波数領域への移動です。
万が一、周波数領域から時間領域に戻りたい場合はどうすればいいのか、と疑問に思っている人がいたら、逆フーリエ変換 (IFT) を使用することで可能になります。
信号の生成と位相シフト
信号を記述するには、次の3つが必要です。
- 期間内に何回発生するかを示す信号の周波数
- 信号の高さを示す振幅
- 信号がどこから始まるかを示す位相シフト
最初に取り上げた例は非常にシンプルで、すべての信号は同じ周波数と位相差を持ち、振幅だけが異なっていました。
ここからは少し複雑な例を見ていきます。フーリエ変換をよりよく理解するためには、個々の信号を詳しく見る必要があるため、上記の例から個々の信号を見ていきます。
以下は、上で見ていた元の信号です。



の周波数です。
同じ期間、信号1にn個の波があるとすると、信号2には2n個の波があり、その逆もまた然りです。
また、実際に信号がどこから始まるかをよく見てみると 信号1は(0,0)から始まりますが、信号2は(-0.5,0)から始まることがわかります。これは、0の時点ですでに信号の最大振幅があるということです。
Amplitude(振幅)。
振幅:3つの信号はすべて異なる振幅を持ち、信号1の振幅は1、信号2と信号3の振幅はそれぞれ2と3です。
これは、エレガントで非常にシンプルな数式で表現されています。つまり、上記の例では、X軸をx、Y軸をyとすると ytの関数として、次のように生成することができます。

この式を使うと、ytの関数として生成できます。 この式を使えば、好きなタイプの信号を生成して、それらを結合して遊ぶことができます。 例えば、シグナル1、2、3を統合すると、次のようなシグナルが得られます。 次のようなシグナルが得られます。

フーリエ変換にまつわる数学
フーリエ変換の主な考え方は以下の通りです。
時間領域の任意の連続信号は、無限系列の正弦波で一意にかつ明確に表現できます。
これは何を意味するのでしょうか?
つまり、ある信号があって、その信号がある関数 x(t)f(t) を考えることができるということです。

というわけです。 信号がどんなに強くても、f(t)のように、実際に信号を完全に表現する無限系列の正弦波の合計である関数を見つけることができます。
ここで問題となるのは、上の式の係数をどのようにして見つけるかということですが、これは出力の形状、つまり信号を決定する値だからです。
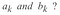
さて、これらの係数を得るためには、次のようにします。 これらの係数を得るためには、フーリエ変換を使用し、フーリエ変換から得られる結果は、係数のグループです。 そこで、X(F)を使ってフーリエ係数を表し、それは次のような積分を解くことで得られる周波数の関数です。
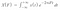
この積分でやっかいなのは、実は複素数を表すii² = -1i = √-1a + ib であることも覚えておくといいかもしれません。
また、上の積分を実際に解くと、abという複素数が得られますが、この複素数は、私たちが求めている係数に対応しています。
ただし、次の3つの問題に対処する必要があります:
iをどう扱うか。- 離散信号をどのように扱うか
では、2番目の問題から始めましょう。
離散フーリエ変換を理解するためには、まず、連続信号をどのようにサンプリングするかを理解する必要があります。
Wikipediaによると、In signal processing, sampling is the reduction of a continuous-time signal to a discrete-time signalとあります。
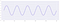
元の信号を、1秒間の振幅が2、周波数が5の信号とします。
iv
さて。 サンプリングレートを下げていくと、信号の形がどのように変化するか見てみましょう。
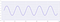
。
さらにサンプリングを減らすと、次のようになります。 を得ることができます。

div
ということで。 肝心なのは
さて、信号をサンプリングする方法がわかったところで、離散フーリエ変換と呼ばれるアルゴリズムの修正について見ていきましょう。
離散フーリエ変換
時間領域で長さNのサンプリングされた信号は、有限系列の正弦波で一意かつ明確に表現することができます。
従って、新しい定義では、もう無限を扱う必要はありません。
何が違うのでしょうか?
標準的なフーリエ変換では、連続的な信号を生成するために時間の関数x(t){x}を使用して、以下のようなサンプリングからの読み取り値を含むデータセットを作成します。

そして、離散フーリエ変換で何ができるかというと、次のようになります。 離散フーリエ変換は、{x}{X}に変換することです。

フーリエ変換の定義を見てみましょう。 {X}Xabの周波数分の成分を含んでいます。
しかし、どうして{x}{X}の2つのデータセットは同じ長さなのでしょうか?
考えてみると、{x}{X} について考えてみると、頻度とは単位時間あたりの発生数であると言いました。
つまり、非常に低いサンプリング レートで非常に高い周波数の信号があった場合、これらの信号を認識することはできません。 つまり、フーリエ変換を適用して認識できる周波数の数は、実はサンプリング レートにも左右されるのです。
さて、データセット {x}{Xk}{X} の要素であることがわかりましたが、これは次のようなフーリエ係数です。
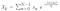
div
では、以下のようになります。 これは基本的に離散フーリエ変換です。
これで、信号をサンプリングする方法と、離散フーリエ変換を適用する方法がわかりました。 最後に、mllibsystemMLiを、オイラーの公式として知られているものを使用して取り除きたいと思います。
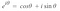
というわけです。 フーリエ変換の式にオイラーの式を入れると

また、cos(-θ) = cos(θ)sin(-θ) = -sin(θ)もわかっているので、これを上の式に使うと、次のようになります。 式は次のように簡略化できます。

となります。
そして、実は上の式を2つの和に分けることができます。 となります。

さて。 上の式を複素数の式と比較すると、a + ibとなり、対応する値は次のようになります。
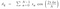
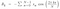
さて。 これらの値をf(t)の式に入れると、結果が得られます。
結論
実際には、高速フーリエ変換として知られる離散フーリエ変換のわずかな修正を使用します。 離散フーリエ変換は非常にシンプルで基本的なものであり、速度も遅いため、本番環境で実際に何かを行いたい場合には目的に合わないのです。 離散フーリエ変換の計算の複雑さは2次時間O(n²)O(nlogn)です。 高速フーリエ変換は、フーリエ変換のアシンメトリーを利用しています。