Mechanica van materialen
Afschuifspanningsvergelijkingen en toepassingen
Algemene afschuifspanning:
De formule om de gemiddelde afschuifspanning te berekenen is:
waarin τ = de afschuifspanning; F = de uitgeoefende kracht; A = de doorsnede van het materiaal met de oppervlakte loodrecht op de uitgeoefende krachtvector;
Straalafschuiving:
Straalafschuiving wordt gedefinieerd als de inwendige afschuifspanning van een balk veroorzaakt door de afschuifkracht die op de balk wordt uitgeoefend.
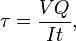waarbij V = totale afschuifkracht op de betreffende plaats; Q = statisch moment van oppervlakte; t = dikte in het materiaal loodrecht op de afschuiving; I = traagheidsmoment van de gehele dwarsdoorsnede. Deze formule is ook bekend als de Jourawski-formule.Semi-monocoque afschuivingShear spanningen binnen een semi-monocoque constructie kunnen worden berekend door de dwarsdoorsnede van de constructie te idealiseren in een geheel van langsliggers (die alleen axiale belastingen dragen) en langsliggers (die alleen afschuifstromen dragen). Door de afschuifstroom te delen door de dikte van een bepaald deel van de semi-monocoqueconstructie wordt de afschuifspanning verkregen. De maximale afschuifspanning treedt dus op in de baan met de maximale afschuifstroom of in de baan met de minimale dikte.Ook constructies in de grond kunnen bezwijken door afschuiving; bijv, het gewicht van een met aarde gevulde dam of dijk kan de ondergrond doen bezwijken, zoals bij een kleine aardverschuiving.StuikschuifspanningDe maximale schuifspanning die ontstaat in een massieve ronde staaf die aan een stoot wordt blootgesteld, wordt gegeven als de vergelijking:
waarbij U = verandering in kinetische energie; G = afschuifmodulus; V = volume van staaf; en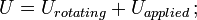 
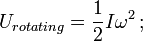
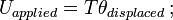
= massatraagheidsmoment; ω = hoeksnelheid.
Sheerspanning in vloeistoffen:
Alle echte vloeistoffen (vloeistoffen en gassen inbegrepen) die langs een vaste grens bewegen zullen op die grens een schuifspanning ondervinden. De glijvrijheidsvoorwaarde schrijft voor dat de snelheid van de vloeistof op de grens (ten opzichte van de grens) nul is, maar op enige hoogte van de grens moet de stroomsnelheid gelijk zijn aan die van de vloeistof. Het gebied tussen deze twee punten wordt toepasselijk de grenslaag genoemd. Voor alle Newtonse vloeistoffen in laminaire stroming is de afschuifspanning evenredig met de reksnelheid in de vloeistof waarbij de viscositeit de constante van evenredigheid is. Voor Niet-Newtoniaanse vloeistoffen is dit niet langer het geval, aangezien de viscositeit voor deze vloeistoffen niet constant is. De afschuifspanning wordt op de grens aangebracht als gevolg van dit snelheidsverlies. De afschuifspanning, voor een Newtonse vloeistof, op een oppervlakte-element evenwijdig aan een vlakke plaat, in het punt y, wordt gegeven door:
waarbij μ de dynamische viscositeit van de vloeistof is; u de snelheid van de vloeistof langs de grens; y de hoogte boven de grens. Specifiek wordt de wandschuifspanning gedefinieerd als: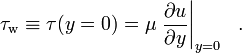 
In geval van wind wordt de afschuifspanning aan de grens windspanning genoemd.
1. Timoshenko, Stephen P. (1983), History of Strength of Material, Courier Dover Publications, p. 141, ISBN 0486611876, http://books.google.com/?id=tkScQmyhsb8C .
2. Day, Michael A. (2004), The no-slip condition of fluid dynamics, Springer Nederland, pp. 285-296, ISSN (Print) 1572-8420 (Online) 0165-0106 (Print) 1572-8420 (Online), http://www.springerlink.com/content/k1m4t1p02m778u88/.
3. Naqwi, A. A.; Reynolds, W. C. (jan 1987), “Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow”, NASA STI/Recon Technical Report N 87
4. Große, S.; Schröder, W. (2009), “Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars”, AIAA Journal 47 (2): 314-321, Bibcode 2009AIAAJ..47..314G, doi:10.2514/1.36892
5. Große, S.; Schröder, W. (2008), “Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³”, International Journal of Heat and Fluid Flow 29 (3): 830-840, doi:10.1016/j.ijheatfluidflow.2008.01.008