Objectivos de aprendizagem
Um fenómeno experimental que não podia ser adequadamente explicado pela física clássica era a radiação de corpo negro. Os objectivos para esta secção incluem
- Estar familiarizado com radiadores de corpo negro
- Aplicar a Lei Stefan-Boltmann para estimar a saída total de luz de um radiador
- Aplicar a Lei de Deslocamento de Viena para estimar o comprimento de onda de pico (ou frequência) da saída de um radiador de corpo negro
- Entender o Rayleigh-Lei de calças de ganga e como não consegue modelar correctamente a radiação de corpo negro
Toda a matéria normal a temperaturas acima de zero absoluto emite radiação electromagnética, que representa uma conversão da energia térmica interna de um corpo em energia electromagnética, e por isso é chamada radiação térmica. Inversamente, toda a matéria normal absorve a radiação electromagnética até certo grau. Um objecto que absorve TODAS as radiações que caem sobre ele, em todos os comprimentos de onda, é chamado de corpo negro. Quando um corpo negro está a uma temperatura uniforme, a sua emissão tem uma distribuição de frequência característica que depende da temperatura. Esta emissão é chamada radiação de corpo negro.
Um corpo negro à temperatura ambiente aparece negro, pois a maior parte da energia que irradia é infravermelha e não pode ser percebida pelo olho humano. Como o olho humano não consegue perceber as ondas de luz a frequências mais baixas, um corpo negro, visto no escuro à temperatura mais baixa, apenas ligeiramente visível, aparece subjectivamente cinzento, ainda que o seu espectro físico objectivo atinja picos na gama do infravermelho. Quando se torna um pouco mais quente, aparece vermelho baço. À medida que a sua temperatura aumenta, torna-se amarelo, branco, e por fim azul-branco.

A radiação de corpo negro tem um espectro de frequência característico e contínuo que, experimentalmente, depende apenas da temperatura do corpo. De facto, podemos ser muito mais precisos:
Um corpo emite radiação a uma dada temperatura e frequência exactamente assim como absorve a mesma radiação.
Esta afirmação foi provada por Gustav Kirchhoff: o ponto essencial é que se em vez disso supomos que um determinado corpo pode absorver melhor do que emite, então numa sala cheia de objectos, todos à mesma temperatura, ele absorverá melhor a radiação dos outros corpos do que irradia energia de volta para eles. Isto significa que ficará mais quente, e o resto da sala ficará mais frio, contradizendo a segunda lei da termodinâmica. Assim, um corpo deve emitir radiação exactamente da mesma forma que absorve a mesma radiação a uma dada temperatura e frequência, a fim de não violar a segunda lei da termodinâmica.
Um corpo a qualquer temperatura acima de zero absoluto irradiará até certo ponto, a intensidade e a distribuição de frequência da radiação, dependendo da estrutura detalhada do corpo. Para começar a analisar a radiação de calor, precisamos de ser específicos sobre o corpo a irradiar: o caso mais simples possível é um corpo idealizado que é um absorvedor perfeito, e portanto também (a partir do argumento acima) um emissor perfeito. Então, como construir um absorvedor perfeito no laboratório? Em 1859 Kirchhoff teve uma boa ideia: um pequeno buraco na lateral de uma caixa grande é um excelente absorvedor, uma vez que qualquer radiação que atravesse o buraco salta por dentro, muito sendo absorvida em cada ressalto, e tem poucas hipóteses de voltar a sair. Portanto, podemos fazer isto ao contrário: ter um forno com um pequeno buraco no lado, e presumivelmente a radiação que sai do buraco é tão boa representação de um emissor perfeito como vamos encontrar (Figura 2).
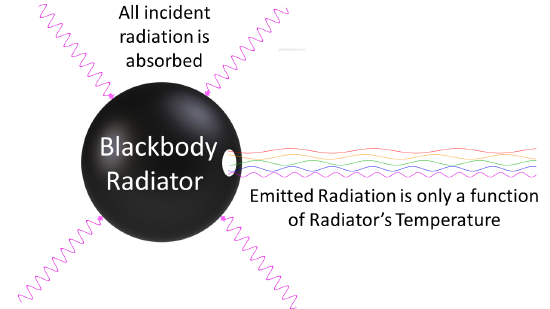
Nos anos 1890, as técnicas experimentais tinham melhorado o suficiente para que fosse possível fazer medições bastante precisas da distribuição de energia da radiação de corpo negro. Em 1895, na Universidade de Berlim, Wien e Lummer fizeram um pequeno buraco na lateral de um forno completamente fechado, e começaram a medir a radiação que saía. O feixe que saía do buraco era passado através de uma grade de difracção, que enviava os diferentes comprimentos de onda/frequências em diferentes direcções, tudo em direcção a um ecrã. Um detector foi movido para cima e para baixo ao longo do ecrã para descobrir quanta energia radiante estava a ser emitida em cada gama de frequências. Encontraram uma curva de intensidade/frequência de radiação próxima das distribuições na Figura \PageIndex{3}}.
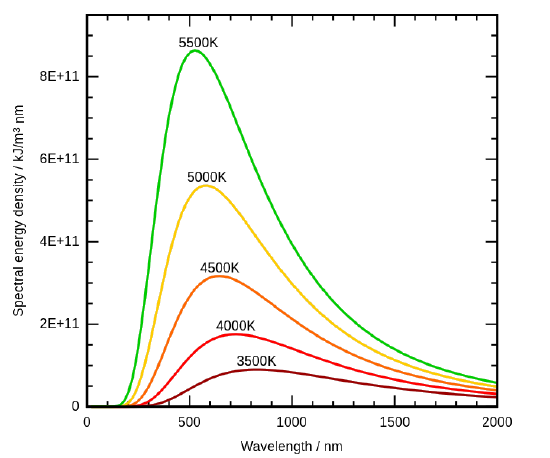
Ao medir as curvas de emissão de corpo negro a diferentes temperaturas (Figura \PageIndex{3}), foram também capazes de construir duas importantes Leis fenomenológicas (i.e, formuladas a partir de observações experimentais, não a partir de princípios básicos da natureza): Lei de Stefan-Boltmann e Lei de Deslocação de Viena.
Nem todos os radiadores são radiadores de corpo negro
A radiação de um radiador de corpo negro é produzida pela actividade térmica do material, não pela natureza do material, nem pela forma como este se excitou termicamente. Alguns exemplos de corpos negros incluem lâmpadas incandescentes, estrelas e tampos de fogão quentes. A emissão aparece como um espectro contínuo (Figura \PageIndex{3}) com múltiplas cores coexistentes. No entanto, nem todos os radiadores são radiadores de corpo negro. Por exemplo, a emissão de uma lâmpada de fluorescência não é uma. O espectro seguinte mostra a distribuição da luz de um tubo de luz fluorescente e é uma mistura de bandas discretas em diferentes comprimentos de onda de luz, em contraste com os espectros contínuos na figura {3}(PageIndex{3}) para radiadores de corpo negro.
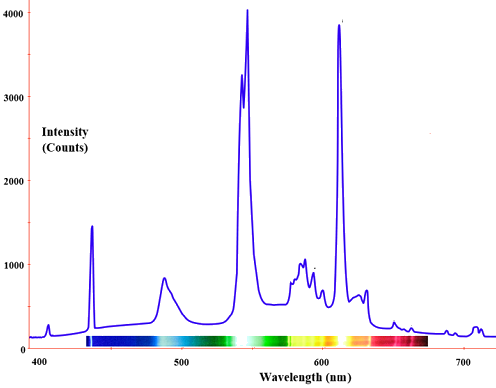
Lâmpadas fluorescentes contêm uma mistura de gases inertes (geralmente argon e néon) juntamente com uma gota de mercúrio a baixa pressão. Uma mistura diferente de cores visíveis mistura-se para produzir uma luz que nos aparece branca com diferentes sombras.
A Lei Stefan-Boltzmann
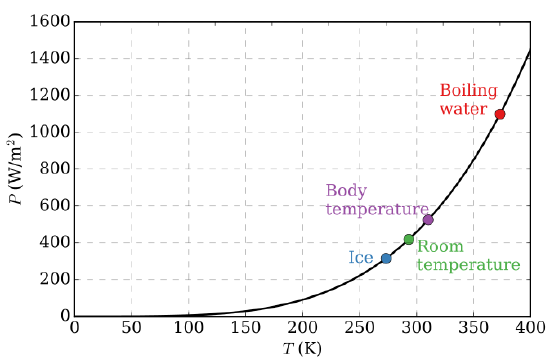
A primeira conjectura quantitativa baseada em observações experimentais foi a Lei Stefan-Boltzmann (1879) que declara a potência total (ou seja.., integrada sobre todas as frequências emissoras na Figura \PageIndex{3}) irradiada de um metro quadrado de superfície preta vai como a quarta potência da temperatura absoluta (Figura \PageIndex{4}):
p>where
- (P\) é a quantidade total de radiação emitida por um objecto por metro quadrado (Watts; m^{-2}))
li>(^sigma) é uma constante chamada constante Stefan-Boltzman (^(5.67 vezes 10 ^{-8}, Watts\\; m^{-2} K^{-4}})(T\) é a temperatura absoluta do objecto (em K)
A Lei Stefan-Boltzmann é facilmente observada através da comparação do valor integrado (ou seja sob as curvas) da distribuição experimental da radiação do corpo negro na Figura \PageIndex{3}) a diferentes temperaturas. Em 1884, Boltzmann derivou este comportamento da teoria ao aplicar o raciocínio termodinâmico clássico a uma caixa cheia de radiação electromagnética, usando as equações de Maxwell para relacionar a pressão com a densidade de energia. Ou seja, a pequena quantidade de energia a sair do buraco (Figura \PageIndex{2}) teria, claro, a mesma dependência da temperatura que a intensidade de radiação no interior.
Exemplo \(\PageIndex{1}}p>A temperatura da superfície do sol é 5700 K.
- Quanta energia é irradiada pelo sol?
- Dado que a distância à terra é de cerca de 200 raios solares, qual é a potência máxima possível de uma instalação de energia solar de um quilómetro quadrado?
Solução
(a) Primeiro, calculamos a área do sol seguida do fluxo (potência). O sol tem um raio de raio de \( 6,96 \ 96 \ 96 \ 96 \ 96 \ 96 \ 96 \ 96 \ 96 \ 96 \ 96 \ 96 \ 96 \
= 6.08 vezes 10^{18} m^2 ^2 ^end{alinhamento*}]
A energia irradiada do sol (via Lei Stefan-Boltzmann) é ^(P = ^sigma T^{4} ^).
\i&= 5,98 ^7 Watts/m^2 {alinhamento*}]
Este valor é por metro quadrado.
(b) Para calcular a potência total irradiada pelo sol é assim:
\i>>&= 3,6 ^{26} vezes 10^{26} Watts {align*}]
Lei de Deslocação de Viena
A segunda observação fenomenológica da experiência foi a Lei de Deslocação de Viena. A lei de Viena identifica o comprimento de onda dominante (pico), ou cor, da luz vinda de um corpo a uma dada temperatura. Como a temperatura do forno varia, também varia a frequência com que a radiação emitida é mais intensa (Figura \PageIndex{3}}). De facto, essa frequência é directamente proporcional à temperatura absoluta:
\\
onde a constante de proporcionalidade é \(5.879 \ ^{10} Hz/K\).
O próprio Viena deduziu esta lei teoricamente em 1893, seguindo o raciocínio termodinâmico de Boltzmann. Tinha sido observada anteriormente, pelo menos semi-quantitativamente, por um astrónomo americano, Langley. Esta mudança ascendente com o T é familiar a todos – quando um ferro é aquecido no fogo (Figura 1), a primeira radiação visível (a cerca de 900 K) é vermelho profundo, a luz visível da mais baixa frequência. Um aumento adicional em T faz com que a cor mude para laranja, depois para amarelo, e finalmente azul a temperaturas muito elevadas (10.000 K ou mais) para as quais o pico da intensidade de radiação se deslocou para além da visível para o ultravioleta.
Outra representação da Lei de Viena (Equação {Eq2}}) em termos do comprimento de onda do pico de luz é
p> onde { T} é a temperatura absoluta em kelvin e b) é uma constante de proporcionalidade chamada constante de deslocamento de Viena, igual a { 2.89 vezes 10^{-3} m, K), ou mais convenientemente para obter comprimento de onda em micrómetros, (b≈2900; μmcdot K). Esta é uma relação inversa entre o comprimento de onda e a temperatura. Portanto, quanto maior for a temperatura, menor ou menor será o comprimento de onda da radiação térmica. Quanto mais baixa a temperatura, maior ou maior o comprimento de onda da radiação térmica. Para radiação visível, os objectos quentes emitem luz mais azul do que os objectos frios.
Exemplo \(\PageIndex{2}}
Se a temperatura corporal superficial for de 90 °F.
- Quanta energia radiante em \\(W\, m^{-2}}) emitiria o seu corpo?
- Qual é o comprimento de onda de pico da radiação emitida?
- Qual é a energia radiante total emitida pelo seu corpo em Watts? Nota: O homem adulto médio tem uma área de superfície corporal de cerca de 1,9 \(m^2\) e a área média de superfície corporal para uma mulher é de cerca de 1,6 \(m^2\).
Solução
(a) 90 °F é 305 K. Usamos a Lei Stefan-Boltzmann (Equação \ref{Eq1}). A quantidade total de radiação emitida será \\( P = \sigma T^4 \).
\ &= 491 W\, m^{-2} ^{-2} ^end{align*}]
O pico do comprimento de onda da radiação emitida é encontrado usando a Lei de Viena:
\ &= \frac{ 2.898 {-3} vezes 10^{-3} m {305 K}{305 K} \\&
= 9,5 vezes 10^{-6} m = 9,5 mu mend{align*}]
A densidade total de energia radiante em Watts é :
p>>texto{Energia}_{texto feminino}_{\i1} &= (491 W\, m^{-2})(1,6 m^{2}) = 786 W {alinhamento*}]
Exemplo {PageIndex{3}): A Temperatura do Sol
Por exemplo, se o Sol tem uma temperatura de superfície de 5700 K, qual é o comprimento de onda da intensidade máxima da radiação solar?
Solução
Se substituirmos 5700 K por { T} na Equação {Eq2a}}, temos
&= 5,1 vezes 10^{-7} \m>P>Saber que a luz violeta tem um comprimento de onda de cerca de 4,0 metros, o amarelo de cerca de 5,6 metros e o vermelho de cerca de 6,6 metros, o que podemos dizer sobre a cor do pico de radiação do Sol? O comprimento de onda do pico da radiação do Sol está num comprimento de onda ligeiramente mais curto do que a cor amarela, por isso é um amarelo ligeiramente esverdeado. Para ver esta tonalidade esverdeada ao Sol, teria de se olhar para ela a partir do espaço. Acontece que a atmosfera da Terra espalha algumas das ondas mais curtas da luz solar, que muda o seu comprimento de onda de pico para amarelo puro.
Rembro que a radiação térmica abrange sempre uma vasta gama de comprimentos de onda (Figura \PageIndex{2}) e Equação \ref{Eq2a} especifica apenas o comprimento de onda único que é o pico do espectro. Assim, embora o Sol pareça branco-amarelado, quando se dispersa a luz solar com um prisma, vê-se radiação com todas as cores do arco-íris. O amarelo representa apenas um comprimento de onda característico da emissão.
Exercício \(\PageIndex{1}})
- Em que comprimento de onda é que o Sol emite a maior parte da sua radiação se tiver uma temperatura de 5,778 K?
- Em que comprimento de onda é que a Terra emite a maior parte da sua radiação se tiver uma temperatura de 288 K?
- p>Michael Fowler (Professor de Vigas, Departamento de Física, Universidade da Virgínia)
- p>David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski (“Quantum States of Atoms and Molecules”)
-
Paul Flowers (University of North Carolina – Pembroke), Klaus Theopold (University of Delaware) e Richard Langley (Stephen F. Austin State University) com autores colaboradores. O conteúdo dos livros produzidos pelo OpenStax College é licenciado sob uma licença Creative Commons Attribution License 4.0. Descarregar gratuitamente em http://cnx.org/contents/85abf193-2bd…[email protected]).
- ACuriousMind (StackExchange)
/ol> Responder a
500 nm
Responder b
10,0 microns
A Lei Rayleigh-Jeans
Lord Rayleigh e J. H. Jeans desenvolveram uma equação que explicava a radiação de corpo negro a baixas frequências. A equação que parecia expressar a radiação de corpo negro foi construída sobre todas as suposições conhecidas da física da época. A grande suposição que Rayleigh e Jean implicaram foi que quantidades infinitesimais de energia eram continuamente adicionadas ao sistema quando a frequência era aumentada. A física clássica assumiu que a energia emitida por oscilações atómicas poderia ter qualquer valor contínuo. Isto era verdade para tudo o que tinha sido estudado até esse ponto, incluindo coisas como aceleração, posição, ou energia. A sua lei Rayleigh-Jeans resultante foi
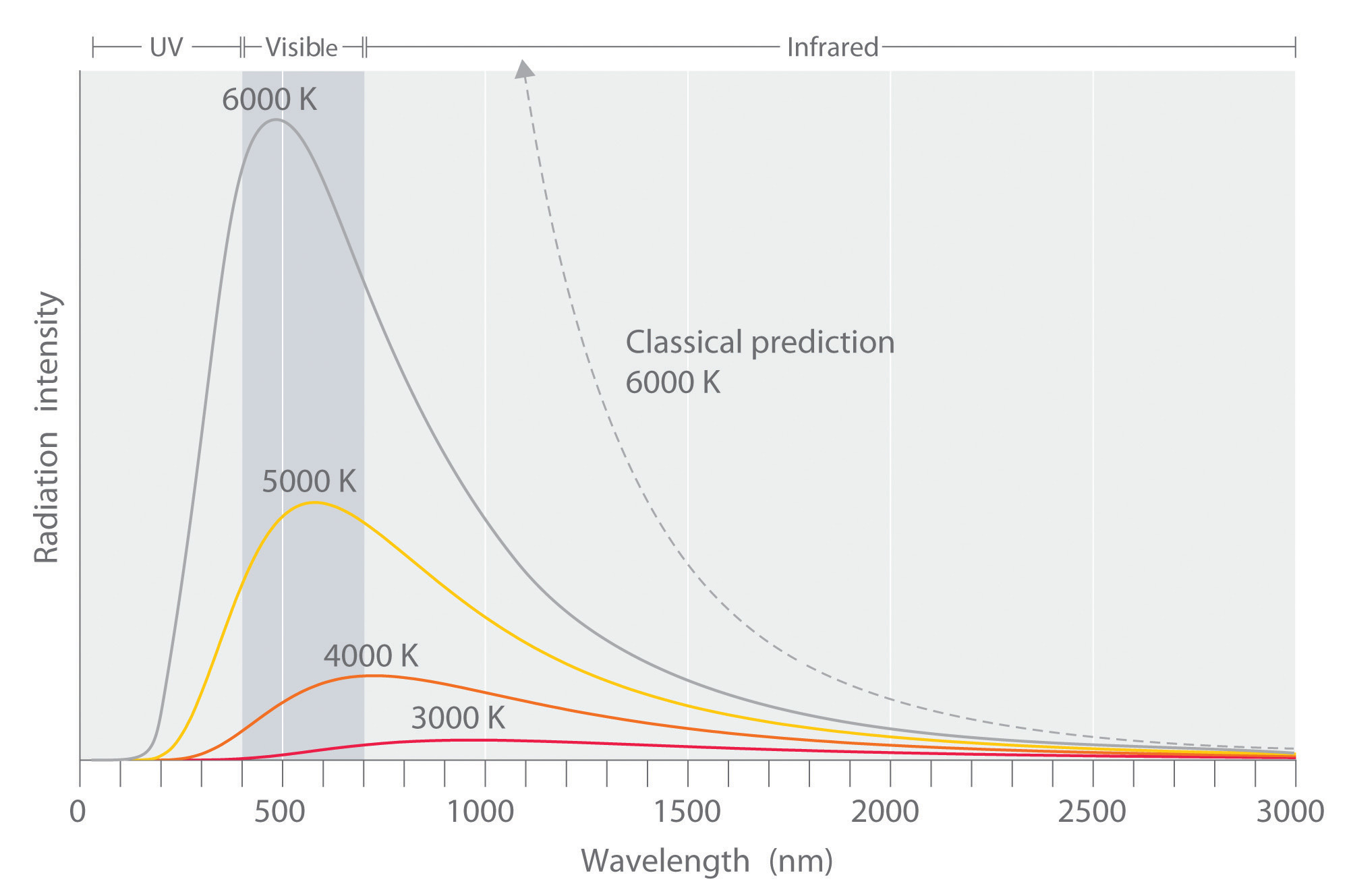
&= \dfrac{8 \pi k_B T}{c^3} \nu^2 dnu^2 dnu rótulo{Eq3} \P>P>Os dados experimentais realizados na caixa negra mostraram resultados ligeiramente diferentes dos esperados pela lei Rayleigh-Jeans (Figura {5}). A lei tinha sido estudada e amplamente aceite por muitos físicos da época, mas os resultados experimentais não mentiam, algo era diferente entre o que era teorizado e o que realmente acontece. Os resultados experimentais mostraram uma curva tipo sino, mas de acordo com a lei Rayleigh-Jeans a frequência divergiu à medida que se aproximava da região ultravioleta (Equação {Eq3}}). Ehrenfest chamou mais tarde a isto a “catástrofe ultravioleta”.
É importante enfatizar que a Equação \\(\ref{Eq3}}) é um resultado clássico: as únicas entradas são a dinâmica clássica e a teoria electromagnética de Maxwell. A carga do oscilador não aparece: o resultado é independente da força de acoplamento entre o oscilador e a radiação, o acoplamento só tem de ser suficientemente forte para assegurar o equilíbrio térmico. A derivação da lei pode ser encontrada aqui.
Representação diferencial vs. representação integral da distribuição
Radiação é entendida como uma distribuição contínua de amplitude vs. comprimento de onda ou, equivalentemente, vs. frequência (Figura \PageIndex{5}}). Numa frequência específica \(\nu), de acordo com a lei Rayleigh-Jeans, a radiação é
>p>>p> Na prática, é difícil medir uma única frequência e estamos mais interessados em intervalos de frequência. Uma frequência exacta é o limite de uma sequência de intervalos cada vez mais pequenos. Se fizermos a suposição de que, para um intervalo suficientemente pequeno, \(ρ(\nu,T)\) não varia, obtemos a sua definição para o diferencial \(dρ(ν,T)\) em Equation \ref{Eq3}:
A suposição é justa devido à continuidade de \(ρ(\nu,T)\). Esta é a aproximação de um integral num intervalo muito pequeno (dnu) pela altura de um ponto dentro deste intervalo (8pi k_bTnu^2}{c^3}) vezes o seu comprimento (dnu)). Assim, se somarmos uma quantidade infinita de pequenos intervalos como o acima, obtemos um integral. A radiação total entre o {\nu_1} e o {\nu_2} será:
p>p>p>Observe que o {\nu,T)} é quadrático em {\nu,T}).
Exemplo \PageIndex{4}: a catástrofe ultravioleta
Qual é a radiância espectral total de um radiador que segue a lei Rayleigh-Jeans para o seu espectro de emissão?
Solução
A radiância espectral total \(\rho_{tot}(T)\) é a emissão combinada sobre todos os comprimentos de onda possíveis (ou equivalente, frequências), que é uma parte integrante sobre a distribuição relevante (Equação \ref{Eq3} para a Lei Rayleigh-Jeans).
\i>>&
= \int_0^^\infty \i k_B T}{c^3} \nu^2 d\nu {alinhamento*}]
mas a integral
p>>p>p> não converge. Pior, é infinito,
Hence, a lei Rayleigh-Jeans classicamente derivada prevê que o brilho de um corpo negro é infinito. Uma vez que a radiância é potência por ângulo e área unitária, isto também implica que a potência total e, consequentemente, a energia que um corpo negro emite é infinita, o que é manifestamente absurdo. A isto chama-se a catástrofe ultravioleta porque a previsão absurda é causada pela lei clássica que não prevê correctamente o comportamento em frequências altas/comprimentos de onda pequenos (Figura \PageIndex{5}).