Guinguette Marais Poitevin

O Método 3-4-5 Para Cantos Quadrados

Por Robert Robillard em Reparação e Remodelação Doméstica

3-4-5 Método Triângulo

A carpintaria não é uma ciência exacta; é uma abordagem pragmática à resolução de problemas, construção, e reparação. A minha experiência ensinou-me que alguns princípios básicos nos guiam sobre o que irá ou não funcionar. Plumb, Level, and Square é alguns desses princípios.

3-4-5 Rule To Ensure Square Layouts

Carpenters and builders often use the 3-4-5 method for squaring cantos e assegurar que os projectos que estão a construir têm um ângulo preciso de 90 graus.

No mundo residencial e da construção, os carpinteiros usam frequentemente quadrados de velocidade e quadrados de enquadramento para verificar layouts.

Quando o layout é grande, estes quadrados de enquadramento são simplesmente demasiado pequenos para garantir a precisão necessária. Grandes projectos de remodelação e construção tais como a colocação da fundação de uma casa ou muros empregam frequentemente uma técnica de triângulo 3-4-5 para garantir ângulos precisos de 90 graus.

Evite Erros de Composição

Não importa em que projecto trabalhe se a sua base ou fundação não estiver nivelada, prumo, e quadrada o resto do seu projecto estará desligado. Os erros na base de um deck, casa ou alpendre continuarão a crescer e a compor-se quando chegar aos acabamentos, armários, ou quando chegar à armação do telhado.

3-4-5 Rule Layman’s Terms:

Se o lado curto do triângulo for 3 pés, e a perna que se estende a 90 graus for 4 pés, a hipotenusa, ou a perna mais longa, será de 5 pés.

Esta técnica requer simplesmente que o carpinteiro crie um triângulo no canto das linhas que devem ser quadradas (90 graus) uma à outra.

O triângulo 3-4-5 deve ter

• Um lado (perna triangular) com 3 pés de comprimento
• Um segundo lado (perna triangular) com 4 pés de comprimento
• Um terceiro lado, ligando as duas pernas com 5 pés de comprimento

Um triângulo com lados de 3, 4, e 5 pés terá um ângulo de 90 graus em frente do lado de 5 pés. A beleza e simplicidade desta técnica são se o carpinteiro ou construtor precisar de aumentar a precisão em paredes ou estruturas maiores, qualquer múltiplo da regra 3-4-5 pode ser implantado.

Exemplos da regra 3-4-5

• 3-4-5
• 6-8-10
• 9-12-15
• 12- 16-20
• 15-20-25

Por que é que isto funciona?

Matematicamente, porque é que o método 3-4-5 para os cantos quadrados cria um ângulo recto perfeito?

Na Geometria, um método bem conhecido de construção do ângulo recto é empregar o Teorema de Pitágoras. O matemático, Pitágoras, descobriu uma relação entre os lados de qualquer triângulo direito que é agora conhecido como o Teorema de Pitágoras. Pitágoras provou que o quadrado do lado mais comprido (a hipotenusa) é igual à soma dos quadrados dos dois lados restantes.

Esta é escrita como a seguinte equação:

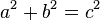
A e B são as duas pernas do triângulo direito e C é a hipotenusa. Se substituirmos os números de um triângulo 3-4-5 por esta fórmula, temos então 9″ + 16″ = 25″

Recordar o 3-4-5

Usar dimensões triangulares de 3, 4, e 5 é fácil de recordar e de aplicar. Não há equações difíceis de lembrar e o método 3-4-5 produzirá sempre um ângulo recto perfeito muito tempo.