Fórmula de velocidade média é usada para encontrar a taxa uniforme que envolve algo a viajar a um ritmo fixo e constante.
Por exemplo, Um carro viaja 3 horas. Viaja 30 milhas na primeira hora, 45 milhas na segunda hora e 75 milhas na terceira hora.
Velocidade na primeira hora = 30 milhas / hora
Velocidade na segunda hora = 45 milhas / hora
Velocidade na terceira hora = 75 milhas / hora
Temos três velocidades diferentes na viagem de três horas.
Se quisermos encontrar a velocidade média para toda a viagem de três horas, temos de encontrar a relação entre a distância total percorrida e o tempo total tomado.
Isto é, velocidade constante = (30 + 45 + 75) / 3
= 150 / 3
= 50 milhas / hora
Baseado no exemplo acima, a fórmula é para encontrar a velocidade média é dada abaixo.
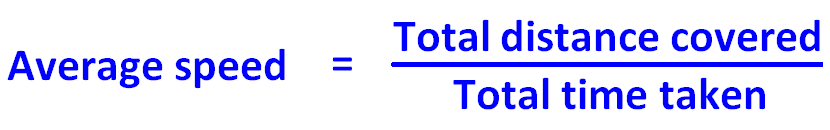
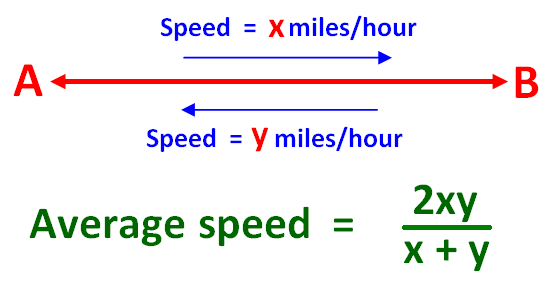
Se uma pessoa viaja de A a B a alguma velocidade, diga “x” milhas por hora. Volta de B para A a uma velocidade diferente, digamos “y” milhas por hora. Em ambos os sentidos, ele cobre a mesma distância, mas a velocidades diferentes.
Então, a fórmula é para encontrar a velocidade média para toda a viagem é dada abaixo.
Fórmula de velocidade média – Exemplos
Exemplo 1 :
David conduziu durante 3 horas a uma taxa de 50 milhas por hora, durante 2 horas a 60 milhas por hora e durante 5 horas a uma taxa de 70 milhas por hora. Qual foi a sua velocidade média para toda a viagem?
Resposta :
Passo 1 :
Fórmula para velocidade média é
= Distância total / Tempo total percorrido.
==Taxa ⋅ Tempo
Passo 2 :
Distância coberta nas primeiras 3 horas é
= 50 ⋅ 3
= 150 milhas
Distância coberta nas 2 horas seguintes é
= 60 ⋅ 2
= 120 milhas
Distância coberta nas últimas 5 horas é
= 70 ⋅ 5
= 350 milhas
P>Passo 3 :
Então, a distância total é
= 150 + 120 + 350
= 620 milhas
Total time is
= 3 + 2 + 5
= 10 horas
P>Passo 4 :
Assim, a velocidade média é
= 620 / 10
= 62
Assim, a velocidade média para toda a viagem é de 62 milhas por hora.
Exemplo 2 :
Jose viaja do local A para o local B a uma certa velocidade. Quando regressa do lugar B para o lugar A, a sua velocidade é de 60 milhas por hora. Se a velocidade média para toda a viagem é de 72 milhas por hora, encontre a sua velocidade quando viaja do lugar A para o B.
Resposta :
Passo 1 :
Deixe “a” ser a velocidade do lugar A para o B.
Velocidade do lugar B a A = 60 milhas/hora
Passo 2 :
Aqui, em ambos os sentidos, ele cobre a mesma distância.
Então, a fórmula para encontrar a velocidade média é
= 2xy / (x + y)
Passo 3 :
x —-> Velocidade do lugar A para B
x = a
y —-> Velocidade do lugar B até A
y = 60
P>Passo 4 :
Div>Dado : A velocidade média é de 72 milhas/hora.
(2 ⋅ a ⋅ 60) / (a + 60) = 72
120a = 72(a + 60)
120a = 72a + 4320
48a = 4320
a = 90
So, a velocidade do local A a B é de 90 milhas por hora.
Exemplo 3 :
David viaja do lugar A para colocar B a uma certa velocidade. Quando regressa do lugar B para o lugar A, aumenta a sua velocidade 2 vezes. Se a velocidade constante para toda a viagem é de 80 milhas por hora, encontra a sua velocidade quando viaja do lugar A para o lugar B.
Resposta :
Passo 1 :
Deixe “a” ser a velocidade do lugar A para o B.
Então, velocidade do lugar B para A = 2a
Passo 2 :
A distância percorrida nos dois sentidos (A para B e B para A) é a mesma.
Assim, a fórmula para encontrar a velocidade média é
= 2xy / (x + y)
Step 3 :
x —-> Velocidade do lugar A para B
x = a
y —-> Velocidade do lugar B até A
y = 2a
P>Passo 4 :
Given : Velocidade média = 80 milhas/hora
(2 ⋅ a ⋅ 2a) / (a + 2a) = 80
4a² / 3a = 80
4a / 3 = 80
a = 60
So, a velocidade do local A a B é de 60 milhas por hora.
Exemplo 4 :
Uma pessoa demora 5 horas a viajar do lugar A para o lugar B à razão de 40 milhas por hora. Volta do lugar B para o lugar A com 25% de aumento de velocidade. Encontrar a velocidade média para toda a viagem.
Resposta :
Passo 1 :
velocidade ( de A a B ) = 40 milhas/hora
velocidade ( de B a A ) = 50 milhas/hora (25% de aumento)
p>P>Passo 2 :
A distância percorrida em ambos os sentidos (de A a B e de B a A) é a mesma.
Então, a fórmula para encontrar a distância média é
= 2xy / (x + y)
Passo 3 :
x —-> Velocidade do lugar A para B
x = 40
y —-> Velocidade do lugar B até A
y = 50
Passo 4 :
velocidade média = (2 ⋅ 40 ⋅ 50) / (40 + 50)
velocidade média = 44.44
Assim, a velocidade média para toda a viagem é de cerca de 44,44 milhas/hora.
Exemplo 5 :
velocidade ( A a B ) = 20 milhas/hora,
velocidade (B a C ) = 15 milhas/hora,
velocidade (C a D ) = 30 milhas/hora
Se as distâncias de A a B, B a C e C a D forem iguais e se forem necessárias 3 horas para viajar de A a B, encontrar a velocidade média de A a D.
Resposta :
Passo 1 :
Formula para encontrar distância é
= Taxa ⋅ Tempo
Distância de A a B é
= 20 ⋅ 3
= 60 milhas
Div : A distância de A a B, B a C e C a D são iguais.
Total distância de A a D é
= 60 + 60 + 60
= 180 milhas
Passo 2 :
Formula para encontrar tempo é
= Distância / Velocidade
Tempo (A a B) = 60 / 20 = 3 horas
Tempo (B a C) = 60 / 15 = 4 horas
Tempo (C a D) = 60 / 30 = 2 horas
Tempo total retirado de A a D é
= 3 + 4 + 2
= 9 horas
passo 3 :
Formula para encontrar a velocidade média é
= Distância total / Total time
= 180 / 9
= 20
So, a velocidade média de A a D é de 20 milhas por hora.

Para obter mais problemas com a velocidade média,
Por favor clique aqui
Uma parte do material dado acima, se precisar de qualquer outro material, por favor use aqui a nossa pesquisa personalizada no google.
Se tiver algum feedback sobre o nosso conteúdo matemático, envie-nos por favor um e-mail:
Apreciamos sempre o seu feedback.
Pode também visitar as seguintes páginas web sobre diferentes coisas em matemática.
ProBLEMAS DE PALAVRAGENS
Problemas de palavras HCF e LCM
>p>Problemas de palavras em equações simples
Problemas de palavras em equações lineares
Problemas de palavras em equações quadráticas
Problemas de palavras de álgebra
Problemas de palavras em comboios
Problemas de palavras de área e perímetro
Problemas de palavras em variação directa e variação inversa
Problemas de palavras em preço unitário
Problemas de palavras sobre taxa unitária
Problemas de palavras sobre taxas de comparação
Converter problemas de palavras de unidades habituais
Converter problemas de palavras de unidades métricas
Problemas de palavras simples interesse
Problemas de palavras sobre interesse composto
Problemas de palavras sobre tipos de ângulos
Problemas de palavras de ângulos suplementares e complementares
Problemas de palavras de factos duplos
Problemas de palavras de trigonometria
Problemas de palavras de percentagem
Problemas de palavras de lucro e perda
Problemas de palavras de markup e markdown
Problemas de palavras de decimais
Problemas de palavras de fracções
Problemas de palavras em fractriões mistos
Problemas de uma palavra equação passo a passo
Problemas de palavras em desigualdades lineares
Problemas de palavras em rácio e proporção
Problemas de palavras de tempo e trabalho
Problemas de palavras em conjuntos e diagramas venn
Problemas de palavras em idades
Problemas de palavras em teorema pitagórico
Percentagem de um número de problemas de palavras
Problemas de palavras em velocidade constante
Problemas de palavras em velocidade média
Problemas de palavras na soma dos ângulos de um triângulo é 180 graus
OUTROS TÓPICOS
Atalhos de lucro e perda
Atalhos de percentagem
Atalhos de tabela de tempos
Tempo, atalhos de velocidade e distância
Ratio e atalhos de proporção
Domínio e gama de funções racionais
Domínio e gama de funções racionais com furos
Gráfico de funções racionais
Grafar funções racionais com furos
Converter a repetição de decimais para fracções
Representação decimal de números racionais
Raíz quadrada usando divisão longa
L.C.M método para resolver problemas de tempo e trabalho
Translação da palavra problemas em expressões algébricas
Remainder quando 2 power 256 é dividido por 17
Remainder quando 17 power 23 é dividido por 16
Soma dos números de três dígitos divisível por 6
Soma dos números de três dígitos divisível por 7
Soma dos números de três dígitos divisível por 8
Soma dos números de três dígitos divisível por 8
Soma dos números de três dígitos formados usando 1, 3, 4
Soma dos três números de quatro dígitos formados com dígitos não zero
Soma dos três números de quatro dígitos formados com 0, 1, 2, 3
Soma dos três números de quatro dígitos formados com 1, 2, 5, 6